
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Теорема: об определителе произведения
|
|
Опр-ль произведения двух матриц равен произведению опр-лей этих матриц. |АВ|=|А|*|В|.
Док-во: 
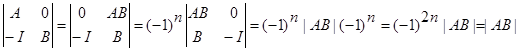
 |
14. Обратной для данной матрицы наз. матрица А-1, которая обладает след. св-вом: А*А-1=А-1*А=I
Как бы теорема (о единственности): Если для матрицы А сущ. обратная, то она единственная.
Как бы док-во: А-11, А-12 --- возможные обратные матрицы.

Как бы теорема(о вырожденной матрице): Если А---вырожденная, то обратной м-цы не существует.
Как бы док-во: Аij ---алгебраические дополнения эл-тов aij матрицы А.
Составим присоединённую м-цу 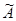 :
:
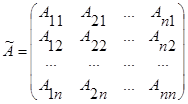 ;
; 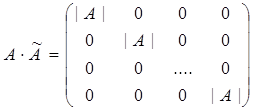 ;
; 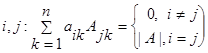
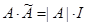 ;
; 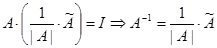
 15. Св-ва обратных матриц:
15. Св-ва обратных матриц:
1. (А-1)-1=А 2. (АВ)-1=В-1А-1 (АВ)=(В-1А-1)=А(ВВ-1)А-1=АIА-1АА-1=I
3. (Аn)-1=(А-1)n 4. (АТ)-1=(А-1)Т (АТ)(А-1)Т=(А-1А)Т=IТ=I
 |
16. Системой m линейных ур-ний с n неизвестными x1, x2,…,xn наз.
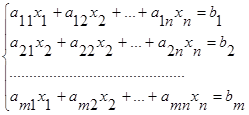 , где
, где 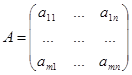 ---матрица коэффициентов системы,
---матрица коэффициентов системы,
числа aij ---коэффициенты, b1,b2,…, bn--- свободные члены, 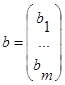 ---вектор-столбец,
---вектор-столбец, 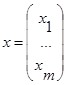
АХ=b ---краткая запись. Реш-ем с-мы наз. совокупность чисел х1=α1,х2=α2,…,хn= αn, при подстановке которых получится правильное равенство. 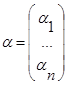 ---столбец решений.
---столбец решений.
Матричный способ решения:
А=Аnxn |A|≠0 --- невырожденная. Ах=b (2). Рассмотрим обратную матрицу А-1. Умножим обе чести равенства (2) на А-1. А-1Ах=А-1b; Ix=A-1b 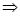 x=A-1b (3)
x=A-1b (3)
Чтобы получить решение с-мы (2) нужно умножить обратную м-цу на b. Если м-ца □ и невырожденная, то решение с-мы единственное.
 |
17. Ф-лыКрамера: 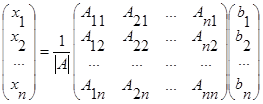 ;
;  ;
;  ;
; 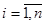 ;
;
 ---опр-ль м-цы, который получается заменой i -го столбца на столбец свободных членов.
---опр-ль м-цы, который получается заменой i -го столбца на столбец свободных членов. 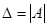
 |
18. A=Anxn. Отметим r сток и столбцов. Рассмотрим м-цу из эл-тов, находящихся на пересечении. Такая м-ца и её опр-ль наз. минором порядка r. Рангом матрицы А наз. наибольший из порядков миноров отличных от нуля. Такой минор наз. базисным. rgA ---обозначение ранга.
Св-ва ранга матрицы:
1. 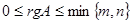 2.
2.  3.
3. 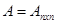 , то
, то  ---невырожденная. 4.
---невырожденная. 4. 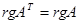
5. Если в м-це все миноры порядка k равны нулю, то все миноры более высокого порядка также равны нулю.
Док-во к 5: минор порядка k+1 разложим как опр-ль по эл-там строки. Получим с точностью до знака сумму произведений эл-тов данного минора на миноры порядка k, которые равны нулю.
 |
19. Теорема(о неизменности ранга при элементарных преобразованиях): Ранг м-цы не меняется при элементарных преобразованиях строчек и столбцов.
Док-во: 1. При перестановке миноры исходной м-цы либо не изменяются, либо поменяют знак. Тем самым все ненулевые миноры остаются ненулевыми, т. е. ранг не меняется.
2. При умножении строки м-цы на число  , миноры содержащие эту строку увеличатся в
, миноры содержащие эту строку увеличатся в 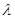 раз. Набор ненулевых миноров не изменится, и зн. сохранится ранг.
раз. Набор ненулевых миноров не изменится, и зн. сохранится ранг.
 |
20. A=Amxn u1, u2,…,un ---строчки
Данная совокупность строк наз. линейно-зависимой, если сущ. числа 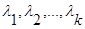 (не все=0) такие, что
(не все=0) такие, что 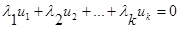 (*). Если (*) возможно только в случае
(*). Если (*) возможно только в случае 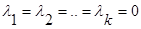 , то данный набор строк наз. линейно-независимым.
, то данный набор строк наз. линейно-независимым.
Св-ва: 1.Если в наборе есть нулевая строка, то он линейно-зависим. u1=0, u2,…, uk≠0, 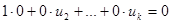 .
.
2.Если к линейно-зависимой добавить какую-либо строку, то она будет линейно-зависимой
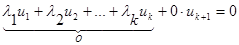
3.Если из лин.-завис. совокупности строк удалить строку, то получим линейно-независимую.
4.Если в совокупности есть одинаковые строки, то она будет линейно-зависимой
Теорема(критерий линейной зависимости): Совокупность строк линейно-зависима тогда и только тогда, когда одна из строчек явл. линейной комбинацией др. строчек.
Док-во: u1, u2,…,un --- линейно-зависимые. Покажем: u1 ---линейная комбинация др. строчек.
Действительно, сущ. 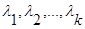
 такие что
такие что 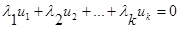
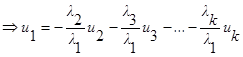 .
.
Обратно: Пусть 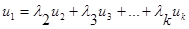 , зн.
, зн. 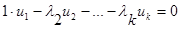
 |
21. Теорема(о базисном миноре): Строки и столбцы, на пересечении которых находятся эл-ты базисного минора, также наз. базисными. 1. Любая строка матрицы явл. линейной комбинацией базисных строчек.
2. Базисные строчки линейно-независимы.
Док-во к 1: Можно считать, что базисным явл. минор, состоящий из  , расположенный в левом верхнем углу м-цы А. В противном случае можно переставить столбцы и строки так, что эл-ты базисного минора окажутся в левом верхнем углу. rgA=const.
, расположенный в левом верхнем углу м-цы А. В противном случае можно переставить столбцы и строки так, что эл-ты базисного минора окажутся в левом верхнем углу. rgA=const.
i ---столбец j ---строка
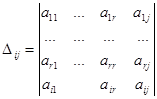 ,
, 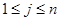 ,
, 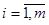 , зн.
, зн. 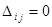 при
при 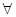 i и j.
i и j.
Если i,j>r, то 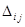 ---это минор порядка r+1, зн. =0
---это минор порядка r+1, зн. =0
Если i и/или j ≤ r, то 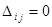 , т. к. имеются равные строки.
, т. к. имеются равные строки.
Разложим рассматриваемый опр-ль по эл-там последней строки:  , где
, где 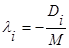 .
.
Коэффициенты 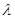 не зависят от номера строки
не зависят от номера строки 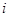 . Используя такие равенства при
. Используя такие равенства при 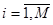 , можем записать:
, можем записать: 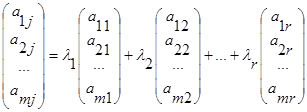 , т. е. j -тый столбец есть линейная комбинация базисных столбцов.
, т. е. j -тый столбец есть линейная комбинация базисных столбцов.
Док-во к 2: Предположим, что базисные строки линейно-зависимы, тогда одна из базисных строчек явл. линейной комбинацией др. строчек, тогда и в базисной матрице тоже самое, но в этом случае базисный минор =0, чего быть не должно.
 |
22. AX=b (1)
Теорема Кронекера-Капели: (1)---совместная, когда ранг расширенной м-цы данной с-мы = рангу м-цы коэффициентов: rg(A|b)=rgA.
Док-во:  существуют, то
существуют, то 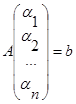 ,
, 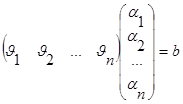 ,
,
где 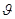 1,
1, 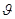 2,…,
2,…, 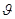 n---столбцы м-цы А. А=
n---столбцы м-цы А. А= 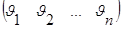
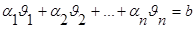 ,зн. столбец свободных членов явл. линейной комб-цией столбцов м-цы А.
,зн. столбец свободных членов явл. линейной комб-цией столбцов м-цы А.
Вычитая в (A|b) из последнего столбца соответствующую линейную комб-цию, получим (А|0). В результате ранг м-цы не меняется. rg(A|b)=rg(A|0)=rgA. Предположим rg(A|b)= rgA, зн. столбец свободных членов b не входит в число базисных столбцов расширенной м-цы. Согласно теореме о базисных минорах, столбец b явл. линейной комбинацией базисных столбцов, а зн. и всех столбцов матрицы А, т. е. 
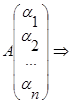 совместность системы (1)
совместность системы (1)
 |
23. Ах=0 ---однородная с-ма.
Если Ах=b в столбце b есть один ненулевой эл-т, то неоднородная. Однородная всегда совместна.
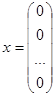 --- тривиальное решение. Остальные решения, нетривиальные.
--- тривиальное решение. Остальные решения, нетривиальные.
Теорема о сущ-нии нетривиального решения: С-ма линейных однородных ур-ний с м-цей коэффициентов mxn имеет нетривиальное решение тогда, когда rgA<n (n ---число неизвестных, Amxn).
Док-во: Пусть сущ-ет ненулевое решение  , Ах=0,
, Ах=0,
Тогда 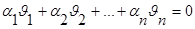 (не все
(не все 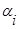 )
) 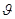 1,
1, 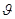 2,…,
2,…, 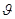 n---линейно-зависимые, не все базисные, зн. число базисных столбцов < n. rgA<n.
n---линейно-зависимые, не все базисные, зн. число базисных столбцов < n. rgA<n.
Св-ва множества решений: 1 однородная с-ма с квадратной м-цей коэффициентов имеет нетривиальное решение если она вырожденная.
2 однородная с-ма с квадратной м-цей коэффициентов имеет тривиальное решение если она невырожденная.
 |
24. Теорема о структуре общего решения с-мы линейных однородных ур-ний: Пусть A=Amxn, тогда система Ах=0 имеет n-r линейно-независимых решений, где r ---ранг м-цы А. Любое решение данной системы явл. их линейной комбинацией.
Док-во: rgA=r ---ранг. Сущ. r линейно-независимых столбцов м-цы, а остальные столбцы---их линейные комбинации. Без ограничения общности можно считать, что 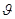 1,
1, 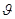 2,…,
2,…, 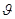 r
r 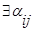 .
.
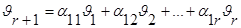

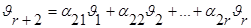

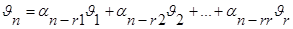
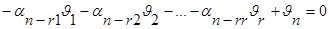
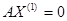
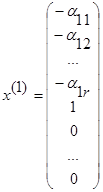
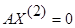
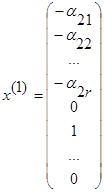

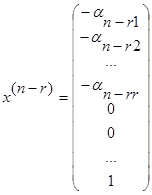
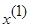 ,
,  ,…,
,…,  ---эти решения линейно-независимы если составить из них м-цу, то последние n-r строк образуют минор М:
---эти решения линейно-независимы если составить из них м-цу, то последние n-r строк образуют минор М: 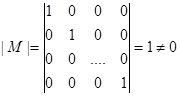
Совокупность n-r линейно-независимых решений наз. фундаментальной системой решений.
 |
25. Теорема о структуре общего решения линыйных неоднородных ур-ний: A=Amxn всякое решение неоднородной с-мы AX=b представлено так:  , где
, где 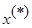 ---некоторое частное решение,
---некоторое частное решение,  ---общее решение соответствующей однородной с-мы (AX=0).
---общее решение соответствующей однородной с-мы (AX=0).
Док-во: 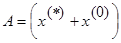
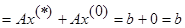 ,
, 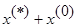 ---решение
---решение
Пусть Х ---некоторое решение, тогда AX=b (1); AX*=b (2). Вычитая (2) из (1) получим: 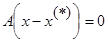
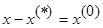 ;
;  ;
; 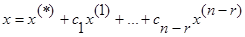
 ---фундаментальная с-ма решений
---фундаментальная с-ма решений 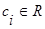
Date: 2015-09-02; view: 705; Нарушение авторских прав