Основные операции над матрицами

Определим основные операции над матрицами: сложение матриц, умножение матрицы на число и умножение матриц.

Пусть величины 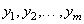выражаются через величины 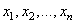при помощи линейного преобразования

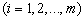, (5)

а величины 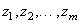— через те же величины 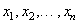при помощи преобразования

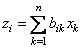
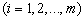. (6)

Тогда

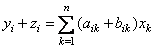
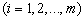. (7)

В соответствии с этим мы устанавливаем

Суммой двух прямоугольных матриц и 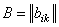одинаковых размеров 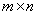называется матрица 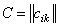тех же размеров, элементы которой равны суммам соответствующих элементов данной матрицы:

,

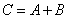если

Операция нахождения суммы данных матриц называется сложением матриц.

Пример

.

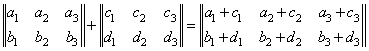Согласно определению, складывать можно только прямоугольные матрицы одинаковых размеров.

Из определения сложения матриц непосредственно следует, что эта операция обладает переместительным и сочетательным свойствами:

1° ,

2° .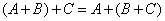

Здесь 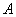, , 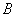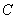— произвольные прямоугольные матрицы одинаковых размеров.

Операция сложения матриц естественным образом распространяется на случай любого числа слагаемых.

2. Умножим в преобразовании (5) величины 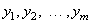на некоторое число 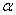из 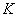. Тогда

.

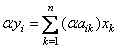
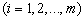В соответствии с этим имеет место

Произведением матрицы 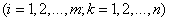на число 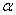из 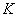называется матрица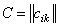 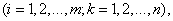элементы которой получаются из соответствующих элементов матрицы 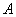умножением на число :

,

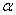если

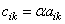
Операция нахождения произведения матрицы на число называется умножением матрицы на число.

Пример

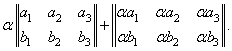
Легко видеть, что

1° ,

2° ,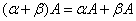

3° .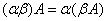

Здесь 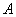, 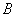— прямоугольные матрицы одинаковых размеров, 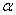, 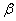— числа из поля .

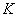Разность двух прямоугольных матриц одинаковых размеров определяется равенством

Если 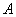— квадратная матрица порядк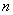а , а 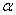— число из 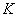, то

.

3. Пусть величины 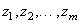выражаются через величины 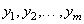при помощи преобразования

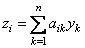
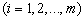(8)

а величины 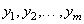— через те же величины при помощи формул

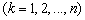. (9)

Тогда, подставляя эти выражения для 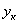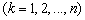в формулы (8), мы выразим 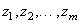через при помощи «составного» преобразования:

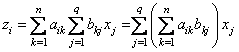
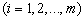. (10)

В соответствии с этим имеет место

Произведением двух прямоугольных матриц

,

называется матрица

,

у которой элемент , стоящий на пересечении 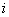-й строки и 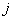-го столбца, равен «произведению» 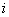-й строки первой матрицы 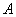на 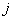-й столбец второй матрицы :

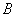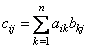
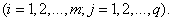
Операция нахождения произведения данных матриц называется умножением матриц.

Квадратную матрицу 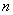-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, будем называть единичной матрицей и обозначать через 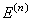или просто . Название «единичная матрица» связано со следующим свойством матрицы : для любой прямоугольной матрицы

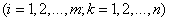
имеют место равенства

.

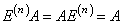Очевидно,

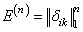
Квадратную матрицу будем называть особенной, если 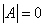. В противном случае квадратная матрица 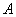называется неособенной.

Рассмотрим преобразование

.

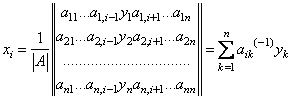
Мы получили «обратное» преобразование для матрицы A. Матрицу коэффициентов этого преобразования

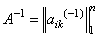
мы назовем обратной матрицей для матрицы .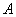

Транспонирование матрицы (обозначение: A^T) — операция, при которой матрица отражается относительно главной диагонали, то есть

Если A матрица размера , то A^T – матрица размера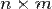

Date: 2015-09-02; view: 444; Нарушение авторских прав