Градиент функции. Производная по напрвлению

df,1 Пусть (дифференцируема в точке ), 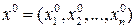. Рассмотрим прямоугольную декартовую систему координат с базисом 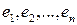. Тогда вектор, координаты которого имеют вид:

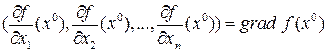- называется градиентом функции f в токе .

Пусть - ортонормированный базис прямоугольной декартовой системы координат.

Тогда 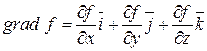. Часто используют символическую запись, вводя, векторный оператор Гамильтона (гамильтонян или набла).

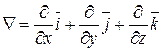, тогда (т.е. произведение числа на вектор ).

Частные производные, определенные нами ранее, можно назвать производными в направлении координатных осей.

Поставим вопрос о производных по любому фиксированному направлению.

1) Рассмотрим функцию f(x,y,z) определенную в .

2) Дан вектор .

3) .

z L

●

●

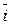
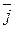y

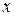
Пусть , L – прямая, 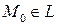, -некоторый вектор.

df.1 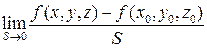, если он существует 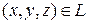называется производной f(x,y,z) в точке по направлению вектора .

Обозначение: .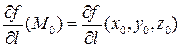

Пусть 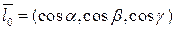- единичный вектор. - направляющие вектора, косинусы вектора .

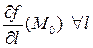Th.1 Пусть f(x,y,z) дифференцируема в точке . Тогда существует и .

Доказательство:

Очевидно, 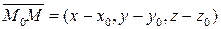, с другой стороны 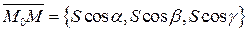, тогда:

(1)

Рассмотрим функцию 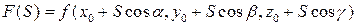, f(x,y,z) удовлетворяет теореме о производной сложной функции. Тогда, =

= .

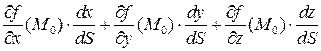Но из (1) следует 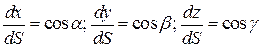, т.е. 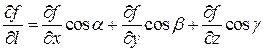= (2)

Можно записать так:

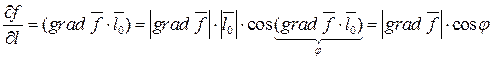(3)

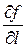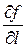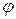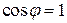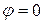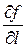Следует отметить, что не зависит от выбора системы координат. Можно показать, что наличие производных по любому направлению не является достаточным условием дифференцируемости функции f(x,y,z). Из (3) также следует, независимость от выбора системы координат (т.к. не зависит). В (3) - угол между достигает максимума при (т.е. ) т.е. при совпадении направления с направлением , причем производная в этом направлении равна 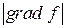. Таким образом, для дифференцируемой функции показывает направление наибыстрейшего роста функции f, причем это направление единственно.

Формальные свойства градиента:

1) ;

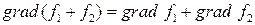2) ;

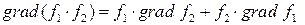3) ;

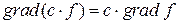4) .

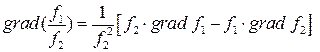df.2 Плоскость 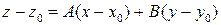называется касательной к поверхности z=f(x,y) в точке ,

.

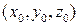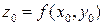
Такая плоскость для дифференцируемой в точке функции f(x,y) существует. Это следует из определения дифференцируемой функции.

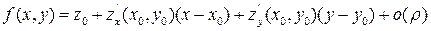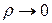
(1) , 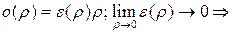касательная плоскость имеет вид:

(2)

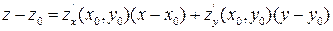
Уравнение (2) единственно, т.к. представление (1) для дифференцируемой функции единственно. При этом нормальный вектор плоскости 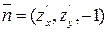из уравнения (2).

(3)

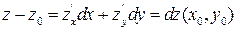
т.е. геометрический смысл дифференциала – приращение аппликаты, касательной к графику функции, при переходе от точки к точке .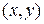

df.3 Нормалью к поверхности в точке 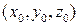называется прямая, проходящая через точку 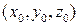перпендикулярно к касательной плоскости в этой точке, т.е. уравнение:

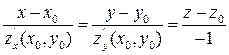(4)

Рассмотрим поверхность, заданную уравнением F(x,y,z,)=0 (5)

(где F имеет непрерывные частные производные), то считая z неявной функцией x и y и дифференцируя это равенство по x и по y, получим:

Т.е. за нормальный вектор можно взять:

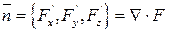
Уравнение плоскости касательной в точке 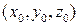имеет вид:

(6)

Следовательно, что уравнение нормали (т.е. перпендикуляра к касательной плоскости в точке 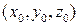) имеет вид:

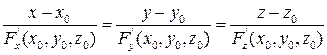(7)

Формулы (6) и (7) имеют силу лишь для неособых (ординарных) точек поверхности.

Точка 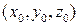поверхности F(x,y,z)=0 называется неособой, если в ней не обращаются в нуль.

Можно показать, что в достаточно малой окрестности неособой точки уравнение F(x,y,z)=0 однозначно разрешимо относительно одной из координат, причем это решение имеет непрерывные частные производные.

Date: 2015-09-02; view: 977; Нарушение авторских прав