
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Предел последовательности в
|
|
Понятие предела сформулированного в п.1 в терминах расстояния переносится естественным образом на случай  .
.
Пусть дана последовательность точек из  :
: 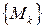 .
.
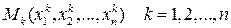 (1)
(1)
df.1 Последовательность (1) сходится к точке 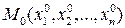 , если
, если 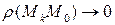 при
при  .
.
df.1’ Т.е. 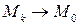 , если
, если 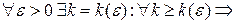
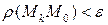
т.е. 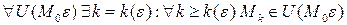 и обозначается:
и обозначается:
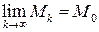
Th.1 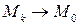 при
при 
 .
.
Доказательство:
Т.к.  и
и 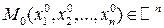 , причем между элементами:
, причем между элементами: 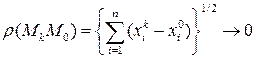 при
при 
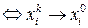 .
. 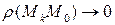 при
при  , т.е. эта метрика стремится к нулю тогда и только тогда, когда будет поэлементная сходимость.
, т.е. эта метрика стремится к нулю тогда и только тогда, когда будет поэлементная сходимость.
Из этой теоремы следует, что остаются справедливыми все теоремы в теории пределов (кроме связанных с неравенствами) для 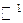 .
.
§ 3. ФУНКЦИИ НА  .
.
Пусть множество  . Нами были рассмотрены частные случаи функций.
. Нами были рассмотрены частные случаи функций.
 (1)
(1)
(1) – действительная функция (скалярная функция) векторного аргумента  .
. 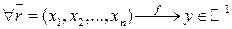 .
.
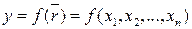

 - есть действительная функция n - действительных переменных.
- есть действительная функция n - действительных переменных.
Нам известна функция  ,
,  . Векторная функция скалярного аргумента:
. Векторная функция скалярного аргумента:
 ;
; 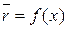
Известна функция 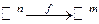 ,
, 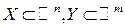 .
.
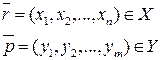
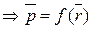 .
.
Мы будем рассматривать функции вида (1). Точка 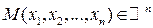 и
и 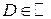 . D – область определения функции f(x).
. D – область определения функции f(x). 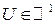 называется образом точки M, а M называется прообразом U.
называется образом точки M, а M называется прообразом U.
Множество образов обозначается f(D). Если 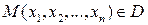 , то
, то 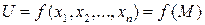 .
.
Если обозначим  , то
, то 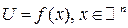 .
.
§ 4. ПРЕДЕЛ ФУНКЦИИ 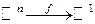 .
.
Используя понятие расстояния в  легко по аналогии с функциями одной переменной, дать определение предела функции
легко по аналогии с функциями одной переменной, дать определение предела функции 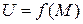 .
.
Пусть 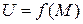 определена в
определена в 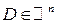 .
.
df.1 (По Гейне)
Число  называется пределом функции f в точке
называется пределом функции f в точке  , если
, если
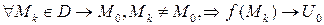 (1)
(1)
Обозначается:
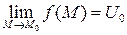 (2)
(2)
 .
.
df.2 (По Коши)
Число  называется пределом функции f в точке
называется пределом функции f в точке  , если
, если 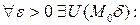
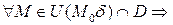
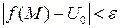 (3)
(3)
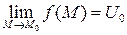 (4)
(4)
Эти два определения равносильны.
ЗАМЕЧАНИЕ.
Если n=2, т.е. рассматривается функция двух переменных и M(x,y), 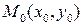 , то (2).
, то (2).
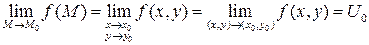
Если функция двух переменных f(x,y) определена в 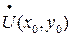 , а число
, а число  есть ее предел при
есть ее предел при 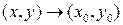 , то пишут:
, то пишут:
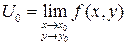
и называют иногда число  двойным пределом.
двойным пределом.
df.3 (Определение предела функции в точке)
Пусть 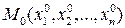 некоторая предельная точка области определения D данной функции от n -переменных.
некоторая предельная точка области определения D данной функции от n -переменных.
Число  называется пределом этой функции в точке
называется пределом этой функции в точке  , если
, если 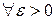
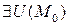 , что
, что  принадлежащих области определения функции, выполняется условие:
принадлежащих области определения функции, выполняется условие:
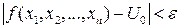 , т.е.
, т.е. 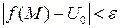
то, что функция f(M) имеет предел в точке  записывается так:
записывается так:
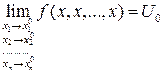
или 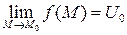 .
.
§ 5. НЕПРЕРЫВНОСТЬ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ.
Пусть  и
и 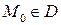
df.1 (По Гейне)
Функция f называется непрерывной в точке  , если
, если 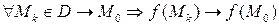 , т.е. если:
, т.е. если:
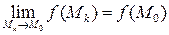 (1)
(1)
df.2 (По Коши)
Функция f называется непрерывной в точке  , если
, если 
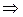
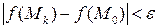 (2)
(2)
Будем обозначать непрерывность в точке  функцию так:
функцию так:
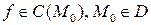
df.3 Пусть  определена в
определена в  . Полным приращением f в точке
. Полным приращением f в точке  называется:
называется:
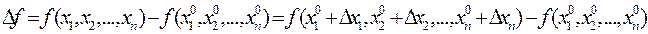
где 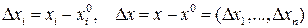 .
.
Th.1 (Непрерывность сложной функции)
Пусть 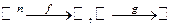 ,
, 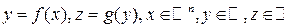 ,
,
f -непрерывна в точке  ,
, 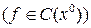 , g – непрерывна в
, g – непрерывна в  непрерывна в точке
непрерывна в точке  .
.
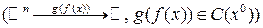 .
.
Доказательство аналогично функции одной переменной, непрерывной на сегменте. Аналогом сегмента в многомерном случае является замкнутое ограниченное множество (компакт).
Th.2 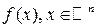 - непрерывна в точке
- непрерывна в точке 
 .
.
(Б/Д).
Или если функция  определена в некоторой окрестности точки M и непрерывна в точке M, то она непрерывна в этой точке по каждой из переменных
определена в некоторой окрестности точки M и непрерывна в точке M, то она непрерывна в этой точке по каждой из переменных  . Обратное утверждение неверно.
. Обратное утверждение неверно.
df.4 Пусть 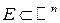 , E – компакт
, E – компакт 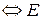 - ограничено и замкнуто в
- ограничено и замкнуто в  .
.
df.5 Пусть 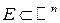 ,
,  и f(x) –непрерывна
и f(x) –непрерывна 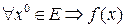 называется непрерывной на E.
называется непрерывной на E.
Обозначение: 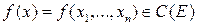 .
.
Функция f(M) называется непрерывной в точке  , если предел этой функции в точке
, если предел этой функции в точке  существует и равен частному значению
существует и равен частному значению 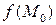 .
.
Заметим, что поскольку 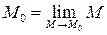 , то условие непрерывности функции
, то условие непрерывности функции  в точке
в точке  можно символически записать в виде:
можно символически записать в виде:
 , т.е. для непрерывной в точке
, т.е. для непрерывной в точке  функции символ
функции символ 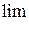 и символ f можно менять местами.
и символ f можно менять местами.
Точки пространства  , в которых функция
, в которых функция 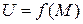 не обладает свойством непрерывности, называются точками разрыва этой функции или если функция неопределенна в точке
не обладает свойством непрерывности, называются точками разрыва этой функции или если функция неопределенна в точке  и не является в ней непрерывной, то говорят, что
и не является в ней непрерывной, то говорят, что  есть точка разрыва.
есть точка разрыва.
§ 6. СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ.
Для функций многих переменных (Ф. М. П.) справедливы основные свойства функций одной переменной, но при этом следует иметь ввиду, что многие свойства f(x) существенно зависели от области определения. Так в формулировках многих свойств существенным было то, что функция задавалась на сегменте.
I. Th.1 Пусть 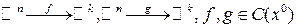 , тогда:
, тогда:
1. 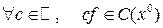 .
.
2. 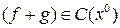 .
.
3. 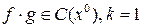 .
.
4. Если дополнительно  , то
, то 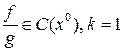
Доказательство:
Из определения непрерывности и теоремы о пределе функций этого вида.
II. Th.2 Если 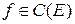 , где E – компакт, тогда она:
, где E – компакт, тогда она:
1. Ограничена на нем: 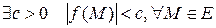 .
.
2. Принимает свое наибольшее и наименьшее значение: т.е. 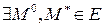 , такие, что
, такие, что  .
.
3.  , таких, что
, таких, что 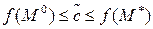
 , такая, что
, такая, что 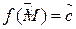 (принимает все промежуточные значения).
(принимает все промежуточные значения).
4. f в E – равномерно непрерывна, т.е. 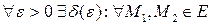 ,
,

Пусть 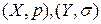 - метрические пространства,
- метрические пространства,  .
.
df. Функция 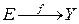 называется равномерно непрерывной на множестве E, если
называется равномерно непрерывной на множестве E, если 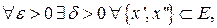
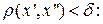
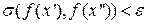 )
)
Th.3 (Теорема Вейерштрасса)
Пусть  - компакт,
- компакт, 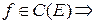 тогда f ограничена на E и достигает на E своей верхней и нижней граней (наибольшего и наименьшего значений), т.е.
тогда f ограничена на E и достигает на E своей верхней и нижней граней (наибольшего и наименьшего значений), т.е. 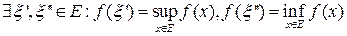 .
.
§ 7. ЧАСТНЫЕ ПРОИЗВОДНЫЕ.
Пусть в некоторой (открытой) области D имеем функцию 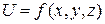 , возьмем точку
, возьмем точку 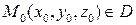 . Примем y и z за постоянные значения
. Примем y и z за постоянные значения  и будем изменять x, тогда функция U будет функцией одной переменной
и будем изменять x, тогда функция U будет функцией одной переменной 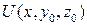 (в окрестности точки
(в окрестности точки  ). Вычислим производную этой функции в точке
). Вычислим производную этой функции в точке 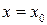 . Придадим этому значению
. Придадим этому значению  приращение
приращение 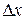 , тогда функция получит приращение:
, тогда функция получит приращение:
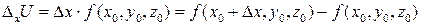 - это и есть частное приращение (по x).
- это и есть частное приращение (по x).
По определению производной, она представляет собой предел:
 - эта производная называется частной производной функции f(x,y,z) по x в точке
- эта производная называется частной производной функции f(x,y,z) по x в точке 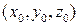 .
.
В этом определении не все координаты равноправны, т.к.  наперед фиксированы, а x меняется, стремясь к
наперед фиксированы, а x меняется, стремясь к  .
.
Частную производную обозначают одним из символов:
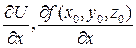 (круглым
(круглым  вместо прямого
вместо прямого  в обозначении частной производной предложил пользоваться Карл Густав Якоби (1804-1851))
в обозначении частной производной предложил пользоваться Карл Густав Якоби (1804-1851))
 .
.
Аналогично вводятся частные производные по  .
.
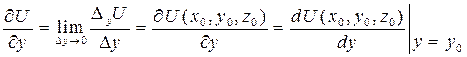 df:
df:
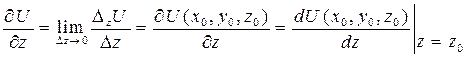 df:
df:
Где 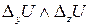 - приращения функции соответственно по переменным
- приращения функции соответственно по переменным  .
.
Изложенные рассуждения для функции 3-х переменных остаются справедливыми и для функций любого числа переменных.
Рассмотрим функцию y=f(x), где  или
или  k=1.
k=1.
Пусть f определена в некоторой окрестности точки 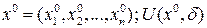 .
.
df.1 Частным приращением в точке  функции f по переменной
функции f по переменной 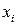 называется
называется 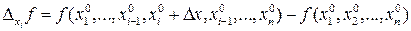 , где
, где 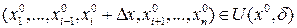 .
.
Очевидно, если все переменные за исключение 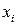 зафиксированы, то
зафиксированы, то  - есть функция одного переменного, т.е.
- есть функция одного переменного, т.е. 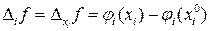 .
.
df.2 Частной производной функции f по переменной 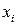 в точке
в точке  называется обычная производная функции f при всех фиксированных переменных кроме
называется обычная производная функции f при всех фиксированных переменных кроме 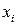 , т.е.:
, т.е.:
 , если этот предел существует. Очевидно, при n=1 это определение совпадает с определением обычной производной.
, если этот предел существует. Очевидно, при n=1 это определение совпадает с определением обычной производной.
ПРИМЕР.
 , т.е. имеем функцию двух переменных
, т.е. имеем функцию двух переменных  .
.
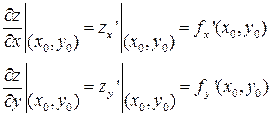
Из определения частных производных следует, что при их вычислении можно пользоваться всеми правилами вычисления обычных производных.
ПРИМЕР №1.

Решение:
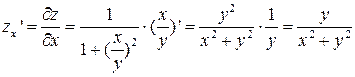
 .
.
Отметим, что при n=1 из существования производной следует непрерывность функции.
При 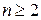 даже, если существуют все частные производные f – необязательно является непрерывной.
даже, если существуют все частные производные f – необязательно является непрерывной.
ПРИМЕР №2.
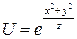
Решение:

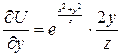
 .
.
Геометрический смысл частных производных

Выясним геометрический смысл частных производных для функции  , т.е.
, т.е.  .
.
Геометрическим изображением данной функции является некоторая поверхность S.
Полагая, y=const,  :
:
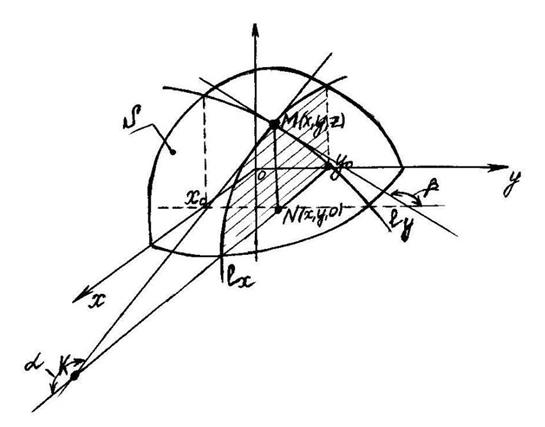
Получим некоторую плоскую кривую 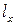 , представляющую собой сечение поверхности S соответствующей плоскостью, параллельной координатной плоскости XOZ.
, представляющую собой сечение поверхности S соответствующей плоскостью, параллельной координатной плоскости XOZ.
Пусть MK – касательная к кривой 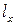 в точке M(x,y,z).
в точке M(x,y,z). 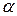 - угол, образованный этой касательной с положительным направлением оси OX.
- угол, образованный этой касательной с положительным направлением оси OX.
Т.к. 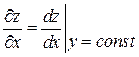 , то на основании геометрического смысла обычной производной имеем:
, то на основании геометрического смысла обычной производной имеем:
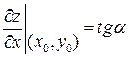
Т. о. геометрический смысл частной производной 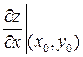 есть тангенс угла наклона, образованного касательной к кривой, лежащей в пересечении поверхности
есть тангенс угла наклона, образованного касательной к кривой, лежащей в пересечении поверхности  и плоскости
и плоскости 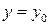 в точке
в точке 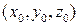 и положительным направлением оси OX.
и положительным направлением оси OX.
Аналогично, если 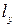 -есть сечение поверхности S плоскостью
-есть сечение поверхности S плоскостью 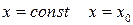 и угол
и угол 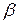 -угол, образованный с осью OY касательной ML в точке M(x,y,z) к кривой
-угол, образованный с осью OY касательной ML в точке M(x,y,z) к кривой 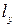 , то
, то 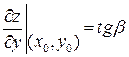 .
.
Физический смысл частной производной 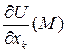 - это скорость изменения функции в точке M в направлении оси
- это скорость изменения функции в точке M в направлении оси 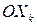 .
.
§ 8. ДИИФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ.
Пусть 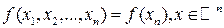 (1) определена в некоторой окрестности
(1) определена в некоторой окрестности 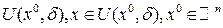 ,
, 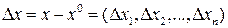 .
.
df.1 Полным приращением функции f в точке  , соответствующим приращениям
, соответствующим приращениям 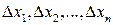 аргументов, называется выражение:
аргументов, называется выражение:
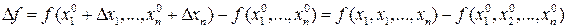
 При n=2
При n=2
y

 D
D

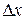
0 x
df.2 Функция  называется дифференцируемой в точке
называется дифференцируемой в точке 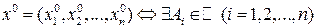 и ее полное приращение в этой точке может быть представлено в виде:
и ее полное приращение в этой точке может быть представлено в виде:
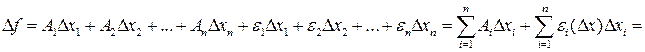
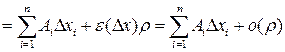 (2)
(2)
Где 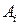 - независящее от
- независящее от 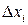 числа, а
числа, а  - бесконечно малое при
- бесконечно малое при  функции,
функции, 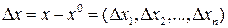 .
.
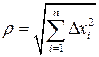 - расстояние между точками
- расстояние между точками 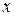 и
и  .
.
Отметим, что запись 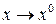 (или
(или 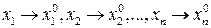 ) эквивалентна записи
) эквивалентна записи 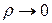 при
при 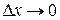 .
.
Условие (2) называется условием дифференцируемости функции в данной точке.
Если (векторная) функция f дифференцируема в точке 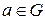 , то будем писать
, то будем писать  если
если 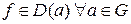 .
.
df.3 Пусть f – дифференцируема в точке  . Дифференциалом функции f в точке
. Дифференциалом функции f в точке 
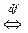 главная линейная относительно приращений аргументов часть полного приращения f в точке
главная линейная относительно приращений аргументов часть полного приращения f в точке  .
.
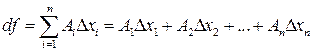
Обозначение 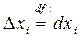 .
.
ЛЕММА.
Если  , где
, где 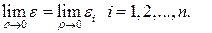
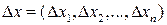 .
.
Доказательство:
Действительно, при  :
:
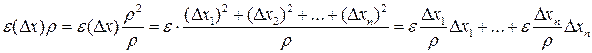 ,
,
Пусть 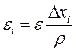 , но
, но 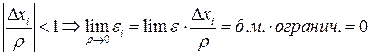
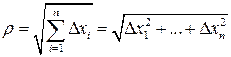 .
.
Th.1 Пусть f дифференцируема в точке  , тогда
, тогда  , или
, или  , тогда
, тогда 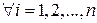
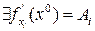 =
=
= 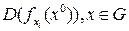 .
.
Доказательство:
Согласно определению №3 и Лемме:  , такая что:
, такая что:
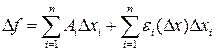 (2)
(2)
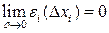
Причем (2) справедливо  , что
, что 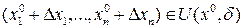 . Пусть
. Пусть 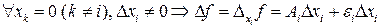 , отсюда при
, отсюда при 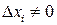 :
:
 - бесконечно малое при
- бесконечно малое при  .
.
По свойству пределов функции одного переменного (Необходимое и достаточное условия существования предела) 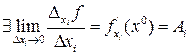 (в обратную сторону неверно).
(в обратную сторону неверно).
СЛЕДСТВИЕ.
Пусть  - дифференцируема в точке
- дифференцируема в точке 
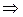 дифференциал f определяется единственным образом формулой:
дифференциал f определяется единственным образом формулой:
Единственность следует из единственности производных.
Th.2 (Необходимое условие дифференцируемости)
Пусть  - дифференцируема в точке
- дифференцируема в точке 
 f –непрерывна в точке
f –непрерывна в точке  или
или 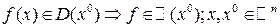 .
.
Доказательство:
Т.к. f – дифференцируема в точке  , то
, то  и
и  ;
;  , т.к.
, т.к. 
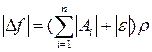 .
.
Предел правой части =0 при 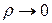
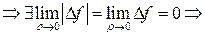 f непрерывна в точке
f непрерывна в точке 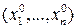 (в обратную сторону утверждение не имеет смысла).
(в обратную сторону утверждение не имеет смысла).
Th.3 (Достаточное условие дифференцируемости)
Пусть  в
в 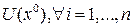 и
и 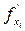 - непрерывна в точке
- непрерывна в точке 
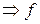 - дифференцируема в точке
- дифференцируема в точке  .
.
Доказательство:
Проведем доказательство для случая 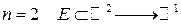 , т.е.
, т.е. 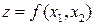 . Найдем приращение:
. Найдем приращение: 
=  (при- меним теорему Лагранжа)=
(при- меним теорему Лагранжа)= 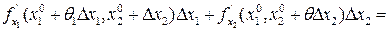
(в силу непрерывности 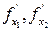 )=
)= 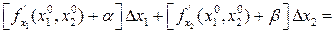
= 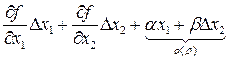 .
.
 или
или 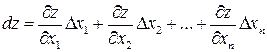 .
.
df.4 Функция, имеющая непрерывные частные производные на множестве G, называется непрерывно-дифференцируемой на G.
Обозначение:  , то будем писать
, то будем писать  .
.
Date: 2015-09-02; view: 363; Нарушение авторских прав