
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Основные понятия. Пространство
|
|
ГЛАВА 7. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ.
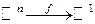
ОСНОВНЫЕ ПОНЯТИЯ. ПРОСТРАНСТВО.
I. (1) Рассмотрим множество действительных чисел 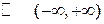 .
.
 ○ ● ●
○ ● ●
0 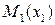

M и x – отождествлены.
Расстояние между точками  равно:
равно:
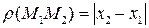 (1)
(1)
Множество вещественных чисел с расстоянием (метрикой) (1) называются пространством 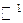 .
.
В терминах расстояния предел последовательности можно перефразировать так:
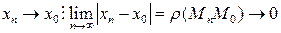 (2)
(2)
т.е. 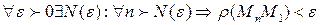 (3)
(3)


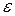
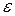
 (●)
(●)

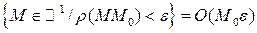
 -
- 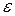 окрестность точки
окрестность точки  .
.
Рассмотрим обобщение пространства 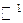 . В тех случаях, когда точки M лежат на плоскости или в пространстве.
. В тех случаях, когда точки M лежат на плоскости или в пространстве.
II. (2) Пространство  .
.
Рассмотрим множество точек плоскости и введем систему координат.

 y
y
● 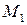
 ●
● 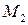
 ○ x
○ x
Пусть  и
и 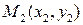 , тогда расстояние между ними:
, тогда расстояние между ними:
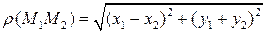 (4)
(4)
Множество точек плоскости с расстоянием (4) называется пространством  .
.
В этом пространстве естественными являются понятия:
df.1 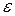 - окрестностью точки
- окрестностью точки  в плоскости называется внутренность круга с центром в точке
в плоскости называется внутренность круга с центром в точке  и радиуса
и радиуса 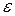 .
.

y

0 x
df.2 Точка  называется внутренней точкой этого множества, если окрестность этой точки содержит только точки, принадлежащие данному множеству (рис.1).
называется внутренней точкой этого множества, если окрестность этой точки содержит только точки, принадлежащие данному множеству (рис.1).
df.3 Если в 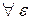 - окрестности точки
- окрестности точки 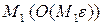 содержатся точки как принадлежащие D, так и не принадлежащие этому множеству, то такая точка называется граничной (рис.1).
содержатся точки как принадлежащие D, так и не принадлежащие этому множеству, то такая точка называется граничной (рис.1).
 y
y
M 
D
0 x
рис.1
ЗАМЕЧАНИЕ.
Совокупность всех граничных точек области D называется ее границей, и обозначают ее 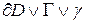 .
.
df.4 Множество D называется открытым, если все его точки являются внутренними относительно D.
Пример.
1) 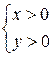 2)
2) 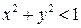
 y
y
x
D
df.5 Множество G называется связным, если две любые точки данного множества можно соединить кривой, все точки которой 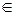 данному множеству.
данному множеству.
Несвязное
Связное G
D
df.6 Множество называется ограниченным, если его можно поместить внутри круга конечного радиуса с центром в начале координат.
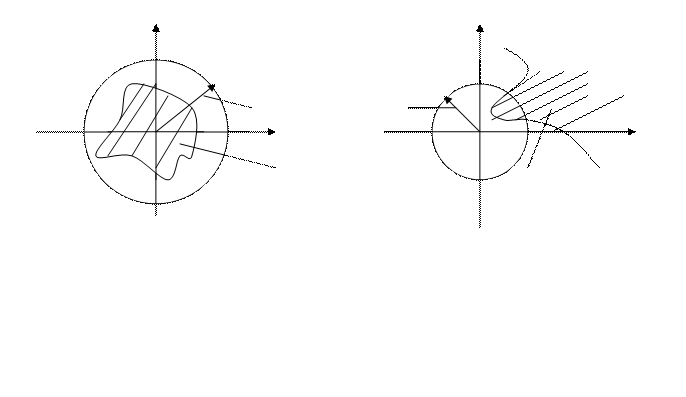 Ограниченное Неограниченное
Ограниченное Неограниченное
R=M R=M
D D 
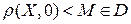
df.7 Областью называется всякое связное открытое множество точек D.
df.8 Всякая область D с присоединенной к ней границей ( ) называется замкнутой областью и обозначается через
) называется замкнутой областью и обозначается через  .
.
III. (3) Пространство  .
.
Все определения пункта II (2) связаны с понятием и свойствами расстояния между точками на плоскости ХОУ; при этом конкретное выражение для расстояния нигде не появлялось.
Основным было понятие окрестности точки.
Будем рассматривать n чисел, которые называются точками:
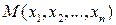 (другими словами n – мерные векторы),
(другими словами n – мерные векторы),  (
( )
)
В этой совокупности введем понятие расстояния (метрики), обобщающее (4).
Пусть 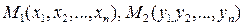 , тогда
, тогда
df.9 Расстояние (метрикой) между точками  называется число:
называется число:
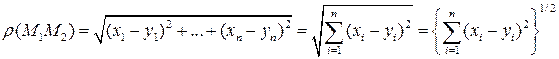 (5)
(5)
df.10 Это множество точек с расстоянием (5) называется пространством  . Пространство
. Пространство  становится метрическим, если ввести метрику одним из равенств:
становится метрическим, если ввести метрику одним из равенств:

ЗАМЕЧАНИЕ.
При n=2 мы получаем пространство  . При n=3 мы получаем трехмерное пространство
. При n=3 мы получаем трехмерное пространство  с обычным (евклидовым) расстоянием.
с обычным (евклидовым) расстоянием.
Все определения предыдущего пункта дословно переносятся на  .
.
Так, например,  - окрестность точки
- окрестность точки  это есть:
это есть:

df.11 n- мерной сферической  -окрестностью данной точки
-окрестностью данной точки 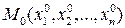 (или открытым шаром радиуса
(или открытым шаром радиуса 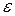 с центром в этой точке) называется множество всех точек
с центром в этой точке) называется множество всех точек 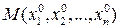 с координатами, удовлетворяющими неравенству:
с координатами, удовлетворяющими неравенству:
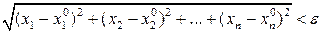 или
или 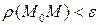 .
.
df.12 Предельной точкой данного множества D точек пространства  называется такая точка
называется такая точка 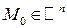 , в любой
, в любой 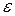 окрестности которой имеется хотя бы одна отличная от
окрестности которой имеется хотя бы одна отличная от  точка M этого множества.
точка M этого множества.
df.13 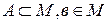 , в – предельная точка A
, в – предельная точка A 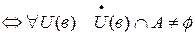 .
.
df.14  (замыкание множества A), если
(замыкание множества A), если  содержит все предельные точки множества A.
содержит все предельные точки множества A.
df.15 A – замкнутое  . Очевидно, что A содержит внутренние (предельные) и граничные точки
. Очевидно, что A содержит внутренние (предельные) и граничные точки 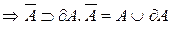 .
.
Date: 2015-09-02; view: 349; Нарушение авторских прав