
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

П. 8 Классы интегрируемых функций
|
|
Теорема 1.  .
.
Доказательство:
Пусть функция  непрерывна на отрезке
непрерывна на отрезке 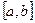 , Тогда по теореме Кантора она равномерно непрерывна на этом отрезке. Зафиксируем некоторое
, Тогда по теореме Кантора она равномерно непрерывна на этом отрезке. Зафиксируем некоторое  . Тогда для
. Тогда для 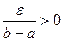 найдется такое
найдется такое 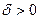 , что для разбиения отрезка
, что для разбиения отрезка 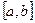 на отрезки
на отрезки 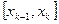 , длины которых
, длины которых  , все колебания функции
, все колебания функции  на отрезках разбиения удовлетворяют условию
на отрезках разбиения удовлетворяют условию  . Отсюда получим
. Отсюда получим  при условии
при условии 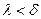 . Следовательно, для непрерывной функции
. Следовательно, для непрерывной функции  на отрезке
на отрезке 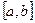 выполнено достаточное условие интегрируемости. Значит, существует определенный интеграл
выполнено достаточное условие интегрируемости. Значит, существует определенный интеграл 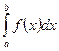 . ■
. ■
Теорема 2. Если функция  ограничена и непрерывна на отрезке
ограничена и непрерывна на отрезке 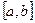 , кроме конечного числа точек разрыва, то функция
, кроме конечного числа точек разрыва, то функция  интегрируема на отрезке
интегрируема на отрезке 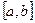 .
.
Доказательство:
Достаточно рассмотреть случай одной точки 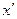 разрыва на отрезке
разрыва на отрезке 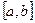 . Пусть
. Пусть 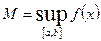 ,
,  ,
, 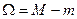 - колебание функции
- колебание функции  на отрезке
на отрезке 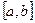 . Возьмем любое достаточно малое
. Возьмем любое достаточно малое  и рассмотрим отрезки
и рассмотрим отрезки  и
и 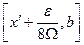 . На каждом из этих отрезков функция
. На каждом из этих отрезков функция  непрерывна. Следовательно, найдется такое
непрерывна. Следовательно, найдется такое 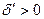 , что при разбиении их на частичные отрезки
, что при разбиении их на частичные отрезки  , длины которых
, длины которых 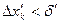 , все колебания функции
, все колебания функции  на этих отрезках разбиения удовлетворяют условию
на этих отрезках разбиения удовлетворяют условию 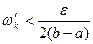 . Пусть
. Пусть  . Рассмотрим произвольное разбиение отрезка
. Рассмотрим произвольное разбиение отрезка 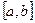 на частичные отрезки
на частичные отрезки 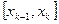 , длины которых
, длины которых  . Для этого разбиения рассмотрим
. Для этого разбиения рассмотрим  , где первая сумма составляется по частичным отрезкам, целиком лежащих вне
, где первая сумма составляется по частичным отрезкам, целиком лежащих вне 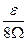 -окрестности точки
-окрестности точки 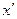 , а вторая сумма – по отрезкам, либо целиком лежащих в этой окрестности, либо имеющих общие с ней точки. Тогда имеем
, а вторая сумма – по отрезкам, либо целиком лежащих в этой окрестности, либо имеющих общие с ней точки. Тогда имеем 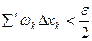 .
.
Длины отрезков, целиком попавших в 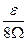 -окрестность точки
-окрестность точки 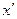 , в сумме не превосходит
, в сумме не превосходит 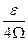 . Число отрезков, лишь частично попавших в эту окрестность, не больше двух, поэтому сумма их длин меньше
. Число отрезков, лишь частично попавших в эту окрестность, не больше двух, поэтому сумма их длин меньше  . Следовательно,
. Следовательно, 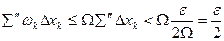 . Таким образом,
. Таким образом,  при условии
при условии 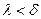 . ■
. ■
Теорема 3. Если функция  монотонна на отрезке
монотонна на отрезке 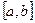 , то она интегрируема на отрезке
, то она интегрируема на отрезке 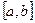 .
.
Доказательство:
Пусть для определенности функция  монотонно возрастает на отрезке
монотонно возрастает на отрезке 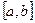 . Если
. Если 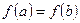 , то
, то 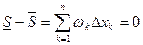 независимо от разбиения отрезка
независимо от разбиения отрезка 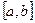 . Если
. Если 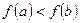 , то для некоторого
, то для некоторого  возьмем
возьмем 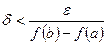 . Пусть
. Пусть  - произвольное разбиение, для которого
- произвольное разбиение, для которого 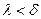 . Тогда
. Тогда 
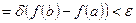 . ■
. ■
Date: 2015-09-02; view: 753; Нарушение авторских прав