Задачи и упражнения для самостоятельной работы

1. Даны матрицы 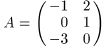и .

Найдите: а) 3 A + 2 B; 6) A − 4 B; в) числа x и y такие, что все элементы матрицы xA + yB равны нулю.

2. Докажите свойства 1°−5° линейных операций над матрицами.

3. Даны матрицы 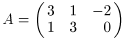и .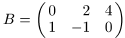

Найдите: а) A^Т; б) 2 A^Т + B^Т; в) 3 A^Т − 2 B^Т.

4. Докажите справедливость равенств:

а) (хА) ^Т = xA^Т (x − число); б) (A + В) ^Т = A^Т + B^Т; в) (A^Т) ^Т = A.

5. Найдите AB, BA, A^ТB^Т и B^ТA^Т, если:

а)

б)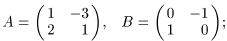

в) А = (d_ija_ij) _{n × n}, B = (d_ijb_ij) _{n × n}, d_ij − символ Кронекера;

г)

д)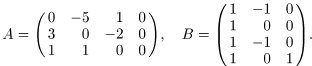

6. Докажите свойства 1°−3° умножения матриц.

7. Докажите, что для любой m × n -матрицы A справедливо равенство:

а) AE_n = A, где E_n − единичная матрица n -го порядка;

б) E_mA = A, где E_m − единичная матрица m -го порядка.

8. Найдите матрицу X из уравнения:

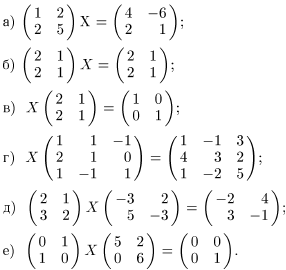
9. Найдите обратную матрицу для матрицы:

а) 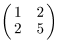; б) ;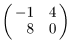

в) 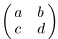при условии ad − bc ≠ 0;

г) 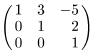; д) ;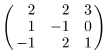

е) (a_ijd_ij) _{n × n}, где d_ij − символ Кронекера, a_ij ≠ 0 при i = 1,..., n.

10. Дана матрица 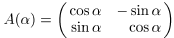. Докажите, что:

а) А (a) А (b) = А (a + b); б) А ⁻¹(a) = А (− a); в) А ⁻¹(a) = А^T (a).

11. Дана матрица 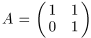. Докажите, что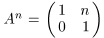
при n = ±1, ±2,..., где А ^{− n} = (А ⁻¹) ⁿ.