Глава I. Матрицы и определители. § 1

ГЛАВА I. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ. § 1

Матрицы

Основные понятия

1. Понятие матрицы. Прямоугольная таблица чисел (вещественных или комплексных)

называется числовой матрицей (или просто матрицей). Числа a_ij называются элементами матрицы; первый индекс i обозначает номер строки, а второй индекс j − номер столбца, на пересечении которых стоит элемент a_ij. Например, элемент a ₁₂ стоит на пересечении первой строки и второго столбца.

Матрица A имеет m строк и n столбцов. Поэтому ее называют m × n -матрицей или матрицей с размерами m × n.

Для m × n -матрицы А можно использовать краткое обозначение (a_ij) _{m × n} , а если размеры матрицы заранее оговорены, то, не указывая их, будем писать (a_ij).

Если m = n (число строк матрицы равно числу столбцов), то матрица называется квадратной матрицей n -го порядка.

Две m × n -матрицы А = (a_ij) и B = (b_ij) называются равными (А = В), если их элементы соответственно равны: a_ij = b_ij, i = 1,..., m; j = l,..., n.

2. Линейные операции над матрицами. Суммой (разностью) m × n -матриц А = (a_ij) и B = (b_ij) называется m × n -матрица C = (c_ij), элементы которой равны суммам (разностям) соответствующих элементов матриц А и B: c_ij = a_ij + b_ij (c_ij = a_ij − b_ij).

Обозначение: C = A + B (C = A − B).

Подчеркнем, что сложение и вычитание вводятся для матриц только с одинаковыми размерами.

Произведением m × n -матрицы А = (a_ij) на число х называется m × n -матрица B = (b_ij), элементы которой равны произведениям соответствующих элементов матрицы A на число х: b_ij = xa_ij.

Обозначение: В = xA.

Введенные действия (сложение и вычитание матриц, умножение матрицы на число) называются линейными операциями над матрицами. Они обладают следующими свойствами. Для любых m × n -матриц A, B, C и любых чисел x и y справедливы равенства 1°−5°.

1°. A + B = B + A (коммутативность сложения).

2°. (A + B) + C = A + (B + C) (ассоциативность сложения).

3°. х (A + B) = xA + xB (распределительное свойство относитель- но числового сомножителя).

4°. (x + y) A = xA + yA (распределительное свойство относительно матричного сомножителя).

5°. x (yA) = (xy) A.

3. Транспонированная матрица. Расположим строки m × n - матрицы A = (a_ij) в виде столбцов, не меняя их порядка (т. е. первая строка станет первым столбцом и т.д.). Получится n × m -матрица

,

которая называется транспонированной по отношению к матрице A и обозначается A^Т.

Обозначим элементы матрицы A^Т через a_ij^Т (i = 1,..., n; j = 1,..., m). Согласно определению транспонированной матрицы справедливы равенства

Операция транспонирования (т. е. переход от матрицы A к матрице A^Т) обладает следующими свойствами. Для любых m × n -матриц A и B и любого числа х справедливы равенства 1°, 2°.

1°. (A + B) ^Т = A^Т + B^Т.

2°. (xA) ^Т = xA^Т.

4. Умножение матриц. Произведением матрицы А = (a_ij) _{m × n} на матрицу B = (b_ij) _{n × k} называется матрица C = (c_ij) _{m × k} , элементы которой определяются формулой

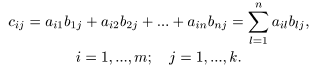
Обозначение: C = AB.

Подчеркнем, что произведение AB определено только для таких матриц, у которых число столбцов матрицы A (первого сомножителя) равно числу строк матрицы B (второго сомножителя). При этом число строк матрицы С = AВ равно числу строк матрицы A, а число столбцов матрицы С равно числу столбцов матрицы В.

Умножение матриц обладает следующими свойствами. Для любых матриц A, В, С и любого числа х справедливы равенства 1°−4° (предполагается, что размеры матриц A, В, С таковы, что левые части равенств определены, тогда будут определены и правые части равенств).

1°. A (ВС) = (AВ) С (ассоциативность умножения).

2°. A (В + С) = AВ + AС (распределительное свойство).

3°. (хA) В = A (xВ) = x (AВ).

4°. (AВ) ^Т = В^ТA^Т.

Отметим, что умножение матриц не обладает свойством коммутативности. Более того, если A − m × n -матрица, а В − n × k -матрица, то произведение AВ определено, а произведение ВA при k ≠ m не определено. Если же k = m, то произведение ВA также определено, но при m ≠ n AВ и ВA − квадратные матрицы разных порядков (соответственно порядка тип), так что вопрос об их равенстве некорректен. Если же m = n = k, то обе матрицы AВ и ВA − квадратные матрицы n -го порядка, но и в этом случае, вообще говоря, AВ ≠ ВA.

5. Обратная матрица. Введем так называемый символ Кронекера:

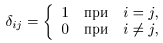
где i и j − произвольные натуральные числа.

Матрица

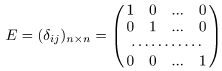
называется единичной матрицей n -го порядка. Для нее используются также следующие обозначения: Е_n, I, I_n.

Квадратная матрица B называется обратной по отношению к матрице A с такими же размерами, если

AB = BA = E.

Обратная матрица обозначается символом А ⁻¹.

ГЛАВА I. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ. § 1