Примеры решения задач. а) По определению суммы матриц

1. Даны матрицы 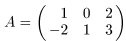и .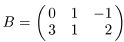

Найти: а) А + В; б) 2В; в) В^T; г) AВ^T; д) В^TA.

Решение.

а) По определению суммы матриц

.

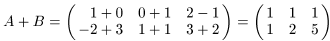б) По определению произведения матрицы на число

.

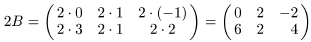в) По определению транспонированной матрицы

.

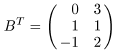г) По определению произведения матриц

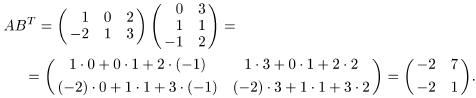
д) Аналогично пункту г) находим

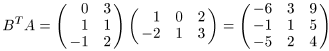.n

2. Дана система m линейных уравнений с n неизвестными

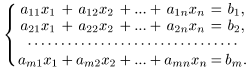
Здесь:

a_ij, b_i (i = 1, ... , m; j = 1, ... , n) − известные числа;

x_i (i = 1, ... , n) − неизвестные.

Записать эту систему в матричном виде.

Решение.

Введем m × n-матрицу А с элементами a_ij и столбцы В с элементами b₁,..., b_m и X с элементами x₁,..., x_n. Тогда данную систему можно записать в виде АХ = В.n

3. Доказать равенство (АB)^Т = А^ТB^Т.

Решение.

Пусть А = (a_ij)_{m × n}, B = (b_ij)_{n × k} − Согласно определению произведения матриц элементы c_ij матрицы C = AВ вычисляются по формуле

.

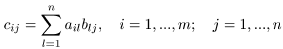(2)

Элементы матриц А^Т, B^Т, C^Т и D = B^ТA^Т обозначим соответственно через a_ij^Т, b_ij^Т, c_ij^Т и d_ij. Тогда в соответствии с равенством (1) имеем

а элементы d_ij матрицы D = B^ТA^Т вычисляются по формуле

.

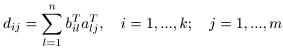Отсюда, учитывая равенства (2) и (3), получаем

.

Таким образом, элементы матриц D и C^Т соответственно равны, поэтому C^Т = D, т. е. (AB)^Т = B^ТA^Т, что и требовалось доказать.

4. Для матрицы найти обратную.

Решение.

Положим

.

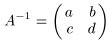По определению обратной матрицы A⁻¹A = Е, т. е.

.

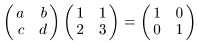Перемножая матрицы в левой части равенства и приравнивая элементы полученной матрицы соответствующим элементам матрицы в правой части равенства, приходим к системе уравнений

а + 2b = 1, а + 3b = 0, c + 4d = 0, c + 3d = l,

откуда находим а = 3, b = −1, c = −2, d = 1. Итак, матрица

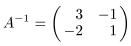
удовлетворяет условию A⁻¹A = Е.

Нетрудно проверить, что равенство AA⁻¹ = Е также выполняется.

Таким образом, найденная матрица A⁻¹ обратная по отношению к матрице А.

Date: 2015-09-02; view: 107; Нарушение авторских прав