Задачи на работу

Задачи на работу схожи с задачами на движение. Для их решения используется такая же математическая модель, что и при решении задач на движение. Речь идет о ключевой формуле:

V = p*t, где

V – объем работы;

p – производительность труда, скорость работы (объем работы, выполненной за единицу времени);

t – время работы.

Если в задаче объем в явном виде не задан, то его можно принять равным единице.

Задачи на совместную работу решаются с помощью такой же математической модели, что и задачи на движение навстречу: роль скорости сближения здесь играет общая производительность.

Ключевая задача: «Первый мастер может выполнить некоторую работу за х часов, а второй может выполнить эту же работу за у часов. За какое время они выполнят эту работу, работая вместе?»

Так как объем работы не задан, то можно принять его равным единице. Тогда:

- производительность первого мастера, то есть такую часть работы он выполняет за 1 час;

- производительность второго мастера;

- общая производительность мастеров, то есть такую часть работы они выполняют за 1 час, работая вместе;

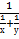- время, за которое они выполнят эту работу, работая вместе.

Также в задачах на работу выделяют группу задач на трубы и бассейны, решение которых не имеет никаких отличий от решения других задач на работу.

Задача 1: «Один мастер может выполнить заказ за 12 часов, а другой — за 6 часов. За сколько часов выполнят заказ оба мастера, работая вместе?»

Объем работы принимаем равным единице.

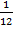- производительность первого мастера;

- производительность второго мастера;

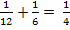- общая производительность;

1: = 4 (ч) – время, за которое мастера выполнят работу, работая вместе.

Ответ: 4 ч.

Задача 2: «Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно?»

Объем работы принимаем равным единице. 1 ч = 60 мин.

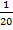- производительность первого насоса;

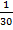- производительность второго насоса;

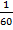– производительность третьего насоса;

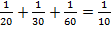- общая производительность;

1: 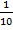= 10 (мин) – время, за которое насосы наполнят бак, работая одновременно.

Ответ: 10 мин.

Задача 3: «Игорь и Паша красят забор за 9 часов. Паша и Володя красят этот же забор за 12 часов, а Володя и Игорь – за 18 часов. За сколько часов мальчики покрасят забор, работая втроем?»

Объем работы – единица.

- производительность Игоря и Паши при одновременной работе;

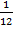- производительность Паши и Володи при одновременной работе;

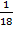- производительность Володи и Игоря при одновременной работе;

- удвоенная производительность Игоря, паши и Володи при одновременной работе;

: 2 = - производительность Игоря, паши и Володи при одновременной работе;

1: = 8 (ч) – время, за которое мальчики покрасят забор, работая втроем.

Ответ: 8 ч.

Задача 4: «Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?»

	Объем работы, колич.дет.	Производительность, дет. в час	Время, ч
Первый рабочий		х + 1		На 1 ч меньше
Второй рабочий		х

Уравнение:
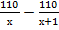= 1

Ответ: 10 дет.

Задача 5: «Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй – за три дня?»

Объем работы – единица.

	Общая производительность	Производительность	Время, дн.	Объем работы
Первый		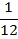х		2х	=
Второй		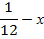	3()

Уравнение: 2х = 3().

х = 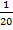- производительность первого рабочего;

20 дней – время работы первого рабочего в одиночку.

Ответ: 20 дней.

Задача 6: «Даша и Маша про­па­лы­ва­ют гряд­ку за 12 минут, а одна Маша — за 20 минут. За сколь­ко минут про­па­лы­ва­ет гряд­ку одна Даша?»

Объем работы – единица.

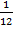- общая производительность;

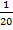- производительность Маши;

- производительность Даши;

30 мин – время, которое потребуется Даше на прополку.

Ответ: 30 мин.

Тренировочные задачи:

1. Заказ на 156 де­та­лей пер­вый ра­бо­чий вы­пол­ня­ет на 1 час быст­рее, чем вто­рой. Сколь­ко де­та­лей в час де­ла­ет пер­вый ра­бо­чий, если из­вест­но, что он за час де­ла­ет на 1 де­таль боль­ше? (13)

2. На из­го­тов­ле­ние 475 де­та­лей пер­вый ра­бо­чий тра­тит на 6 часов мень­ше, чем второй ра­бо­чий на из­го­тов­ле­ние 550 таких же де­та­лей. Из­вест­но, что пер­вый рабочий за час де­ла­ет на 3 де­та­ли боль­ше, чем вто­рой. Сколь­ко де­та­лей в час делает пер­вый ра­бо­чий? (25)

3. На из­го­тов­ле­ние 99 де­та­лей пер­вый ра­бо­чий тра­тит на 2 часа мень­ше, чем вто­рой ра­бо­чий на из­го­тов­ле­ние 110 таких же де­та­лей. Из­вест­но, что пер­вый ра­бо­чий за час де­ла­ет на 1 де­таль боль­ше, чем вто­рой. Сколь­ко де­та­лей в час де­ла­ет вто­рой рабо­чий? (10)

4. Пер­вая труба про­пус­ка­ет на 1 литр воды в ми­ну­ту мень­ше, чем вто­рая. Сколь­ко лит­ров воды в ми­ну­ту про­пус­ка­ет пер­вая труба, если ре­зер­ву­ар объ­е­мом 110 литров она за­пол­ня­ет на 1 ми­ну­ту доль­ше, чем вто­рая труба? (10)

5. Пер­вая труба про­пус­ка­ет на 1 литр воды в ми­ну­ту мень­ше, чем вто­рая. Сколь­ко лит­ров воды в ми­ну­ту про­пус­ка­ет вто­рая труба, если ре­зер­ву­ар объ­е­мом 110 литров она за­пол­ня­ет на 1 ми­ну­ту быст­рее, чем пер­вая труба? (11)

6. Пер­вая труба про­пус­ка­ет на 1 литр воды в ми­ну­ту мень­ше, чем вто­рая. Сколь­ко лит­ров воды в ми­ну­ту про­пус­ка­ет пер­вая труба, если ре­зер­ву­ар объ­е­мом 110 литров она за­пол­ня­ет на 2 ми­ну­ты доль­ше, чем вто­рая труба за­пол­ня­ет резерву­ар объ­е­мом 99 лит­ров? (10)

7. Пер­вая труба про­пус­ка­ет на 5 лит­ров воды в ми­ну­ту мень­ше, чем вто­рая. Сколь­ко лит­ров воды в ми­ну­ту про­пус­ка­ет вто­рая труба, если ре­зер­ву­ар объ­е­мом 375 литров она за­пол­ня­ет на 10 минут быст­рее, чем пер­вая труба за­пол­ня­ет ре­зер­ву­ар объ­е­мом 500 лит­ров? (25)

8. Каж­дый из двух ра­бо­чих оди­на­ко­вой ква­ли­фи­ка­ции может вы­пол­нить заказ за 15 часов. Через 3 часа после того, как один из них при­сту­пил к вы­пол­не­нию за­ка­за, к нему при­со­еди­нил­ся вто­рой ра­бо­чий, и ра­бо­ту над за­ка­зом они до­ве­ли до конца уже вме­сте. Сколь­ко часов по­тре­бо­ва­лось на вы­пол­не­ние всего за­ка­за? (9)

9. Две трубы на­пол­ня­ют бас­сейн за 3 часа 36 минут, а одна пер­вая труба на­пол­ня­ет бас­сейн за 6 часов. За сколь­ко часов на­пол­ня­ет бас­сейн одна вто­рая труба? (9)

10. Пер­вая труба на­пол­ня­ет ре­зер­ву­ар на 6 минут доль­ше, чем вто­рая. Обе трубы напол­ня­ют этот же ре­зер­ву­ар за 4 ми­ну­ты. За сколь­ко минут на­пол­ня­ет этот резерву­ар одна вто­рая труба? (6)

11. В по­мощь са­до­во­му на­со­су, пе­ре­ка­чи­ва­ю­ще­му 5 лит­ров воды за 2 ми­ну­ты, подключи­ли вто­рой насос, пе­ре­ка­чи­ва­ю­щий тот же объем воды за 3 ми­ну­ты. Сколь­ко минут эти два на­со­са долж­ны ра­бо­тать сов­мест­но, чтобы пе­ре­ка­чать 25 лит­ров воды? (6)

12. Петя и Ваня вы­пол­ня­ют оди­на­ко­вый тест. Петя от­ве­ча­ет за час на 8 во­про­сов текста, а Ваня – на 9. Они од­но­вре­мен­но на­ча­ли от­ве­чать на во­про­сы теста, и Петя за­кон­чил свой тест позже Вани на 20 минут. Сколь­ко во­про­сов со­дер­жит тест? (24)

13. Пли­точ­ник дол­жен уло­жить 175 м² плит­ки. Если он будет укла­ды­вать на 10 м² в день боль­ше, чем дол­жен, то за­кон­чит ра­бо­ту на 2 дня рань­ше. Сколь­ко квадратных мет­ров плит­ки в день дол­жен укла­ды­вать пли­точ­ник? (25)

14. Пер­вый и вто­рой на­со­сы на­пол­ня­ют бас­сейн за 10 минут, вто­рой и тре­тий — за 15 минут, а пер­вый и тре­тий — за 24 ми­ну­ты. За сколь­ко минут три эти на­со­са заполнят бас­сейн, ра­бо­тая вме­сте? (9,6)

15. Пер­вый и вто­рой на­со­сы на­пол­ня­ют бас­сейн за 9 минут, вто­рой и тре­тий — за 12 минут, а пер­вый и тре­тий — за 18 минут. За сколь­ко минут эти три на­со­са за­пол­нят бас­сейн, ра­бо­тая вме­сте? (8)

16. Пер­вый и вто­рой на­со­сы на­пол­ня­ют бас­сейн за 10 минут, вто­рой и тре­тий — за 15 минут, а пер­вый и тре­тий — за 18 минут. За сколь­ко минут эти три на­со­са за­пол­нят бас­сейн, ра­бо­тая вме­сте? (9)

Date: 2015-09-02; view: 720; Нарушение авторских прав