
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

I.Задачи на движение по прямой
|
|
Задачи на движение
Для успешного решения задач на движение нужно твердо знать ключевую формулу – формулу движения, в которой связаны путь, скорость и время движения:
S=vt, где
S – это пройденный путь или расстояние;
v – это скорость движения, то есть расстояние, пройденное за единицу времени;
t – время движения.
Зная эту формулу, можно легко вывести из нее формулу для скорости или времени: v=S/t; t=S/v.
Практические советы для успешного решения:
1. Вспоминаем ключевую формулу S=vt. Для наглядности можно ее записать.
2. Определяемся, какую величину обозначим за икс, расписываем через икс все данные. Особое внимание обращаем на величины, входящие в формулу-ключ: скорость, время, расстояние. Эти величины – основа решения задач на движение. Зачастую бывает удобно всю информацию разместить в таблице.
3. До составления уравнения, приводим (если надо) все величины задачи к единым единицам измерения.
4. Записываем уравнение.
5. Решаем уравнение. При получении двух корней, за ответ берем корень, подходящий по условию задачи.
Типы задач на движение:
I. Задачи на движение по прямой.
II. Задачи на движение по окружности.
III. Задачи на движение по воде.
I.Задачи на движение по прямой
Типы задач на движение по прямой:
1. Задачи на движение одного объекта.
2. Задачи на движение двух объектов.
3. Задачи на встречное движение и движение в противоположных направлениях.
4. Задачи на движение в одном направлении.
5. Задачи на среднюю скорость движения.
6. Задачи на движение протяженных объектов, например, поездов.
· Задачи на движение одного объекта.
Используя формулы, найдите неизвестные величины в таблице:
| Расстояние | 124 км | 595 км | |
| Время | 62 км/ч | 28 км/ч | |
| Скорость | 7 ч | 3 ч |
Покажем теперь на примере, как составить уравнение задачи на движение.
Задача 1: «Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 70 км. На следующий день он отправился обратно в A со скоростью на 3 км/ч больше прежней. По дороге он сделал остановку на 3 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из B в A. Ответ дайте в км/ч.»
Как составить таблицу по условию задачи? Вот один из приемов.
В первый столбец таблицы нужно записать ту величину, которая по условию задачи известна. В нашем примере – это расстояние. Во второй столбец нужно записать ту величину, которую нужно найти. Эту величину удобно брать за икс, тогда решив уравнение, мы сразу ответим на вопрос задачи. В нашем примере неизвестная величина – это скорость. В третий столбец запишем ту величину, которая осталась. В нашем примере – это время.
| Расстояние, км | Скорость, км/ч | Время, ч | ||
| Из А в В | х – 3 | 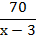
| = | |
| Из В в А | х | 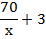
|
Теперь нужно найти в условии задачи предложение, которое свяжет время, затраченное на путь из А в В, и время, затраченное на путь из В в А. Вот оно: «В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из A в B». Теперь можно составить уравнение:
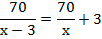
Решаем уравнение и получаем ответ: 10 км/ч.
Рассмотрим еще один пример.
Задача 2: «Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Пешеход прошёл путь из А в В за 2 часа 45 минут. Время его движения на спуске составило 1 час 15 минут. С какой скоростью пешеход шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 2 км/ч? Ответ выразите в км/ч».
Приведем величины задачи к единым единицам измерения:
2 ч 45 мин = 2  ч =
ч = 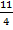 ч; 1 ч 15 мин = 1
ч; 1 ч 15 мин = 1  ч =
ч =  ч.
ч.
Теперь составим таблицу.
| Время, ч | Скорость, км/ч | Расстояние, км | ||
| Подъем | 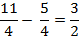
| х – 2 |  (х – 2) (х – 2)
| 8 км |
| Спуск | 
| х |  х х
|
Уравнение:  (х – 2) +
(х – 2) +  х = 8.
х = 8.
Ответ: 4 км/ч.
Тренировочные задачи.
1. Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из A в B. Ответ дайте в км/ч. (7)
2. Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Турист прошёл путь из А в В за 5 часов. Время его движения на спуске составило 1 час. С какой скоростью турист шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 3 км/ч? (4)
3. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 128 км. На следующий день он отправился обратно в А со скоростью на 8 км/ч больше прежней. По дороге он сделал остановку на 8 часов. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из В в А. Ответ дайте в км/ч. (16)
· Задачи на движение двух объектов
Задача 1: «Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути – со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч».
Если расстояние явно не задано, можно ввести вспомогательную переменную, которая после составления уравнения сократится.
| Расстояние, км | Скорость, км/ч | Время, ч | |||
| Первый автомобиль | S | x | 
| = | |
| Второй автомобиль | S | x+16 | 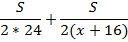
| ||
Составляем уравнение:
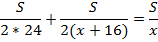
Разделим обе части уравнения на S  :
:

Ответ: 32 км/ч.
Задача 2: «Из пункта A в пункт B, расстояние между которыми 75 км, одновременно выехали автомобилист и велосипедист. Известно, что за час автомобилист проезжает на 40 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 6 часов позже автомобилиста. Ответ дайте в км/ч.»
| Расстояние, км | Скорость, км/ч | Время, ч | ||
| Велосипедист | х | 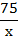
| На 6 ч > | |
| Автомобилист | х+40 | 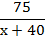
|
Составляем уравнение:
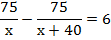
Ответ: 10 км/ч.
Тренировочные задачи:
1. Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути – со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч. (52)
2. Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч. (16)
3. Два велосипедиста одновременно отправились в 88–километровый пробег. Первый ехал со скоростью, на 3 км/ч большей, чем скорость второго, и прибыл к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч. (8)
4. Товарный поезд каждую минуту проезжает на 750 метров меньше, чем скорый, и на путь в 180 км тратит времени на 2 часа больше, чем скорый. Найдите скорость товарного поезда. Ответ дайте в км/ч. (45)
5. Иван и Алексей договорились встретиться в N-ске. Иван звонит Алексею и узнаёт, что тот находится в 275 км от N-ска и едет с постоянной скоростью 75 км/ч. Иван в момент разговора находится в 255 км от N-ска и ещё должен по дороге сделать 50-минутную остановку. С какой скоростью должен ехать Иван, чтобы прибыть в N-ск одновременно с Алексеем? (90)
· Задачи на встречное движение и движение в противоположных направлениях.
При решении задач на встречное движение полезно использовать понятие «скорость сближения», которая находится сложением скоростей движущихся объектов. Как связаны между собой расстояние, скорость и время при движении тел навстречу друг другу?
S = (v1 + v2) t, где
S – расстояние между объектами до начала движения;
v1 + v2 – скорость сближения объектов;
t – время до встречи.
Задача 1: «Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?»
1) 65 + 75 = 140 (км/ч) – скорость сближения
2) 560/140 = 4 (ч) – время, через которое встретятся автомобили
Ответ: 4 ч.
Задача 2: «Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?»
Приведем величины задачи к единым единицам измерения:
48 мин =  ч.
ч.
Если расстояние явно не задано, можно принять его равным единице. Составим таблицу:
| Расстояние | Время, ч | Скорость | Скорость сближения | Время до встречи, ч | Расстояние | ||
| Вел. | х | 
| 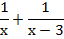
| 
| (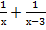 ) ) 
| =1 | |
| Мот. | х – 3 | 
|
Составляем уравнение:
(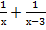 )
)  = 1
= 1
Ответ: 4 ч.
Тренировочные задачи:
1. Из городов А и В, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города В. Найдите скорость автомобиля, выехавшего из города А. Ответ дайте в км/ч. (50)
2. Расстояние между городами А и В равно 435 км. Из города А в город В со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города В выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города А автомобили встретятся? Ответ дайте в километрах. (240)
3. Расстояние между городами А и В равно 470 км. Из города А в город В выехал первый автомобиль, а через 3 часа после этого навстречу ему из города В выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города А. Ответ дайте в км/ч. (70)
4. Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 4,4 км от места отправления. Один идёт со скоростью 2,5 км/ч, а другой — со скоростью 3 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча? (4)
5. Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 4 часа раньше, чем велосипедист приехал в A, а встретились они через 50 минут после выезда. Сколько часов затратил на путь из B в A велосипедист? (5)
При решении задач на движение в противоположных направлениях полезно использовать понятие «скорость удаления», которая находится сложением скоростей движущихся объектов. Как связаны между собой расстояние, скорость и время при движении тел в противоположных направлениях? Такой же точно формулой, что и при движении навстречу:
S = (v1 + v2) t, где
S – расстояние между объектами после их удаления друг от друга;
v1 + v2 – скорость удаления объектов;
t – время движения.
Задача: «Из деревни Простоквашино одновременно оправились на поиски пропавшей коровы Мурки кот Матроскин и пес Шарик. Один из них побежал в южном направлении, другой – в северном. Через полчаса расстояние между ними стало равным 16 км, причем Шарик пробежал на 6 км больше, чем Матроскин. С какой скоростью бежал каждый из них?»
1) 16:  = 32 (км/ч) – скорость удаления;
= 32 (км/ч) – скорость удаления;
2) 16 – 6 = 10 (км) – удвоенное расстояние, которое пробежал Матроскин;
3) 10 / 2 = 5 (км) – расстояние, которое пробежал Матроскин за 30 мин;
4) 5*2 = 10 (км/ч) – скорость Матроскина;
5) 32 – 10 = 22 (км/ч) – скорость Шарика.
Ответ: 10 км/ч; 22 км/ч.
Тренировочные задачи:
1. Из одного пункта в противоположных направлениях вышли два пешехода. Скорость одного из них 6 км/час, и он был в пути на 2 час больше, чем другой. Скорость другого составляла 2/3 скорости первого. Сколько времени был в пути каждый пешеход, если они удалились друг от друга на 28км?
2. Папа и сын плывут на лодке против течения. В какой-то момент сын уронил за борт папину шляпу. Только через 15 мин. Папа заметил пропажу, быстро развернул лодку, и они поплыли по течению с той же собственной скоростью. За сколько минут они догонят шляпу? (15)
· Задачи на движение в одном направлении.
В задачах на движение в одном направлении при одновременном начале движения объектов полезно использовать понятия «скорость сближения» и «скорость удаления», которые находятся вычитанием меньшей скорости из большей. Расстояние, скорость и время при движении тел с отставанием и движении тел вдогонку связаны одной и той же формулой: S = (v1 – v2) t, где
v1 > v2;
S – расстояние между телами в конце движения при движении с отставанием и расстояние между телами до начала движения при движении вдогонку;
(v1 – v2) – скорость удаления при движении тел с отставанием и скорость сближения при движении тел вдогонку;
t – время движения при движении с отставанием и время до встречи при движении вдогонку.
Задача 1: «Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 1,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 300 метрам?»
1) 300 м = 0,3 км;
2) Так как скорость первого пешехода на 1,5 км/ч больше скорости второго, то 1,5 км/ч – это и есть скорость удаления пешеходов.
3) 0,3 / 1,5 =  (ч) – время движения;
(ч) – время движения;
4)  ч = 12 мин.
ч = 12 мин.
Ответ: 12 мин.
Задача 2: «Расстояние между городами А и В равно 150 км. Из города А в город В выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль прибыл в В. Найдите расстояние от А до С. Ответ дайте в километрах»
Эта задача комбинированная: на движение вдогонку и на движение в противоположных направлениях. 30 мин =  ч
ч
| Время, ч | Скорость, км/ч | Расст., км | Скор. сближ., км/ч | Время встречи, ч | Время движ. в против. напр., ч | Скор. удал., км/ч | Расстояние между А и В, км | ||
| А. | 
| х | 
| 90 – х | 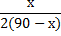
| 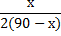
| 90+х | 
| 150 км |
| М. |
Уравнение:
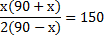
х = 60 (км/ч) – скорость автомобилиста.
Иногда вопрос задачи неудобно брать за икс. Часто в задачах на движение бывает удобно брать за икс скорость.Тогда в задаче появляются дополнительные действия, которые надо потом не забыть сделать:
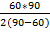 = 90 (км) – расстояние от А до С.
= 90 (км) – расстояние от А до С.
Ответ: 90 км.
Можно решить эту задачу другим способом, составив систему уравнений.
Пусть v км/ч – скорость движения автомобиля, t ч – время движения мотоциклиста из А в С. Тогда (t +  ) v = 90t и (2t +
) v = 90t и (2t +  ) v = 150. Решим систему полученных уравнений:
) v = 150. Решим систему полученных уравнений:

90*1 = 90 (км) – расстояние от А до С.
Ответ: 90 км.
Тренировочные задачи:
1. Расстояние между городами A и B равно 198 км. Из города A в город B выехал автомобиль, а через 3 часа следом за ним со скоростью 80 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в B. Найдите расстояние от A до C. Ответ дайте в километрах.
2. Два пешехода отправляются одновременно в одном направлении из одного и того же места на прогулку по аллее парка. Скорость первого на 0,5 км/ч больше скорости второго. Через сколько минут расстояние между пешеходами станет равным 25 метрам? (3)
3. Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого. Ответ дайте в км/ч. (25)
· Задачи на среднюю скорость движения.
Напомним, что средняя скорость вычисляется по формуле: v =  , где
, где
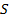 - путь, пройденный телом;
- путь, пройденный телом;
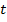 - время, за которое этот путь пройден.
- время, за которое этот путь пройден.
Если путь состоит из нескольких участков, то следует вычислить всю длину пути и все время движения. Например, если путь состоял из двух участков протяженностью s1 и s2, скорости на которых были равны соответственно v1 и v2, то
S = s1 + s2, t = t1 + t2,
где t1 = 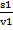 , t2 =
, t2 =  .
.
Задача 1: «Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.»
1) 50*2 + 100 + 2*75 = 350 (км) – путь, пройденный автомобилем;
2) 2 + 1 + 2 = 5 (ч) – время, за которое этот путь пройден;
3) 350: 5 = 70 (км/ч) – средняя скорость автомобиля.
Ответ: 70 км/ч.
Задача 2: «Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.»
Пусть t ч – время, затраченное на дорогу. Тогда:
74*t / 2 + 66*t / 2 = 70t (км) – путь, пройденный автомобилем;
70t / t = 70 (км/ч) – средняя скорость движения.
Ответ: 70 км/ч.
Тренировочные задачи:
1. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 67 км/ч, а вторую половину времени — со скоростью 79 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. (73)
2. Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть – со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. (88)
3. Первые три часа автомобиль ехал со скоростью 70 км/ч, следующий час — со скоростью 65 км/ч, а затем один час — со скоростью 45 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. (64)
4. Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч. (72)
· Задачи на движение протяженных объектов
В задачах на движение протяженных тел часто требуется определить длину одного из них. Наиболее типичные ситуации: определение длины поезда, проезжающего мимо столба или протяженной платформы; параллельное движение двух объектов.
В случае определения длины поезда, проезжающего мимо столба, поезд проходит мимо столба расстояние, равное его длине. В том случае, когда поезд проезжает мимо платформы, он проходит расстояние, равное сумме длин поезда и платформы.
При параллельном движении поездов в одном направлении, удобно принимать скорость одного из поездов, равной нулю. Тогда скорость второго поезда становится равной разности скоростей двух поездов (это относительная скорость). Если в задаче сказано, что поезда двигаются навстречу друг другу, то приняв за ноль скорость одного из них, скорость другого (относительную скорость) найдем сложением скоростей. Тогда решение задачи сводится к решению задачи на нахождение длины поезда, проезжающего мимо платформы. Только в качестве платформы выступает стоящий поезд.
Задача 1: «Поезд, двигаясь равномерно со скоростью 80 км/ч, проезжает мимо придорожного столба за 36 секунд. Найдите длину поезда в метрах»
1) 80 км/ч = 80000 м/ч; 36 с = 0,01ч;
2) 80000*0,01 = 800 (м) – длина поезда.
Ответ: 800 м.
Задача 2: «Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах»
1) 60 км/ч = 60000 м/ч = 1000 м/мин;
2) 1000*1 = 1000 (м) – сумма длин поезда и лесополосы;
3) 1000 – 400 = 600 (м) – длина поезда.
Ответ: 600 м.
Задача 3: «По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах».
1) 90 км/ч = 90000 м/ч = 1500 м/мин;
2) 30 км/ч = 30000 м/ч = 500 м/мин;
3) 1500 – 500 = 1000 (м/мин) – скорость пассажирского поезда, если товарный поезд стоит на месте (относительная скорость);
4) 1000*1 = 1000 (м) – сумма длин товарного и пассажирского поездов;
5) 1000 – 600 = 400 (м) – длина пассажирского поезда.
Ответ: 400 м.
Задача 4: «По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах».
1) 65 км/ч = 65000 м/ч = 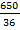 м/с;
м/с;
2) 35 км/ч = 35000 м/ч =  м/с;
м/с;
3) 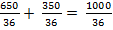 (м/с) – скорость скорого поезда, если пассажирский стоит на месте (относительная скорость);
(м/с) – скорость скорого поезда, если пассажирский стоит на месте (относительная скорость);
4) 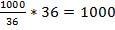 (м) – сумма длин скорого и пассажирского поездов;
(м) – сумма длин скорого и пассажирского поездов;
5) 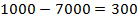 (м) – длина скорого поезда.
(м) – длина скорого поезда.
Ответ: 300 м.
Тренировочные задачи:
1. Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо придорожного столба за 9 секунд. Найдите длину поезда в метрах. (150)
2. Поезд, двигаясь равномерно со скоростью 70 км/ч, проезжает мимо лесополосы, длина которой равна 1000 метров, за 1 минуту 48 секунд. Найдите длину поезда в метрах.
3. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 50 км/ч и 40 км/ч. Длина товарного поезда равна 800 метрам. Найдите длину пассажирского поезда, если время, за которое он прошел мимо товарного поезда, равно 6 минутам. Ответ дайте в метрах. (200)
4. По двум параллельным железнодорожным путям друг навстречу другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 70 км/ч и 50 км/ч. Длина пассажирского поезда равна 800 метрам. Найдите длину скорого поезда, если время, за которое он прошел мимо пассажирского поезда, равно 45 секундам. Ответ дайте в метрах. (700)
Date: 2015-09-02; view: 3607; Нарушение авторских прав