II.Задачи на движение по окружности

Решение задач на движение по окружности в одном направлении точно такое же, как решение задач на движение в одном направлении по прямой. Если два объекта одновременно начинают движение по окружности из одной точки в одну сторону со скоростями v₁ и v₂ соответственно (v₁ > v₂), то первый объект приближается ко второму со скоростью v₁ - v₂ и в момент, когда первый объект в первый раз догоняет второй, он проходит расстояние на один круг больше. И мы имеем дело с формулой, которая ничем не отличается от формулы, полученной для задач на движение вдогонку:

S = (v₁ – v₂) t, где

S – длина окружности;

(v₁ – v₂) –скорость сближения;

t – время, через которое первый объект в первый раз догоняет второй объект.

Задача 1: «Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч».

Так как первый автомобиль через 40 минут после старта опережал второй на один круг, то это значит, что через 40 минут первый автомобиль догнал второй в первый раз. Значит:

1) 40 мин = ч;

2) 14: = 21 (км/ч) – скорость сближения автомобилей;

3) 80 – 21 = 59 (км/ч) – скорость второго автомобиля.

Ответ: 59 км/ч.

Задача 2: «Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 14 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 21 км/ч больше скорости другого?»

В этом случае мотоциклисты начинают движение из разных точек окружности. Так как это диаметрально противоположные точки, то первоначальное расстояние между мотоциклистами рано 7 км. Так как скорость одного из них на 21 км/ч больше скорости другого, то скорость сближения равна 21 км/ч. Значит:

1) 7: 21 = (ч) – время, через которое мотоциклисты поравняются в первый раз;

2) ч = 20 мин.

Ответ: 20 мин.

Задача 3: «Часы со стрелками показывают 8 часов 00 минут. Через сколько минут минутная стрелка в четвертый раз поравняется с часовой?»

Скорость движения минутной стрелки 12 делений/час, а часовой – 1 деление/час (под делением подразумевается расстояние между двумя соседними цифрами на циферблате часов). Так как часы со стрелками показывают 8 часов 00 минут, то первоначальное расстояние между стрелками составляет 8 делений. После того, как минутная стрелка поравняется с часовой в первый раз, она должна будет догнать часовую стрелку еще три раза, то есть обогнать ее на три круга.

1) 12 -1 = 11 (делений/час) – скорость сближения стрелок;

2) 8: 11 = 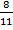(ч) – время, через которое минутная стрелка догонит часовую в первый раз;

3) 12 * 3 = 36 (делений) – длина трех кругов;

4) 36: 11 = 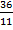(ч) – время, через которое минутная стрелка поравняется с часовой в третий раз после первого;

5) 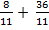= 4 (ч) – время, через которое минутная стрелка в четвертый раз поравняется с часовой;

6)

Ответ: 240 мин.

Тренировочные задачи:

1. Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 30 км. Через сколько минут мотоциклисты поравняются в первый раз, если скорость одного из них на 18 км/ч больше скорости другого? (50)

2. Из одной точки круговой трассы, длина которой равна 10 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 78 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч. (63)

3. Из пункта A круговой трассы выехал велосипедист, а через 30 минут следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч. (80)

4. Часы со стрелками показывают 3 часа ровно. Через сколько минут минутная стрелка в девятый раз поравняется с часовой? (540)

5. Два гонщика участвуют в гонках. Им предстоит проехать 60 кругов по кольцевой трассе протяжённостью 3 км. Оба гонщика стартовали одновременно, а на финиш первый пришёл раньше второго на 10 минут. Чему равнялась средняя скорость второго гонщика, если известно, что первый гонщик в первый раз обогнал второго на круг через 15 минут? Ответ дайте в км/ч. (108)

Date: 2015-09-02; view: 2427; Нарушение авторских прав