Интегрирование некоторых иррациональных функций

Рассмотрим ряд случаев, когда заменой переменной можно свести интегрирование иррациональных функций к интегрированию рациональных функций (т.е., как говорят, рационализировать интеграл).

Прежде всего отметим, что, если подынтегральное выражение содержит только линейную иррациональность то можно использовать подстановку .Так, например, если , то, полагая , имеем .

а) Интегралы вида 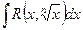, где n – натуральное число. Символ означает рациональную функцию от х и 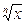. Подстановка 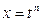(n – общее наименьшее кратное показателей всех радикалов, под которыми х входит в подынтегральную функцию) сводит рассматриваемый интеграл к интегралу рациональной дроби.

Пример 23. Найти .

D Положим . Тогда .

Следовательно,

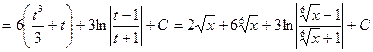. Ñ

б) Интегралы вида , где а, b, с и d – постоянные числа, n –

натуральное число, аd – bс ¹ 0. Функцию вида называют дробно-

линейной иррациональностью. Замена рационализирует интеграл. В самом деле, 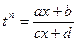, откуда - рациональная функция от t. Далее, .

Поэтому:

где - рациональная функция от t.

Пример 24. Найти .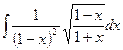

D Полагая 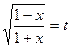, получим , .

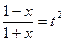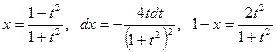Таким образом,

. Ñ

в) Интегралы вида путем выделения полного квадрата из квадратного трехчлена приводятся к рассмотренным выше интегралам (см. примеры 14 и 20 лекция 2).

Пример 25. .

Пример 26. .

г) При вычислении интегралов вида следует предварительно выделить в числителе производную квадратного трехчлена, стоящего под знаком корня , и разложить искомый интеграл на сумму двух интегралов:

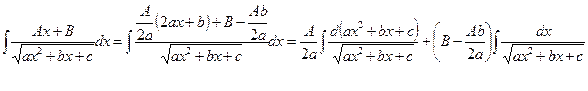Первый интеграл из полученных легко вычисляется при помощи подстановки и равен , а второй рассмотрен в пункте в).

Пример 27. Найти .

D Выделяя в числителе производную подкоренного выражения, получим:

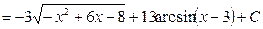. Ñ

д) Интегралы вида 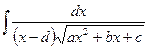с помощью подстановки 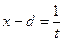приводятся к рассмотренным в пункте в).

Пример 28. Найти .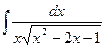

D Полагаем 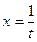, тогда 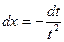. Следовательно,

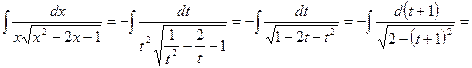
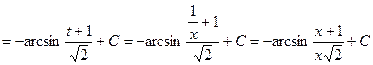. Ñ

е) Интегралы вида , где а, b, с – некоторые числа; ¹ 0; R – рациональная функция от х и от 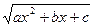. Функцию называют квадратичной иррациональностью.

Если трехчлен имеет вещественные корни х ₁, х ₂ (х₁ ¹ х₂) и а > 0, то

.

Следовательно, ,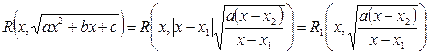

т.е получаем интеграл, рассмотренный в пункте б).

Если х₁ = х_2, то 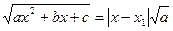, т.е. под знаком интеграла находится

рациональная функция от х. Поэтому будем считать, что не имеет вещественных корней и а > 0. Тогда рационализация интеграла может быть достигнута с помощью подстановки Эйлера:

Отсюда, т.е. - рациональная функция от t.

Следовательно, 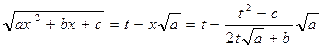- также рациональная функция от t.

Поэтому .

В качестве примера рассмотрим 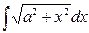, вычисление которого представлено выше (см. лекция 3, пример 10) методом интегрирования по частям.

D Бином не имеет вещественных корней. Поэтому полагаем , , и , .

В силу этого

.

Учитывая, что 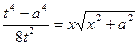, окончательно получаем:

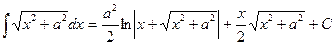. Ñ

Если в трехчлене , а < 0, а с > 0, то для рационализации интеграла можно применить другую подстановку Эйлера:

.

Пример 29. Найти .

Трехчлен имеет комплексные корни и а < 0, с > 0, поэтому воспользуемся подстановкой 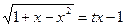. Возводя обе части равенства в квадрат, получаем:

, или .

Отсюда:

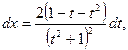
Таким образом,

.

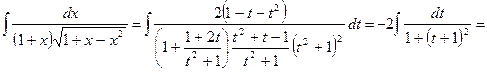
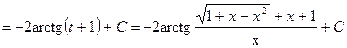Следует отметить, что вычисление интегралов с помощью подстановки Эйлера обычно приводит к громоздким выражениям и трудоемким выкладкам, поэтому их следует применять, только если данный интеграл не удается вычислить более коротким способом.

Применим эйлерову подстановку к вычислению интеграла .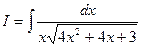

Имеем

.

Значит, .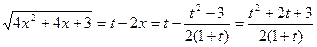

Следовательно,

.

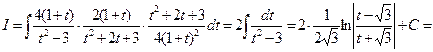
При вычислении интегралов рассматриваемого вида применяются также

искусственные приемы. Рассмотрим в качестве примера интеграл . Полагая получаем 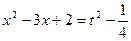. Проводим следующую цепочку преобразований:

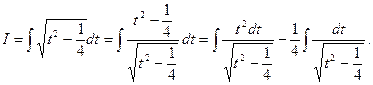
Вычислим интеграл .

Таким образом, имеем:

.

Возвращаясь к исходной переменной x,получаем

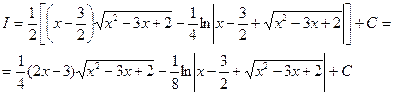
ж) Интегралы вида: 1. 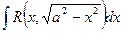, 2. , 3.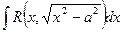

приводятся к интегралам от рациональной относительно 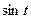и функции с помощью “тригонометрической подстановки”:

для интеграла 1: (или 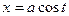), dx=a costdt, ,

для интеграла 2: (или ), ,

для интеграла 3: (или ), .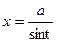

Пример 30. Найти .

D Так как –2 £ х £ 2, то, положив найдем .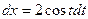

Следовательно,

.

Перейдем в полученном результате снова к переменной х. Имеем:

, , .

Так как 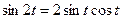, , 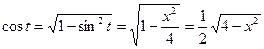то

.

Таким образом,

. Ñ

Отметим, что рассмотренный интеграл можно вычислить и методом интегрирования по частям (см. лекция 3, пример 11).

“Острота зрения” должна подсказывать рациональный путь вычисления интегралов в тех случаях, когда вид подынтегральной функции “подталкивает” к применению кажущейся очевидной подстановки. Так, например, к интегралу не следует применять подстановку 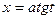,так как .

Date: 2015-09-02; view: 934; Нарушение авторских прав