А) Интегрирование простейших дробей

Лекция 4.

Интегрирование основных классов элементарных функций

Интегрирование рациональных дробей

а) Интегрирование простейших дробей

Рациональной дробью называется дробь вида , где и 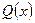- многочлены. Рациональная дробь называется правильной, если степень многочлена ниже степени многочлена 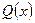; в противном случае дробь называется неправильной. Например, дроби 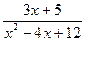, 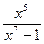- правильные, а дроби 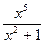, - неправильные.

Простейшими (элементарными) дробями называются правильные дроби следующего вида:

I. ;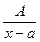

II. , где m – целое число, большее единицы;

III. , где 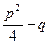<0, т.е. квадратный трехчлен не имеет действительных корней;

IV. , где n – целое число, большее единицы и квадратный трехчлен не имеет действительных корней.

Во всех четырех случаях предполагается, что А, В, p, q, а – действительные числа. Перечисленные дроби будем соответственно называть простейшими дробями I, II, III и IV типов.

Рассмотрим интегралы от простейших дробей.

I. .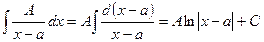

II. 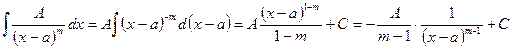, m =2, 3, 4...

Вычислим далее .

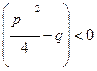Для этого частного случая простейшей дроби IIIтипа получаем:

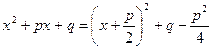, или , где , .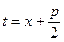

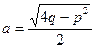Следовательно,

. (*)

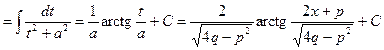Для нахождения интеграла 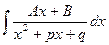( 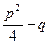<0) выделим в числителе дроби производную знаменателя. Так как , то числитель можно представить в виде .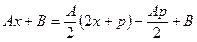

Тогда .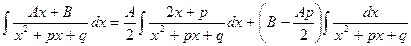

В первом интеграле числитель является производной знаменателя. Поэтому

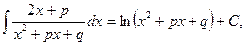т.к. 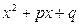>0 для любого значения х.

Учитывая, что второй интеграл, как показано выше, находится по формуле (*), окончательно получаем:

III. .

Покажем теперь в общем виде, как интегрируются простейшие дроби четвертого типа:

IV. .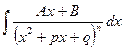

Выделим в числителе производную от квадратного трехчлена в знаменателе:

.

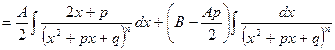Первый интеграл в правой части равенства легко находится при помощи подстановки 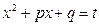, а второй преобразуем так:

.

Полагая 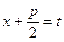, 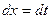и обозначая 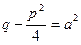, получаем:

.

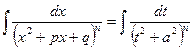Для интеграла (n – целое положительное число), имеет место следующая рекуррентная формула:

. (**)

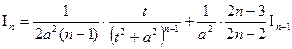(В частном случае, при а =1 ее вывод представлен выше).

Эта формула в результате (n -1)-кратного применения приводит данный интеграл I _n к табличному интегралу .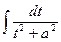

Рассмотрим примеры.

Пример 1. Найти .

D Дискриминант квадратного трехчлена, стоящего в знаменателе, отрицателен: <0, т.е. имеем интеграл III типа. Так как , то числитель дроби преобразуем следующим образом: .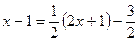

Поэтому .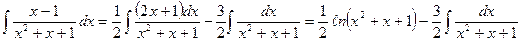

Оставшийся интеграл находим выделением полного квадрата в квадратном трехчлене:

.

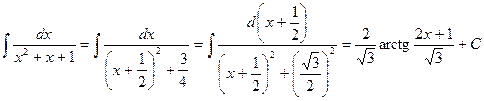В результате заданный интеграл равен

. Ñ

Пример 2. Найти .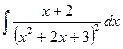

D Здесь 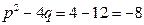< 0, т.е. имеем интеграл IV типа. Сначала выделим в числителе производную квадратного трехчлена. Так как , то числитель преобразуется следующим образом: .

Далее имеем: .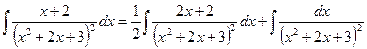

Первый интеграл вычисляем, положив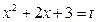

.

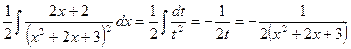Для вычисления оставшегося интеграла приведем его к стандартному виду, выделяя полный квадрат в квадратном трехчлене:

.

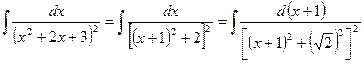Используя рекуррентную формулу (**), находим:

.

Окончательно получаем:

. Ñ

Date: 2015-09-02; view: 664; Нарушение авторских прав