Частные подстановки

Универсальная подстановка 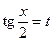во многих случаях приводит к сложным вычислениям, так как при ее применении и выражаются через t в виде рациональных дробей, содержащих .

В указываемых ниже случаях предпочтительнее следующие частные подстановки, также рационализирующие интеграл.

а*) Если - нечетная функция относительно , т.е. , то интеграл рационализируется подстановкой .

Пример 11. Найти .

D Полагая , найдем , , .

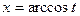Поэтому

. Ñ

Можно было бы избежать выражения и через t, проведя следующие

преобразования:

.

б*) Если функция нечетная относительно косинуса, т.е. 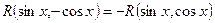, то применима подстановка .

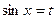Пример 12. Найти .

D Полагаем 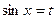. При этом ,

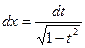
Ñ

Рассмотренный интеграл можно преобразовать, подведя под знак дифференциала, после чего воспользоваться подстановкой .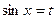

.

в*) Если - четная функция относительно и , т.е., если , то к цели приводит подстановка .

Пример 13. Найти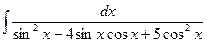

D Полагаем . Тогда , , , .

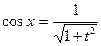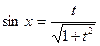Имеем

. Ñ

К выводу о целесообразности применения подстановки можно придти, разделив в исходном интеграле числитель и знаменатель на :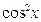

.

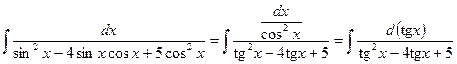Пример 13а. Найти .

.

Отметим, что подстановка x=tgt может быть применена к некоторым интегралам от рациональных дробей.

Вычислим с помощью этой подстановки интеграл 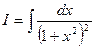, рассмотренный в конце лекции3.

Имеем:

.

Учитывая, что t=arctg x, приходим к ответу: .

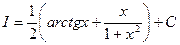Хотя частные подстановки, когда они применимы, обычно приводят к более простым выкладкам, чем универсальная подстановка, однако в ряде случаев она обеспечивает кратчайший путь. Поэтому при выборе подстановки нужна известная осмотрительность.

Пример 14. Найти .

D Так как подынтегральная функция нечетна относительно синуса, то применима подстановка 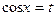. При такой подстановке получим:

.

Таким образом, приходим к не очень простому интегралу рациональной дроби.

Попробуем универсальную подстановку 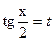. Тогда , , и получаем

. Ñ

Универсальная подстановка оказалась предпочтительнее.

б) Интегралы вида .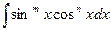

Выделим три случая, имеющие особенно важное значение.

Случай 1. Если, по крайней мере, один из показателей m или n, нечетное положительное число, то, отделяя от нечетной степени один сомножитель и выражая с помощью формулы оставшуюся четную степень через дополнительную функцию, приходим к табличному интегралу. Таким образом, в этом случае интеграл берется непосредственно.

Пример 15. Найти .

D Здесь показатель степени косинуса равен трем, поэтому делаем подстановку 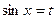, . Тогда:

. Ñ

Случай 2. Оба показателя степени m и n – четные положительные числа.

Применение формул , , позволяет повторным уменьшением вдвое показателей степеней синуса и косинуса свести рассматриваемые интегралы к легко вычисляемым.

Пример 16. Найти .

D Имеем

Ñ

Случай 3. Если m + n является целым четным отрицательным числом, то целесообразно использовать подстановку или .

Пример 17. Найти .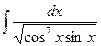

D Здесь m + n = . Поэтому вычисление интеграла сводится к интегрированию степеней тангенса:

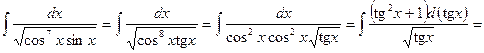
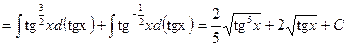. Ñ

В общем случае интегралы вида 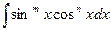, где m и n - целые числа, вычисляются с помощью рекуррентных формул, которые, как показано выше, выводятся путем интегрирования по частям.

В частности, интегралы от нечетной положительной степени секанса или косеканса проще всего находятся по рекуррентным формулам:

,

.

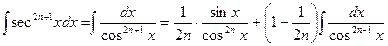Выведем рекуррентную формулу для и с ее помощью найдем .

Имеем: .

Для вычисления первого интеграла применяем формулу интегрирования по частям:

Отсюда получаем:

Итак, интеграл выражен через : .

В частности, при n = 1 имеем: .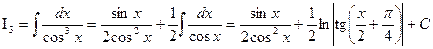

в) В теории рядов Фурье важное значение имеют интегралы

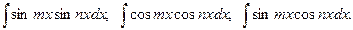
Тригонометрические формулы:

,

,

,

дают возможность произведение тригонометрических функций представить в виде суммы.

Пример 18. Найти .

D Имеем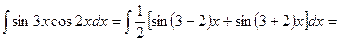

. Ñ

Пример 19. =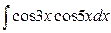

.

Date: 2015-09-02; view: 441; Нарушение авторских прав