
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Гипербола
|
|
Гиперболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
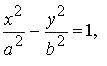
где a > 0, b > 0 — параметры гиперболы.
Это уравнение называется каноническим уравнением гиперболы, а система координат, в которой гипербола описывается каноническим уравнением, называется канонической.
В канонической системе оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.
Точки пересечения гиперболы с осью OX (± a, 0) называются вершинами гиперболы.
С осью OY гипербола не пересекается.
Отрезки a и b называются полуосями гиперболы.
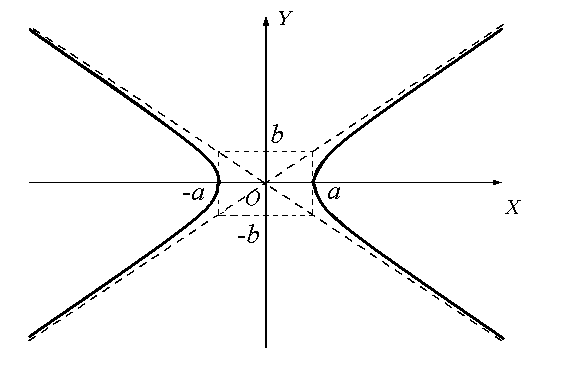
Рис.1
Прямые ay − bx = 0 и ay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность, соответствующая ветвь гиперболы приближается к одной из асимптот.
Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b).
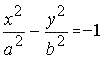
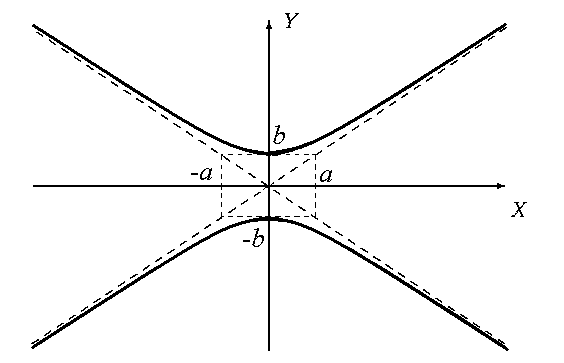
Рис.2
Такая гипербола называется сопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0. Говорят о паре сопряжённых гипербол.
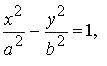
Date: 2015-08-24; view: 685; Нарушение авторских прав