Поток энергии в волновых процессах

В процессе распр волн в упр среде происх перенос энергий колебаний. Рассм плоск волну распр вдоль оси Х. ∆V=∆S∆l; ∆t→∆V найжем кин энерг колеб этих частиц. ∆W=W∆V=W∆SV∆t. Найжем кин энерг перенос-ю через пов-ть ∆S за ед времени-поток энергии. P=∆W/∆t=WV∆ρ. Найдем энергию перенос-ю волной за ед времени через ед пов-ть т.е. плотность потока энергии u=∆W/∆S∆t=WV. u = WV. u↑ ↑ V. u -вектор Умова. Вектор умова х-т энергию перенос волной за ед времени ч/з ед пов-ть расп перп к напр распр-я волны.

u=[Вт/м²]

54. Если в среде распространяется несколько волн, то колебания частиц среды оказываются геометрической суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Волны накладываются друг на друга, не возмущая (не искажая друг друга). Это и есть принцип суперпозиции волн.

Если две волны, приходящие в какую-либо точку пространства, обладают постоянной разностью фаз, такие волны называются когерентными. При сложении когерентных волн возникает явление интерференции.

Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении от преград.

Напишем уравнения двух плоских волн, распространяющихся в противоположных направлениях (начальная фаза ):

.

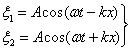(5.5.1)

Сложим уравнения и преобразуем по формуле суммы косинусов (5.4.3):

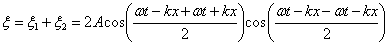Т.к. 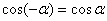, то можно записать:

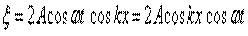Учитывая, что 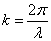, получим уравнение стоячей волны:

.

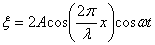(5.5.2)

В выражении для фазы не входит координата, поэтому можно записать:

,

(5.5.3)

где суммарная амплитуда . В точках, где координаты удовлетворяют условию 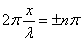(n = 1, 2, 3, …), 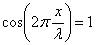, суммарная амплитуда равна максимальному значению: 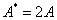, – это пучности стоячей волны. Координаты пучностей:

.

(5.5.4)

В точках, координаты которых удовлетворяют условию (n = 0, 1, 2,…), 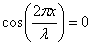и суммарная амплитуда колебаний равна нулю , – это узлы стоячей волны. Координаты узлов:

.

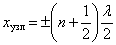(5.5.5)

Точки среды, находящиеся в узлах, колебаний не совершают.

Образование стоячих волн наблюдают при интерференции бегущей и отраженных волн. На границе, где происходит отражение волны, получается пучность, если среда, от которой происходит отражение, менее плотная (рис. 5.5, а), и узел – если более плотная (рис. 5.5, б).

Если рассматривать бегущую волну, то в направлении ее распространения переносится энергия колебательного движения. В случае же стоячей волны переноса энергии нет, т.к. падающая и отраженная волны одинаковой амплитуды несут одинаковую энергию в противоположных направлениях.

 

 

Date: 2015-08-24; view: 657; Нарушение авторских прав