
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задачи для подготовки к контрольной работе
|
|
1. В ящике 5 белых и 8 черных шаров. Из ящика вынули три шара, не возвращая вынутый шар в ящик. Найти вероятность того, что все три шара белые.
2. 25% населения земного шара европеоиды, 35% монголоиды, остальные негроиды. Среди европеоидов 30% людей имеют карие глаза, среди монголоидов 90%, среди негроидов 95%. Какова вероятность того, что наугад выбранное лицо имеет карие глаза?
3. В урне 7 белых и 3 черных шара. Вынули подряд 5 шаров, причем каждый шар возвращают в урну и шары в урне перемешивают. Какова вероятность того, что из этих 5 шаров 3 шара окажутся белыми?
4. В магазин поступает один и тот же товар, изготовленный на трех фабриках, причем первая фабрика поставляет 55% от общего числа изделий, вторая 20%, а третья 25%. Вероятность бракованного товара, поступающего с этих фабрик, соответственно равна 0,1; 0,3; 0,2. Найти вероятность того, что оказавшееся бракованным изделие изготовлено на первой фабрике.
5. Вероятность того, что мяч попадет в корзину при одном бросании, равна 0,7. Какова вероятность того, что при 7 бросаниях мяч попадет в корзину хотя бы один раз?
6. Задана непрерывная случайная величина X своей функцией распределения F(x). Вычислить математическое ожидание и дисперсию случайной величины X, если
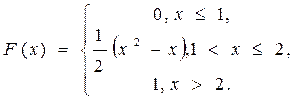
7. Задана непрерывная случайная величина X своей плотностью распределения вероятностей f(x). Требуется: 1) определить коэффициент A; 2) найти вероятность того, что случайная величина X примет значение из интервала (a,b), если 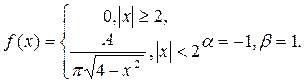
8. Задана непрерывная случайная величина X своей плотностью распределения вероятностей f(x). Требуется: 1) определить коэффициент A; 2) найти функцию распределения F(x), если
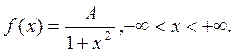
9. Задана непрерывная случайная величина X своей функцией распределения F(x). Найти вероятность того, что случайная величина X примет значение, меньшее своего математического ожидания, если
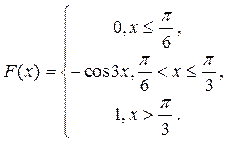
10. Случайная величина X характеризуется рядом распределения
| xi | ||||
| pi | 0,4 | 0,3 | 0,2 | 0,1 |
Найти M(X), D(X), s(X).
11. Путем опроса получены следующие данные о возрасте (числе полных лет) 25 студентов второго курса:
18 17 23 18 17 19 18 20 17 22 19 21
18 18 17 22 18 21 17 21 18 19 17 23 17
Составить вариационный ряд выборки, вычислить средневыборочное и выборочную дисперсию.
12. В урне 4 белых, 7 черных, 5 синих и 3 красных шара. Вынули один шар. Найти вероятность того, что вынутый шар белый или синий.
13. Вероятность поражения цели первым стрелком равна 0,7, вторым – 0,75, третьим – 0,8. Какова вероятность того, что цель будет поражена?
14. 25% населения земного шара – европеоиды, 35% – монголоиды, остальные – негроиды. Среди европеоидов 30% людей имеют карие глаза, среди монголоидов – 90%, среди негроидов – 95%. Какова вероятность того, что лицо с карими глазами является монголоидом?
15. В магазин поступает один и тот же товар, изготовленный на трех фабриках, причем первая фабрика поставляет 55% от общего числа изделий, вторая 20%, а третья 25%. Вероятность бракованного товара, поступающего с этих фабрик, соответственно равна 0,1; 0,2; 0,25. Найти вероятность того, что оказавшееся бракованным изделие изготовлено на второй фабрике.
16. Вероятность того, что мяч попадет в корзину при одном бросании равна 0,3. Какова вероятность того, что при 5 бросаниях мяч попадет в корзину не более 2 раз?
17. Задана непрерывная случайная величина X своей плотностью распределения вероятностей f(x). Вычислить математическое ожидание и дисперсию случайной величины X, если
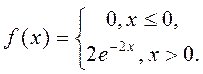
18. В первом ящике 4 белых и 3 черных шара; во втором ящике 5 белых и 3 черных шара. Из каждого ящика вынули по шару. Какова вероятность того, что оба шара белые?
Варианты контрольной работы
Вариант А
1. Среди 13 изделий 6 бракованных. Найти вероятность того, что среди 4 изделий окажется 2 бракованных.
2. В ящике 3 белых и 10 черных шаров. Из ящика вынули три шара, не возвращая вынутый шар в ящик. Найти вероятность того, что все три шара черные.
3. 25% населения земного шара – европеоиды, 35% – монголоиды, остальные – негроиды. Среди европеоидов 30% имеют карие глаза, среди монголоидов – 90%, среди негроидов – 95%. Какова вероятность того, что лицо с не карими глазами является монголоидом?
4. Вероятность того, что мяч попадет в корзину при одном бросании равна 0,75. Какова вероятность того, что при 5 бросаниях мяч попадет в корзину не менее 4 раз?
5. Задана непрерывная случайная величина X своей функцией распределения F(x).
Требуется:
1) определить коэффициент A;
2) найти плотность распределения вероятностей f(x);
3) вычислить математическое ожидание и дисперсию случайной величины X;
4) найти вероятность того, что случайная величина X примет значение из интервала (α,β), если

Вариант Б
1. Среди 12 монет 4 фальшивых. Найти вероятность того, что среди 5 монет окажутся 2 фальшивые.
2. В первом ящике 2 белых и 8 черных шаров; во втором ящике 5 белых и 8 черных шаров. Из каждого ящика вынули по шару. Какова вероятность того, что оба вынутые шара черные?
3. В магазин поступает один и тот же товар, изготовленный на трех фабриках, причем первая фабрика поставляет 30% от общего числа изделий, вторая 40%, а третья 30%. Вероятность бракованного товара, поступающего с этих фабрик, соответственно равна 0,1; 0,2; 0,15. Найти вероятность бракованного изделия среди наугад выбранного.
4. В урне 7 белых и 3 черных шара. Вынули подряд 5 шаров, причем каждый вынутый шар возвращают в урну и шары в урне перемешивают. Какова вероятность того, что из этих 5 шаров 3 шара окажутся белыми?
5. Задана непрерывная случайная величина X своей плотностью распределения f(x).
Требуется:
1) определить коэффициент A;
2) найти функцию распределения F(x);
3) вычислить математическое ожидание и дисперсию случайной величины X;
4) найти вероятность того, что случайная величина X примет значение из интервала (α,β), если
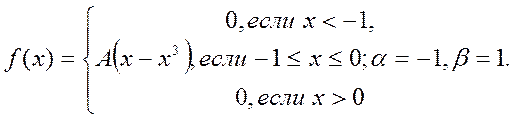
Ответы к вариантам контрольной работы
| Вариант А | Вариант Б | ||
| 
| ||
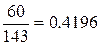
| 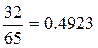
| ||
| 0.1522 | 0.155 | ||
| 0.6328 | 0.3087 | ||
| A | –4 | ||
| M(X) | 
| 
| |
| D(X) | 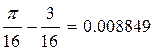
| 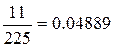
| |
| P(α<X<β) | 
|
ВОПРОСЫ для подготовки к зачету [3]
1. Событие. Сумма и произведение событий. Противоположные события.
2. Несовместные события. Полная группа несовместных событий.
3. Классическое определение вероятности. Аксиомы вероятности.
4. Геометрическое определение вероятности. Примеры.
5. Теорема сложения вероятностей в случае несовместных событий.
6. Теорема сложения вероятностей в случае совместных событий.
7. Независимые события. Условная вероятность события.
8. Теорема умножения вероятностей в случае независимых событий.
9. Теорема умножения вероятностей в случае зависимых событий.
10. Формула полной вероятности.
11. Формула Байеса.
12. Схема повторных испытаний. Формула Бернулли.
13. Наивероятнейшее число наступления события.
14. Случайные величины дискретного типа. Функция распределения и ее свойства.
15. Математическое ожидание случайной величины дискретного типа и его свойства.
16. Дисперсия случайной величины дискретного типа и ее свойства.
17. Случайные величины непрерывного типа. Функция распределения, плотность распределения и их свойства.
18. Математическое ожидание случайной величины непрерывного типа и его свойства.
19. Дисперсия случайной величины непрерывного типа и ее свойства.
20. Равномерное распределение случайных величин.
21. Биномиальное распределение случайных величин.
22. Распределение Пуассона.
23. Экспоненциальное распределение случайных величин.
24. Нормальное распределение случайных величин.
25. Функция Лапласа и ее свойства.
26. Вероятность попадания в интервал нормально распределенной случайной величины. Правило трех сигм.
Содержание
Линейная алгебра. 3
Математический анализ. 4
Теория вероятностей и математическая статистика. 4
С о с т а в и т е л ь В. Н. Величкин
Учебно-методический комплекс
дисциплинам
Линейная алгебра,
Математический анализ,
Теория вероятностей
и математическая статистика
для направления подготовки 080100 Экономика
Квалификация (степень) выпускника «бакалавр»
Редактор Л.А. Юрганова
Компьютерная верстка О.А. Гришина
____________________________________________________________________ Подписано в печать 28.03.2011. Формат 60х90/16
Объем 2 п.л. Тираж 500 экз.
Институт международного права и экономики имени А.С. Грибоедова
105066, Москва, Новая Басманная ул., д. 35, стр. 1
[1] Уточняются и дополняются в каждом учебном году.
[2] Уточняются и дополняются в каждом учебном году.
[3] Уточняются и дополняются в каждом учебном году.
Date: 2015-08-24; view: 609; Нарушение авторских прав