
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задачи для подготовки к контрольной работе. 1. Найти в градусах угол между прямыми, уравнения которых
|
|
1. Найти в градусах угол между прямыми, уравнения которых
х + 2у – 5 = 0,
2х – у + 4 = 0.
2. Найти в градусах угол между прямыми, уравнения которых
5х – у + 7 = 0,
2х – 3у + 3 = 0.
3. Какова площадь треугольника, отсекаемого от осей системы координат прямой, проходящей через точки А(4;5) и В(–2;–10)?
4. Какова площадь треугольника, отсекаемого от осей системы координат прямой, проходящей через точки А(0;–4) и В(1;–2)?
5. Найти координаты центра окружности, описанной около треугольника, вершины которого находятся в точках А(3;–2), В(–3;0), С(1;4).
6. Найти координаты центра окружности, описанной около треугольника, вершины которого находятся в точках А(0;1), В(4;–3), С(2;3).
7. Найти длину высоты треугольника АВС, проведенной из вершины А, если А(–1;–3), В(–9;–7), С(–1;–1).
8. Найти длину высоты треугольника АВС, проведенной из вершины А, если А(0;–1), В(1;1/2), С(–5;–2).
9. Найти в градусах угол между плоскостями, уравнения которых
х – 2у + 2z – 8 = 0,
х + z – 3 = 0.
10. Найти в градусах угол между плоскостями, уравнения которых
3х – 2у + z + 5 = 0,
х + у – z + 4 = 0.
11. Каков объем пирамиды, осекаемой от координатного угла плоскостью, проходящей через точки А(0;2;–1), В(3;4;2), С(–3;8;0)?
12. Найти проекцию вектора а = {4;–2;2} на вектор b = { 0;0;10}.
13. Найти проекцию вектора а = {0;–1;4} на вектор b = {2;–2;1}.
14. Найти проекцию вектора а = {1;2;3} на вектор b = {0;–3;4}.
15. Найти проекцию вектора а = {–1;3;5} на вектор b = {5;0;–12}.
16. При каком значении параметра а прямые, уравнения которых
(а + 2)х – 2у + 3 = 0,
3х + (а –3)у + 5 = 0,
будут параллельны?
17. При каком значении параметра а прямые, уравнения которых
(а– 6)х – 3у + 7 = 0,
2х + (а –1)у + 5 = 0,
будут параллельны?
18. При каком значении параметра а прямые, уравнения которых
(За + 2)х + (1 – 4 а)у +8 = 0,
(5 а – 2)х + (а + 4)у – 7 = 0,
будут перпендикулярны?
19. При каком значении параметра а прямые, уравнения которых
(За + 1)х + (а – 3)у + 2 = 0,
(5а – 1)х + (5а + 3)у – 1 = 0,
будут перпендикулярны?
20. Найти длину высоты пирамиды АВСD, опущенной из вершины D, если
А(–4;2;6), В(2;–3;0), С(–10;5;8), D(–5;2;–4).
21. Найти длину высоты пирамиды АВСD, опущенной из вершины D, если
А(2;3;1), В(4;1;–2), С(6;3;7), D(7;5;–3).
22. Найти длину высоты пирамиды АВСD, опущенной из вершины D, если
А(3;10;–1), В(–2;3;–5), С(–6;0;–3), D(1;–1;2).
23. Найти длину высоты пирамиды АВСВ, опущенной из вершины D, если
А(–1;2;4), В(–1;–2;–4), С(3;0;–1), D(7;–3;1).
24. Даны уравнения четырех граней тетраэдра АВСD:
(АВС): х – 2у + z – 5 = 0, (АВD): 2х – у +3z – 9 = 0,
(ВСD): 3у – z + 5 = 0, (АСD): 2х – 2у + z – 9 = 0.
Найти длину высоты этого тетраэдра, опущенной из вершины В.
25. Даны уравнения четырех граней тетраэдра АВСD:
( АВС ): х + 2у – z – 5 = 0, ( АВD ): Зх + 4z – 1 = 0,
( ВСD ): 2х – у + 5z + 4 = 0, ( АСD ): х – 2у + 2z + 7 = 0.
Найти длину высоты этого тетраэдра, опущенной из вершины В.
26. Найти расстояние от точки А(0;1;–2) до плоскости, которая проходит через точку В(1;3;–5) и параллельна плоскости, имеющей уравнение
2х + 2у – z + 1 = 0.
27. Найти расстояние от точки А(1;–1;5) до плоскости, которая проходит через точку В(2;–3;0) и параллельна плоскости, имеющей уравнение
х – 2у – 2z + 7 = 0.
28. Вычислить в градусах угол между прямой  и плоскостью
и плоскостью
х – 2у – 2z + 3 = 0.
29. Вычислить в градусах угол между прямой 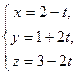 и плоскостью
и плоскостью
x+z–3=0.
30. Вычислить в градусах угол между прямой 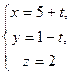 и плоскостью
и плоскостью
x–z+7=0.
31. Найти координаты точки D' – проекции точки D на плоскость, проходящую через точки А, В, С, если
А(–1;–5;2), В(–6;0;–3), С(3;6;–3), D(–10;6;7).
32. Найти координаты точки D' – проекции точки D на плоскость, проходящую через точки А, В, С, если
А(5;2;0), В(2;5;0), С(1;2;4), D(–1;1;1).
33. Найти координаты точки D' – проекции точки D на плоскость, проходящую через точки А, В, С, если
А(2;–1;–2), В(1;2;1), С(5;0;–6), D(–10;9;–7).
34. Найти координаты точкиD' – проекции точки D на плоскость, проходящую через точки А,В, С, если
А(–2;0;–4), В(–1;7;1), С(4;–8;–4), D(1;–4;6).
35. Найти координаты точки D' – проекции точки D на плоскость, проходящую через точки А, В, С, если
А(14;4;5), В(–5;–3;2), С(–2;–6;–3), D(–2;2;–1).
36. Найти координаты точки D' – проекции точки D на плоскость, проходящую через точки А, В, С, если
А(2;–1;2), В(1;2;–1), С(3;2;1), D(–4;2;5).
37. Найти координаты точки D' – проекции точки D на плоскость, проходящую через точки А, В, С, если
А(1;1;2), В(–1;1;3), С(2;–2;4), D(–1;0;–2).
38. Найти координаты точки D' – проекции точки D на плоскость, проходящую через точки А, В, С, если
А(–1;2;–3), В(4;–1;0), С(2;1;–2), D(3;4;5).
39. Найти координаты точки D' – проекции точки D на плоскость, проходящую через точки А, В, С, если
А(4;–1;3), В(–2;1;0), С(0;–5;1), D(3;2;–6).
40. Найти координаты точкиD' – проекции точки Dна плоскость, проходящую через точки А, В, С, если
А(1;2;0), В(1;–1;2), С(0;1;–1), D(–3;0;1).
41. Построить линию и найти ее эксцентриситет
3х2 + 4у2 + 6х – 16у + 7=0.
42. Построить линию и найти ее эксцентриситет
3х2 + 4у2 – 6х + 8у – 5 = 0.
43. Построить линию и найти ее эксцентриситет
9х2 + 25у2 + 18х – 50у – 191 =0.
44. Построить линию и найти ее эксцентриситет
9х2 + 25у2 – 100у – 125=0.
45. Построить линию и найти ее эксцентриситет
5х2 – 4у2 + 10х – 24у – 51 =0.
46. Построить линию и найти ее эксцентриситет
5х2 – 4у2 – 10х – 15=0.
47. Построить линию и найти ее эксцентриситет
3х2 – у2 + 6х + 4у – 4= 0.
48. Построить линию и найти ее эксцентриситет
3х2 – у2 + 6х – 2у – 1 = 0.
49. Построить линию и найти ее эксцентриситет
24х2 + 48х + 25у2 = 0.
50. Построить линию и найти ее эксцентриситет
4х2 – 5у2 – 4х – 10у + 16 = 0.
51. Построить линию и найти ее эксцентриситет
144х2 – 25у2 – 50у + 3575 = 0.
Варианты контрольной работы
Вариант А
1. Найти длину высоты треугольника АВС, проведенной из вершины А, если А(–1;–3), В(–9;–7), С(–1;–1).
2. Какова площадь треугольника, отсекаемого от осей системы координат прямой, проходящей через точки А(0;–4) и В(1;–2)?
3. Вычислить в градусах угол между прямой  и плоскостью
и плоскостью
х – 2у – 2z + 3 = 0.
4. Найти координаты точки D' – проекции точки D на плоскость, проходящую через точки А, В, С, если
А(14;4;5), В(–5;–3;2), С(–2;–6;–3), D(–2;2;–1).
5. Построить линию и найти ее эксцентриситет
4х2 – 5у2 – 4х – 10у + 16 = 0.
Вариант Б
1. Найти длину высоты треугольника АВС, проведенной из вершины А, если А(0;–1), В(1;1/2), С(–5;–2).
2. Каков объем пирамиды, осекаемой от координатного угла плоскостью, проходящей через точки А(0;2;–1), В(3;4;2), С(–3;8;0)?
3. Вычислить в градусах угол между прямой  и плоскостью
и плоскостью
2х + y –z + 7 = 0.
4. Найти координаты точки D' – проекции точки D на плоскость, проходящую через точки А, В, С, если А(2;–1;–2), В(1;2;1), С(5;0;–6), D(–10;9;–7).
5. Построить линию и найти ее эксцентриситет
144х2 – 25у2 – 50у + 3575 = 0.
Вариант В
1. Найти площадь треугольника с вершинами в точках А(2;–1), В(5;1) С(3;5).
2. При каком значении параметра а прямые, уравнения которых
(а + 1)х + (а – 6)у + 7 = 0,
(3 а + 2)х + (2 а + 2)у – 3 = 0,
будут перпендикулярны?
3. Даны уравнения четырех граней тетраэдра АВСD:
(АВС): 3х – у + z + 5 = 0, (АВD): х + у + 2z = 0,
(ВСD): 2х + у + 3z + 2 = 0, (АСD): х + 2у – 2z – 2 = 0.
Найти длину высоты этого тетраэдра, опущенной из вершины В.
4. Найти координаты точки D' – проекции точки D на плоскость, проходящую через точки А, В, С, если А(–2;0;–4), В(–1;7;1), С(4;–8;–4), D(1;–4;6).
5. Построить линию и найти ее эксцентриситет
16х2 – 9у2 + 96х + 36у + 252 = 0.
Ответы к вариантам контрольной работы
| Вариант А | 1,6 | –1;–2;2 | 1,5 | ||
| Вариант Б | 2;5;1 | 2,6 | |||
| Вариант В | 2; –1 | 5;–1;1 | 1,25 |
ВОПРОСЫ для подготовки к экзамену [1]
1. Определители и их основные свойства.
2. Миноры и алгебраические дополнения. Разложение определителя по элементам строки (столбца).
3. Правило Крамера.
4. Матрицы и действия над ними (сложение матриц, умножение матрицы на число).
5. Умножение матриц.
6. Обратная матрица и ее нахождение.
7. Матричная запись системы линейных уравнений и ее решение с помощью обратной матрицы.
8. Ранг матрицы. Эквивалентность двух определений ранга матрицы.
9. Нахождение ранга матрицы с помощью элементарных преобразований.
10. Исследование системы линейных уравнений. Теорема Кронекера – Капелли.
11. Системы линейных однородных уравнений. Фундаментальная система решений.
12. Собственные векторы и собственные значения матрицы.
13. Квадратичные формы. Приведение квадратичной формы к каноническому виду.
14. Линейные операции над векторами и их координатная запись.
15. Скалярное произведение векторов и его свойства.
16. Скалярное произведение в координатах.
17. Векторное произведение векторов и его свойства.
18. Векторное произведение в координатах.
19. Смешанное произведение векторов и его свойства.
20. Смешанное произведение в координатах.
21. Параметрические и канонические уравнения прямой линии на плоскости.
22. Уравнение прямой линии на плоскости, проходящей через две заданные точки.
23. Уравнение прямой с угловым коэффициентом. Общее уравнение прямой линии на плоскости.
24. Угол между двумя прямыми на плоскости. Условие перпендикулярности двух прямых на плоскости.
25. Расстояние от точки до прямой (на плоскости).
26. Уравнение плоскости, проходящей через три заданные точки.
27. Общее уравнение плоскости и его исследование.
28. Угол между двумя плоскостями.
29. Параметрические и канонические уравнения прямой линии в пространстве.
30. Угол между двумя прямыми в пространстве.
31. Угол между прямой и плоскостью.
32. Расстояние от точки до прямой (в пространстве).
33. Расстояние между двумя прямыми (в пространстве).
34. Эллипс как линия второго порядка.
35. Гипербола как линия второго порядка.
36. Параллельный перенос осей системы координат.
37. Исследование общего уравнения линии второго порядка, не содержащего произведения неизвестных.
Date: 2015-08-24; view: 572; Нарушение авторских прав