Высвобождающая единица как самоподдерживающийся кальциевый осциллятор

В программном комплексе, разработанном на базе рассматриваемой модели, исследовалась динамика ионов Са²⁺ в высвобождающая единице, включающей в себя кластер 9х9 RyR-каналов. Как уже отмечалось, процессы открытия/закрытия каналов в течение кальциевого цикла носят стохастический характер, и вероятность их открытия зависит от концентраций Са²⁺ в люмене СР и диадном пространстве. Из этого следует, что их активность должна меняться в течение Са²⁺-цикла в клетке.

Данный программный комплекс позволил исследовать внутренние Са²⁺-«часы» и получить временные зависимости таких величин, как концентрация Са²⁺ в люмене (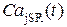), эффективное давления (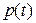), концентрация Са²⁺ в диадном пространстве (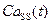), концентрация Са²⁺ в цитозоле клетки (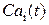) и число открытых каналов в кластере (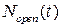). Подробно предположительный цикл работы кальциевых «часов» описан ранее в пункте 3.2.4 настоящей работы.

На рисунке 4.9 представлены результаты численного моделирования Са²⁺-«часов» при следующих значениях параметров динамики 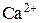: 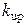=0.0012 М·с^-1, = 6·10^-7 М, 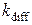= 25·10³ с^-1, = 50 с^-1, 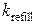=1 с^-1. Параметры концентраций буферов, учитывающихся в модели, выбирались согласно работе [80]: CQ _tot = 10^-2 М, CM _tot = 45·10^-6 М, TC _tot = 31·10^-6 М.

На данном этапе моделирование проводилось без учета конформационного взаимодействия между RyR-каналами в решетке (k =0). Параметры ЭК модели (2.5-2.8) выбирались такими же, как и в работе [A1]: a = 5, K = 12, 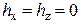, Г = 7, n = 6, 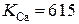·10^{-6 M}. Параметры туннелирования: A = 1, 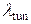= 0.01.

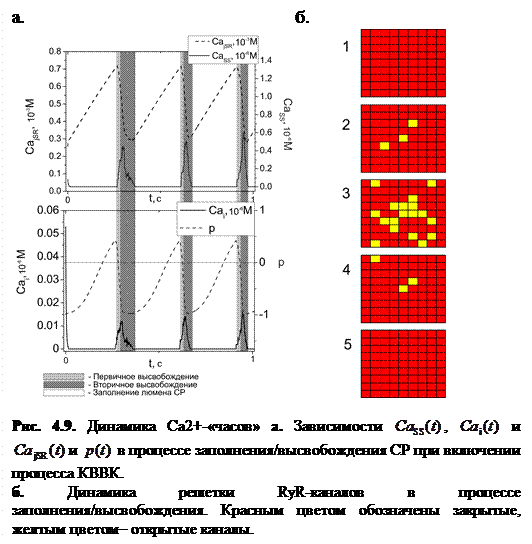
Как видно из рисунка, Са²⁺- высвобождающая единица действительно ведет себя как самоподдерживающийся осциллятор в определенном диапазоне динамических параметров.

Зависимость 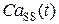представляет собой последовательность отдельных сигналов несинусоидальной формы с практически постоянной амплитудой (0.5±0.075 мкМ). На основании этого можно сделать вывод, что высвобождающая единица при данном значении динамических параметров ведет себя как релаксационный осциллятор. Число открытых каналов также меняется периодически. В начале эксперимента все каналы решетки закрыты (рис. 4.9б(1)), затем происходит открытие малого числа каналов, вызывая тем самым первичное высвобождение (рис. 4.9б(2)). Затем открывается большее число каналов (рис. 4.9б(3)), в связи с чем резко понижается концентрация 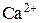в люмене, что стимулирует перезагрузку системы и закрытие каналов (рис. 4.9б(4, 5)). Высвобожденный кальций диффундирует сначала в цитозоль, затем возвращается в сеть ретикулума. После этого в процессе заполнения 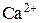попадает обратно в люмен, и процесс высвобождения повторяется.

Отличительной особенностью релаксационного осциллятора является независимость его кинетических параметров от начальных условий [124, 125]. Для проверки этого эффекта построены зависимости и в повторяющемся цикле работы Са²⁺-«часов» при различных начальных условиях (рис. 4.10).

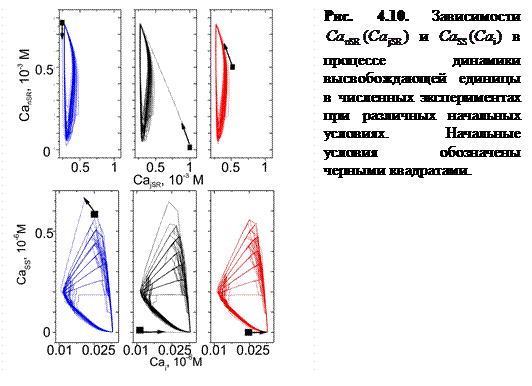
Из графиков ясно, что выбор начальных условий не влияет на характер дальнейшей динамики системы, что подтверждает устойчивость релаксационных колебаний осциллятора при данных значениях параметров.

4.2.2 Моды динамики Са²⁺-«часов»

Важно отметить, что в ходе моделирования при варьировании параметра 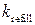и при учете кооперативной динамики RyR-каналов были выявлены и другие типы колебаний внутренних Са²⁺-«часов».

На рисунке 4.11 изображены зависимости концентрации Са²⁺ в диадном пространстве от времени при различных значениях параметра скорости заполнения люмена.

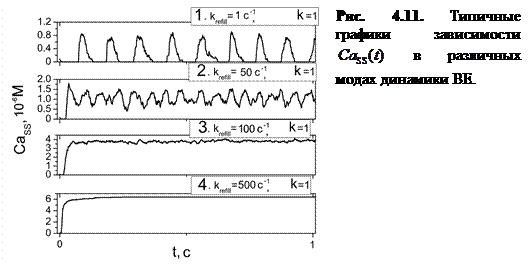
При варьировании параметра 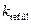в широком диапазоне (0.05÷500 мс^-1) выявлено пять основных мод динамики высвобождающей единицы, которые подробно будут описаны далее.

В ходе исследования зависимости частоты и амплитуды высвобождающегося Са²⁺ от скорости заполнения люмена и параметра взаимодействия между каналами построена 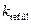– k фазовая диаграмма, совмещенная с графиками плотности, на которых выделены различные моды поведения системы в зависимости от параметров k и :

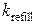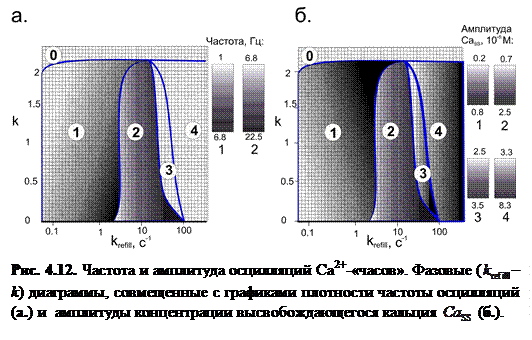
На рисунке справа от диаграмм представлены цветовые шкалы, отображающие значения частоты и амплитуды 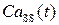в различных модах.

Мода 0: Статическое равновесие: при сильном взаимодействии между каналами происходит перенормировка ветвей конформационного потенциала в направлении стабильности закрытого состояния. Так, при k > 2.3 даже при максимальном заполнении люмена закрытое состояние остается стабильным, и в связи с этим не происходит туннелирования каналов в открытое состояние.

Мода 1: Релаксационные осцилляции. (рис. 4.11(1)). При достаточно малой скорости заполнения (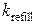 <10 с^-1) система ведет себя как устойчивый релаксационный осциллятор. После завершения высвобождения уровень 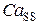понижается до нулевого уровня вследствие низкой частоты высвобождений. В данной моде частота осцилляций 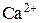варьируется в достаточно широком интервале (от 1 до 6.8 Гц), как показывает градация цвета от белого к черному на графике плотности. Также следует указать на увеличение амплитуды концентрации высвободившегося Са²⁺ (от 5·10^-7 до 1.5·10^-6 М), что видно из рис. 4.11(1).

Мода 2: Гармонические высокочастотные осцилляции. (рис. 4.11(2)). При увеличении скорости заполнения 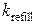увеличивается частота высвобождений, однако, уровень 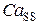не успевает понизиться до нулевого уровня. Как видно из рисунка, осцилляции системы носят гармонический характер.

Мода 3: Динамическое квазиравновесие. (рис. 4.11(3)). При дальнейшем увеличении скорости заполнения люмена (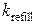 >50 с^-1) наблюдались осцилляции высокой частоты и достаточно малой амплитуды вблизи определенного значения концентрации ( 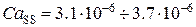M). Данные осцилляции вследствие малой амплитуды можно рассматривать как динамическое квазиравновесное состояние системы.

Мода 4: Динамическое равновесие. (рис. 4.11(4)). При большом значении параметра скорости заполнения (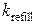 >200 с^-1) открывается весь кластер RyR-каналов. В этом случае наблюдается стабильное вытекание ионов 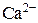в диадное пространство с постоянной скоростью.

На рисунке 4.13 представлены графики зависимосте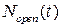й и 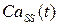в модах 1 и 2 при различных значениях .

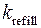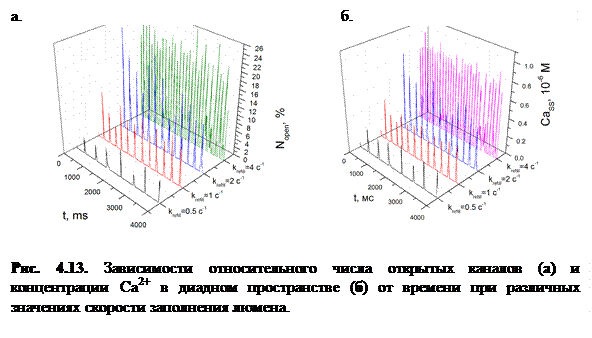
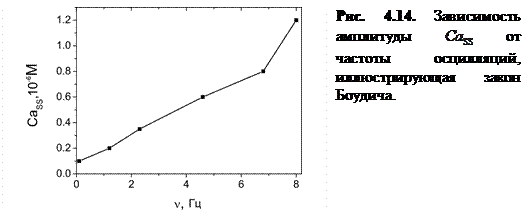
Как видно из рисунка, при увеличении 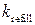происходит рост амплитуды концентрации высвободившегося Са²⁺. Следует отметить, что в модах 1 и 2 (оптимальный режим) наблюдается эффект увеличения амплитуды концентрации высвобождающегося 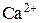с ростом частоты осцилляций (рис. 4.14). Одновременно с этим происходит увеличение амплитуды колебаний 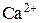в люмене и увеличение амплитуды осцилляций числа открытых каналов .

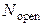Детальный анализ [А2] показал, что данный эффект может быть объяснен как результат задержки туннелирования каналов в открытое состояние. Это явление подробно описано ранее в пункте 4.1.3 настоящей работы. При большей скорости заполнения, как было показано, эффект задержки проявляется сильнее, чем при малой скорости заполнения люмена.

Данный эффект приводит к тому, что большей скорости заполнения соответствует больший уровень концентрации 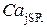, при котором достигаются оптимальные условия туннелирования между ветвями конформационного потенциала. В связи с этим в процессе высвобождения открывается бόльшее число каналов и высвобождается бόльшее количество ионов 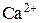в диадное пространство.

Если учесть прямую связь силы сокращений кардиомиоцитов с концентрацией высвободившегося 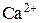[4, 70], то данный факт на молекулярном уровне объясняет давно известный принцип Боудича работы клеток водителей ритма «чаще-сильнее». Другими словами, внутренний СР-осциллятор в ЭК-модели может работать индивидуально как источник устойчивых сердечных сокращений.

Как уже отмечалось ранее, представления о динамике ионов Са²⁺ и о принципах работы внутренних Са²⁺-«часов» в данной работе основываются на модели Мальцева-Лакатты (ML) [87, 88]. Эта модель адекватно описывает кальциевую кинетику, но обладает рядом недостатков, в частности, пренебрежением кооперативной динамикой RyR-каналов в кластере высвобождающей единицы. Следует отметить, что ML-модель демонстрирует обратное «анти-Боудич» поведение 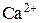-«часов» («выше частота, меньше амплитуда»), однако, эффект Боудича в этой модели воспроизводится только с учетом взаимодействия внутренних и мембранных 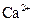-«часов» [89].

Автором данной диссертационной работы с помощью объединения модели кальциевой динамики с ЭК-моделью RyR-каналов впервые учтены кооперативные механизмы кинетики RyR-каналов и описан стохастический характер поведения этих каналов в процессе заполнения/высвобождения СР.

В отличие от ML-модели эффекты, связанные со стохастическим характером динамики каналов в модифицированной модели, позволяют объяснить причину увеличения амплитуды высвобождающегося Са²⁺ в диадное пространство с ростом частоты осцилляций изолированных внутренних Са²⁺-«часов», что в свою очередь позволяет на молекулярном уровне впервые описать эффект Боудича.

ЭК-модель также естественным образом вводит флуктуации частоты и амплитуды колебаний системы и шумы, нарушающие гармонический режим в модах 1 и 2. Следует отметить, что эти флуктуации заметно подавляются с ростом константы k конформационного взаимодействия между соседними RyR-каналами.

Date: 2015-08-24; view: 502; Нарушение авторских прав