Анализ кооперативной динамики RyR-каналов в кластере

При анализе модели особенно важным является изучение изменения динамики канала в зависимости от конформационного состояния его соседей при учете взаимодействия между каналами в кластере. В связи с этим была проведена серия численных экспериментов на квадратном кластере взаимодействующих RyR-каналов размерностью 9х9.

На рисунке 4.3а представлены графики конформационного потенциала RyR-канала, ближайшие соседи которого находятся в закрытом состоянии, при двух значениях параметра конформационного взаимодействия (k =0 и k =1). При сравнении этих графиков можно сделать вывод, что при включенном взаимодействии (пунктирная линия) закрытое состояние является более устойчивым, чем в случае при нулевом значении параметра k (без учёта взаимодействия) (сплошная линия).

На рисунке 4.3б представлены конформационные потенциалы канала с учетом взаимодействия с закрытыми соседями и без его учета при p =0.

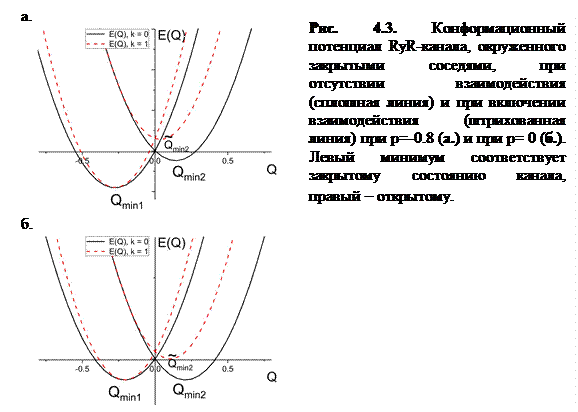
В отсутствие взаимодействия наблюдается равновесие локальных минимумов. В этом случае возможно туннелирование каналов из закрытого состояния в открытое. При включенном взаимодействии (штрихованная линия) закрытое состояние остается глобальным минимумом, и туннельный переход в открытое состояние запрещен.

При определенном значении параметра эффективного давления p устанавливается равновесие локальных минимумов КП. Условия, при которых возможно это равновесие, можно рассчитать аналитически.

Пусть канал находится в закрытом состоянии. Конформационная координата соседних каналов взаимодействующих с ним каналов равна минимуму при закрытом состоянии: 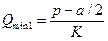. Две ветви конформационного потенциала (3.8) одиночного канала с учётом взаимодействия описываются формулами:

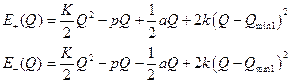. (4.1)

Подставляя значение , получим:

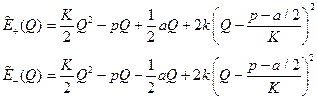. (4.2)

Далее можно найти положение минимумов конформационного потенциала с учетом взаимодействия: 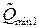и. 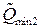(рис. 4.3). Приравнивая производную функций (3.13) по Q к нулю, получим систему уравнений:

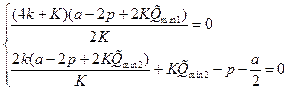, (4.3)

при решении которой находятся значения минимумов конформационного потенциала: , .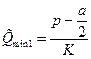

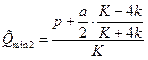Разность энергий минимумов открытого и закрытого состояний равна: 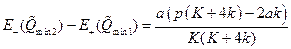. (4.4)

Приравняв к нулю (3.15) можно получить зависимость параметра p от параметра взаимодействия k, при котором наблюдается равновесие локальных минимумов КП:

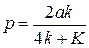(4.5).

График зависимостей p (k) и 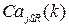представлен на рисунке 4.4.

Как видно из рисунка, с ростом параметра k увеличивается пороговое значение 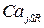. Это означает, что при сильном взаимодействии между каналами необходим более высокий уровень 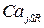, при котором начинается процесс открытия каналов, чем в случае слабого взаимодействия.

4.1.3 Эффект задержки туннелирования в процессе динамики Са²⁺

Для изучения процесса туннелирования каналов в открытое состояние при заполнении люмена ионами Са²⁺ была проведена серия численных экспериментов в рамках электронно-конформационной модели.

В начальный момент времени все каналы находились в закрытом состоянии, уровень 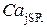равнялся 0.05 мМ, значение параметра эффективного давления: 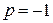. С течением времени происходило заполнение люмена с константой скорости заполнения 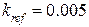мс^-1. Значение уровня концентрации 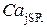, при котором параметр 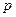достигает нулевого значения: 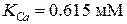. Взаимодействие между каналами не учитывалось.

На рисунке 4.5 приведены временные зависимости параметра р и относительного числа открытых каналов в кластере ().

Рис. 4.5.Зависимости значений параметра (пунктирная линия) и относительного числа открытых каналов в кластере (сплошная линия) от времени.

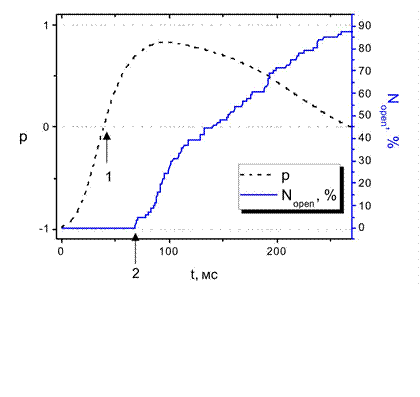
Как видно из рисунка, параметр 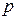достигает нулевого уровня в момент времени 39 мс (стрелка 1), однако каналы начинают открываться только в момент времени 67 мс с начала эксперимента (стрелка 2).

По представлениям модели в момент, когда 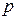достигает нулевого значения, минимум конформационного потенциала, соответствующий закрытому состоянию, становится метастабильным, и должно начинаться туннелирование каналов в открытое состояние. Однако в эксперименте наблюдалась задержка процесса туннелирования.

При анализе экспериментов было выявлено, что данную задержку открытия каналов определяют особенности конформационной динамики RyR-канала. Необходимо рассмотреть более подробно процесс изменения конформационного потенциала при заполнении люмена, схематично изображенный на рисунке 4.6.

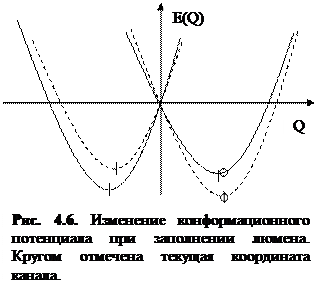
Процесс туннелирования может совершаться только если система находится в малой окрестности ε вблизи точки локального минимума. Пусть в момент времени t (пунктирная линия) конформационная координата канала Q соответствует локальному минимуму. В момент времени 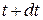(сплошная линия) координата будет той же, но вследствие увеличения параметра 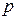при заполнении люмена минимум сдвинется вправо. Как видно из рисунка, канал будет находиться левее минимума, то есть вне зоны, где разрешены туннельные переходы. Другими словами, системе требуется время для медленной конформационной «подстройки» под новые условия, то есть под новую форму конформационного потенциала.

На рисунке 4.7 представлены временные зависимости параметра эффективного давления р и расстояния от конформационной координаты Q до минимума конформационного потенциала (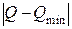). Зависимости приведены при различных значениях скорости заполнения люмена.

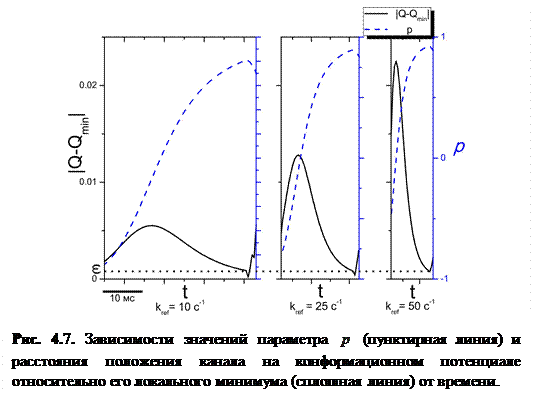
Как видно из рисунка сначала расстояние растет со временем до определенного момента, затем канал, «подстраиваясь» под новые условия стремится к новому минимуму, расстояние сокращается. Чем быстрее изменяется КП, тем больше максимальное расстояние до минимума.

Данный эффект определяет некоторую инерцию нашей системы при «подстраивании» под новые физические условия.

4.1.4 Анализ модели динамики ионов Са²⁺ между компартментами клетки

В представленной в диссертационной работе модели внутриклеточных Са²⁺-«часов» предполагается следующая схема динамики ионов Са²⁺:

· В начале цикла уровень 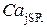достаточно мал, все каналы в кластере закрыты. Уровень 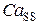является достаточно низким для электронной стимуляции каналов. Происходит заполнение люмена ионами, диффундирующими по градиенту концентрации из сети СР.

· При достижении критического уровня 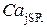= 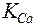закрытое состояние RyR-каналов становится метастабильным, начинается туннелирование некоторого числа каналов в открытое состояние, инициирующее высвобождение Са²⁺ в диадное пространство.

· Малое «первичное» спонтанное высвобождение 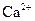из люмена в диадное пространство является своеобразным триггером, инициирующим дальнейшую электронную активацию RyR-каналов. Когда концентрация 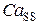достигает некоторого критического значения, она усиливает процесс «вторичного» высвобождения 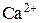посредством механизма КВВК.

· Достаточно сильное «вторичное» высвобождение 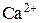в свою очередь резко уменьшает уровень 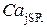, понижая тем самым стабильность открытого состояния каналов, что приводит к их дальнейшему закрытию.

· Высвобожденный 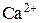диффундирует в цитозоль, а затем поглощается сетью СР (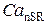). С понижением уровня 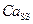вследствие диффузии в цитозоль уменьшается вероятность электронной активации каналов, что приводит к завершению «вторичного» высвобождения.

· Вследствие высвобождения Са²⁺ из СР минимум конформационного потенциала, соответствующий закрытому состоянию, становится глобальным. Происходит туннелирование открытых каналов в закрытое состояние, что приводит к прекращению высвобождения.

· В процессе заполнения люмена и достаточно медленного увеличения 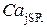происходит постепенное открытие RyR-каналов, затем имеет место следующее высвобождение и т.д.

Длительность задержки между высвобождениями определяется скоростью закачки 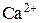из цитозоля в сеть СР (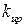), диффузии из сети СР в люмен (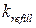), высвобождения из люмена в диадное пространство (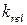) и диффузии из диадного пространства в цитозоль ().

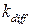Анализируя данную схему, можно провести параллель между моделью Са²⁺-«часов» и гидродинамической моделью типа «накопление-сброс» на примере сосуда, медленно заполняемого водой (рис. 4.8а). Эта модель подробно исследована в работе [124].

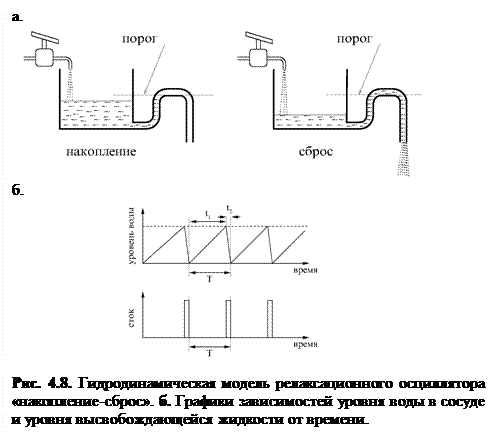
В модели «накопление-сброс» происходит заполнение резервуара водой с постоянной скоростью. Когда уровень жидкости достигает порогового уровня, сосуд быстро опорожняется через сифон, и начинается новый цикл его заполнения. Процесс опорожнения является повторяющимся, то есть при постоянной подкачке с определенной скоростью заполнения извне данная система может вести себя как релаксационный осциллятор с характерным периодом колебаний T (рис. 4.8б). Форма таких колебаний очень далека от синусоидальной; она скорее напоминает последовательность импульсов. На графике зависимости уровня воды в сосуде от времени хорошо видны два характерных интервала времени t ₁ и t ₂, связанных с медленным заполнением и быстрым опорожнением, соответственно.

Если представить процесс с достаточно быстрым заполнением резервуара или с достаточно медленным опорожнением (времена t ₁ и t ₂ – соизмеримы), то колебания уровня воды, стекающей через сифон, будут иметь гармонический характер. При скорости заполнения большей по значению скорости сброса уровень жидкости будет держаться выше порогового, и будет происходить постоянное высвобождение воды из резервуара.

Роль «порога» в модели Са²⁺-«часов» играют несколько факторов. Во-первых, критический уровень концентрации Са²⁺ в люмене, выше которого вероятность туннелирования RyR-каналов в открытое состояние становится ненулевой. Во-вторых, критическое значение концентрации Са²⁺ в диадном пространстве, выше которого начинаются электронные переходы каналов в открытое состояние, вследствие чего начинается вторичное высвобождение Са²⁺ из ретикулума.

С другой стороны, рассматривая электронные переходы, мы сделали предположение, что их вероятность является Са²⁺-зависимой. В ЭК-модели, интегрированной в модель ВЕ, эти вероятности будут зависеть от уровня 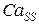, в чём и состоит процесс КВВК в нашей теории.

Рассмотрим один цикл работы Са²⁺-«часов» (рис. 1.20). В начальный момент времени каналы в кластере находятся в закрытом состоянии и уровень 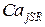лежит ниже значения 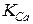, то есть 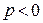. При заполнении люмена происходит перенормировка КП; в определенный момент времени значение 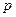достигает нулевого уровня. Вследствие этого закрытое состояние становится метастабильным, начинается туннелирование небольшого числа каналов в открытое состояние. Данный процесс получил называние первичное высвобождение, вследствие которого повышается уровень 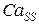. Данное повышение 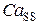увеличивает вероятность электронных переходов, что приводит к процессу открытия большего количества каналов. Происходит процесс вторичного (усиленного) высвобождения.

Высвобождение вызывает достаточно резкое понижение концентрации Са²⁺ в люмене, понижается значения 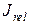, так оно зависит от разности концентраций 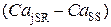. Понижается уровень 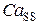, в связи с этим уменьшается вероятность электронной стимуляции каналов.

При понижении уровня 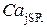ниже значения 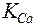начинается туннелирование каналов из открытого состояния в закрытое.

4.2 Результаты моделирования Са²⁺ высвобождающей единицы

В этом разделе диссертационной работы приведены основные результаты компьютерных экспериментов в рамках электронно-конформационной теории и модели высвобождающей единицы. Эти эксперименты проводились с целью изучения динамики ионов Са²⁺ в высвобождающей единице клеток водителей сердечного ритма.

В рамках рассматриваемой модели исследовано влияние таких факторов, как скорости перетекания ионов Са²⁺ между компартментами клетки и взаимодействие между каналами, на стабильность авторитмических колебаний внутренних Са²⁺-«часов».

Date: 2015-08-24; view: 647; Нарушение авторских прав