Однородные координаты и матрицы преобразований

Поскольку трёхмерная матрица поворота не несёт информации о поступательном перемещении и используемом масштабе, вектор координат р = (р _x, р_y, р_z) ^T в трёхмерном пространстве дополняют четвёртой координатой (или компонентой) так, что он принимает вид: 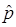= (wр_x, wр_y, wр_z, w) ^T. Тогда вектор выражен в однородных координатах.

Описание точек трёхмерного пространства однородными координатами позволяет ввести в рассмотрение матричные преобразования, содержащие одновременно поворот, параллельный перенос, изменение масштаба и преобразование перспективы.

В общем случае изображение N -мерного вектора размерностью N+1 называется представлением в однородных координатах. При таком представлении преобразование N -мерного вектора производится в (N+1)-мерном пространстве, а физический N -мерный вектор получается делением однородных координат на (N+1)-ю компоненту .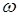

Так, вектор р = (р_x, р_y, р_z) ^T положения в трёхмерном пространстве в однородных координатах представляется расширенным вектором (wр_x, wр_y, wр_z, w) ^T.

Физические координаты связанны с однородными следующим образом:

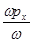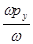р_x = , р_y= , р_z= ,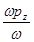

где w – четвёртая компонента вектора однородных координат (масштабирующий множитель).

Если w = 1, то однородные координаты вектора положения совпадают с его физическими координатами.

Однородная матрица преобразования представляет собой матрицу размерностью 4´4, которая преобразует вектор, выраженный в однородных координатах, из одной системы отсчёта в другую.

Однородная матрица преобразования может быть разбита на четыре подматрицы:

Т = = . (4-1)

Верхняя левая подматриа размерностью 3×3 представляет собой матрицу поворота; верхняя правая подматрица размерностью 3×1 представляет собой вектор положения начала координат повернутой системы отсчета относительно абсолютной; Нижняя левая подматрица размерностью 1×3 задает преобразование перспективы; четвертый диагональный элемент является глобальным масштабирующим множителем. Однородная матрица преобразования позволяет выявить геометрическую связь между связанной системой отсчёта OUVW и абсолютной системой OXYZ.

Если вектор р трехмерного пространства выражен в однородных координатах, т.е. , то, используя понятие матрицы преобразования можно сформировать однородную матрицу преобразования Т_пов, задающую преобразование поворота и имеющую размерность 4×4. Однородная матрица поворота получается соответствующим расширением обычной матрицы поворота, имеющей размерность 3×3. Так, однородное представление для матриц (2-12) и (2-13) имеет следующий вид:

, ,

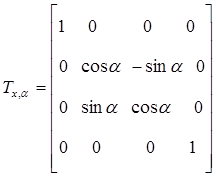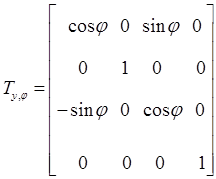. (4-2)

Эти матрицы размерностью 4×4 называются однородными матрицами элементарных поворотов. Однородная матрица преобразования переводит вектор, заданый однородными координатами в системе отсчета OUVW, в абсолютную систему координат OXYZ, т.е. при :

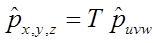(4-3)

и . (4-4)

Date: 2015-08-15; view: 634; Нарушение авторских прав