
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Задача Д1
|
|
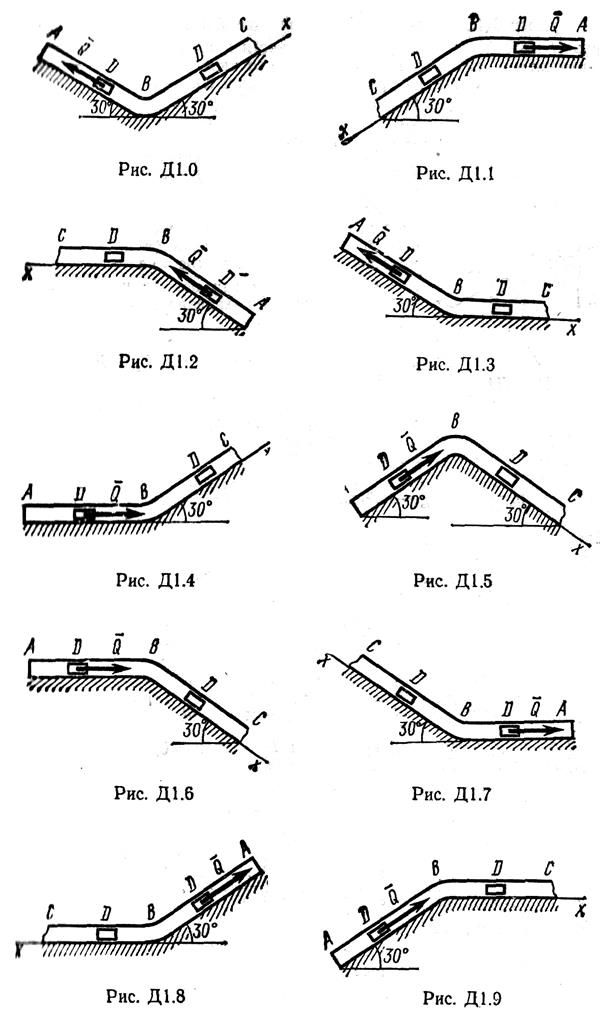
Груз D массой m, получив в точке А начальную скорость υ0, движется в изогнутой трубе ABC, расположенной в вертикальной плоскости; участки трубы или оба наклонные, или один горизонтальный, а другой наклонный (рис. Д1.0 – Д1.9, табл. Д1). На участке АВ, на груз кроме силы тяжести, действуют постоянная сила 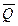 (ее направление показано на рисунках) и сила сопротивления среды
(ее направление показано на рисунках) и сила сопротивления среды 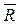 , зависящая от скорости
, зависящая от скорости 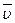 груза (направлена против движения); трением груза о трубу на участке АВ пренебречь.
груза (направлена против движения); трением груза о трубу на участке АВ пренебречь.
В точке В груз, не изменяя своей скорости, переходит на участок ВС трубы, где на него, кроме силы тяжести, действуют сила трения (коэффициент трения груза о трубу f = 0,2) и переменная сила 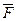 , проекция которой F x на ось х задана в таблице. Считая груз материальной точкой и зная расстояние АВ = l или время t1 движения груза от точки А до точки В, найти закон движения груза на участке ВС, т. е. x = f(t), где x = BD.
, проекция которой F x на ось х задана в таблице. Считая груз материальной точкой и зная расстояние АВ = l или время t1 движения груза от точки А до точки В, найти закон движения груза на участке ВС, т. е. x = f(t), где x = BD.
Указания. Задача Д1 – на интегрирование дифференциальных уравнений движения точки. (Решение основной задачи механики). Решение задачи разбивается на две части. Сначала нужно составить и проинтегрировать методом разделения переменных дифференциальное уравнение движения точки (груза) на участке AB, учтя начальные условия. Затем, зная время движения груза на участке АВ или длину этого участка, определить скорость груза в точке В. Эта скорость будет начальной для движения груза на участке ВС. После этого нужно составить и проинтегрировать дифференциальное уравнение движения груза на участке ВС тоже с учетом начальных условий, ведя отсчет времени от момента, когда груз находится в точке В, и полагая в этот момент t=0. При интегрировании уравнения движения на участке АВ в случае, когда задана длина l участка, целесообразно перейти к переменной х, учтя, что: 
Таблица Д1
| Номер условия | m, кг | υ0, м/с | Q, H | R, H | l, м | t, c | Fx, H |
| 0,4υ | - | 2,5 | 2sin(4t) | ||||
| 2,4 | 0,8 υ2 | 1,5 | - | 6t | |||
| 4,5 | 0,5 υ | - | 3sin(2t) | ||||
| 0,6 υ2 | - | -3cos(2t) | |||||
| 1,6 | 0,4 υ | - | 4cos(4t) | ||||
| 0,5 υ2 | - | -6sin(2t) | |||||
| 1,8 | 0,3 υ | - | 9t2 | ||||
| 0,8 υ2 | 2,5 | - | -8cos(4t) | ||||
| 0,5 υ | - | 2cos(2t) | |||||
| 4,8 | 0,2 υ2 | - | -6sin(4t) |
Пример Д1. На вертикальном участке АВ трубы (рис. Д1) на груз D массой m действует сила тяжести и сила сопротивления 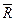 ; движение от точки А, где υ0=0, до точки В длится t1 c. На наклонном участке ВС на груз действуют сила трения (коэффициент трения груза о трубу равен f) и переменная сила F=F(t), заданная в ньютонах.
; движение от точки А, где υ0=0, до точки В длится t1 c. На наклонном участке ВС на груз действуют сила трения (коэффициент трения груза о трубу равен f) и переменная сила F=F(t), заданная в ньютонах.
 Дано: m=8кг, R=μυ2, где μ=0,2 кг/м, υ0=0, t1=2c, f=0.2, Fx=16 sin (4t), α=30˚.
Дано: m=8кг, R=μυ2, где μ=0,2 кг/м, υ0=0, t1=2c, f=0.2, Fx=16 sin (4t), α=30˚.
Определить: x=f(t) – закон движения груза на участке ВС.
Решение. 1. Рассмотрим движение груза на участке АВ, считая груз материальной точкой. Изображаем груз (в произвольном положении) и действующие на него силы  . Проводим ось Аz и составляем дифференциальное уравнение движения груза в проекции на эту ось:
. Проводим ось Аz и составляем дифференциальное уравнение движения груза в проекции на эту ось:
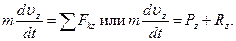 (1)
(1)
Далее находим Pz=P=mg, Rz=-R=-μυ2; подчеркиваем, что в уравнении все переменные силы надо обязательно выразить через величины, от которых они зависят. Учтя еще, что υz=υ, получим
 (2)
(2)
Введем для сокращения записей обозначение
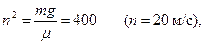 (3)
(3)
где при подсчете принято g≈ 10 м/с2. Тогда, разделяя в уравнении (2) переменные и взяв затем от обеих частей равенства интегралы, получим
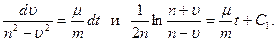 (4)
(4)
По начальным условиям при t = 0 υ=υ0=0, что дает С1=(1/2n)×ln 1 =0. Введя еще одно обозначение
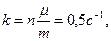 (5)
(5)
получим из (4)

Отсюда находим, что
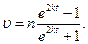 (6)
(6)
Полагая здесь t=t1=2 c и заменяя n и k их значениями (3) и (5), определим скорость υВ груза в точке В (число е=2,7):
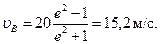 (7)
(7)
2. Рассмотрим движение груза на участке ВС; найденная скорость υВ будет для движения на этом участке начальной скоростью (υ0= υВ). Изображаем груз (в произвольном положении) и действующие на него силы 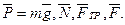 Проведем из точки В оси Вх и Ву и составим дифференциальное уравнение движения груза в проекции на ось Вх:
Проведем из точки В оси Вх и Ву и составим дифференциальное уравнение движения груза в проекции на ось Вх:
 или
или
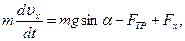 (8)
(8)
где FТР=fN. Для определения N составим уравнение в проекции на ось Вy. Так как ау=0, получим 0=N-mgcosα, откуда N=mgcosα. Следовательно, Fтр=fmgcosα; кроме того, Fx=16sin(4t) и управление (8) примет вид
 (9)
(9)
Разделив обе части равенства на m, вычислим
g(sinα – f cos α)=g(sin30˚-0,2cos30˚)=3,2; 16/m=2 и поставим эти значения в (9). Тогда получим
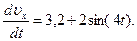 (10)
(10)
Умножая обе части уравнения (10) на dt и интегрируя, найдем
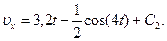 (11)
(11)
Будем теперь отсчитывать время от момента, когда груз находится в точке В, считая в этот момент t=0. Тогда при t=0 υ=υ0=υВ, где υВ дается равенством (7). Подставляя эти величины в (11), получим
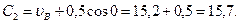
При найденном значении С2 уравнение (11) дает
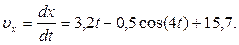 (12)
(12)
Умножая здесь обе части на dt и снова интегрируя, найдем
x=1,6t2-0.13sin(4t)+15,7t+C3. (13)
Так как при t=0 x=0, то C3=0 и окончательно искомый закон движения груза будет
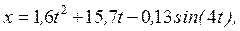 (14)
(14)
где x – в метрах, t – в секундах.
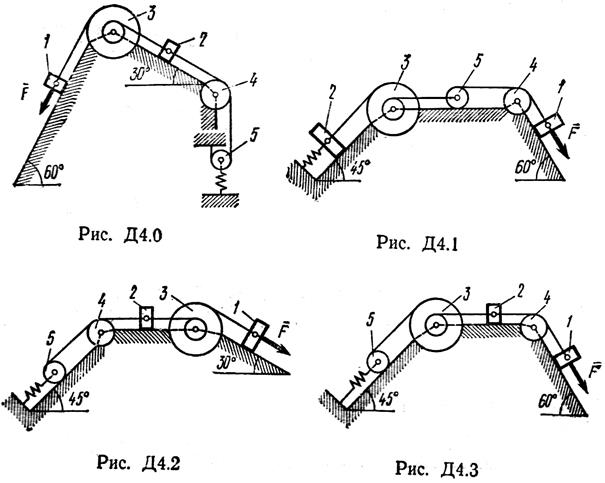
Задача Д4
Механическая система состоит из грузов 1 и 2, ступенчатого шкива 3 с радиусами ступеней R3 = 0,3 м, r3 = 0,1 м и радиусом инерции относительно оси вращения ρ3 = 0,2м, блока 4 радиуса R4 = 0,2 м и катка (или подвижного блока) 5 (рис. Д4.0 – Д4.9, табл. Д4); тело 5 считать сплошным однородным цилиндром, а массу блока 4 – равномерно распределенной по ободу. Коэффициент трения грузов о плоскость f = 0,1. Тела системы соединены друг с другом нитями, перекинутыми через блоки и намотанными на шкив 3 (или на шкив и каток); участки нитей параллельны соответствующим плоскостям. К одному из тел прикреплена пружина с коэффициентом жесткости с.
Под действием силы F = f(s), зависящей от перемещения s точки ее приложения, система приходит в движение из состояния покоя; деформация пружины в момент начала движения равна нулю. При движении на шкив 3 действует постоянный момент М сил сопротивления (от трения в подшипниках).
Определить значение искомой величины в тот момент времени, когда перемещение s станет равным s1 = 0,2 м. Искомая величина указана в столбце «Найти» таблицы, где обозначено: υ1, υ2, υс5 – скорости грузов 1, 2 и центра масс тела 5 соответственно, ω3 и ω4 – угловые скорости тел 3 и 4.
Все катки, включая и катки, обмотанные нитями (как, например, каток 5 на рис. 1), катятся по плоскостям без скольжения.
На всех рисунках не изображать груз 2, если m2=0; остальные тела должны изображаться и тогда, когда их масса равна нулю.
Указания. Задача Д4 – на применение теоремы об изменении кинетической энергии системы. При решении задачи учесть, что кинетическая энергия Т системы равна сумме кинетических энергий всех входящих в систему тел; эту энергию нужно выразить через ту скорость (линейную или угловую), которую в задаче надо определить. При вычислении Т для установления зависимости между скоростями точек тела, движущегося плоскопараллельно, или между его угловой скоростью и скоростью центра масс воспользоваться мгновенным центром скоростей (кинематика). При вычислении работы надо все перемещения выразить через заданное перемещение s1, учтя, что зависимость между перемещениями здесь будет такой же, как между соответствующими скоростями.
Таблица Д4
| Номер условия | m1, кг | m2, кг | m3, кг | m4, кг | m5, кг | с, Н/м | М, Н×м | F=f(s), H | Найти |
| 1,2 | 80(4+5s) | ω3 | |||||||
| 0,8 | 50(8+3s) | υ1 | |||||||
| 1,4 | 60(6+5s) | υ2 | |||||||
| 1,8 | 80(5+6s) | ω4 | |||||||
| 1,2 | 40(9+4s) | υ1 | |||||||
| 1,6 | 50(7+8s) | υС5 | |||||||
| 0,8 | 40(8+9s) | ω3 | |||||||
| 1,5 | 60(8+5s) | υ2 | |||||||
| 1,4 | 50(9+2s) | ω4 | |||||||
| 1,6 | 80(6+7s) | υС5 |
Пример Д4. Механическая система (рис. Д4, а) состоит из сплошного однородного цилиндрического катка 1, подвижного блока 2, ступенчатого шкива 3 с радиусами ступеней R3 и r3 и радиусом инерции относительно оси вращения ρ3, блока 4 и груза 5(коэффициент трения груза о плоскость равен f). Тела системы соединены нитями, намотанными на шкив 3. К центру Е блока 2 прикреплена пружина с коэффициентом жесткости с; ее начальная деформация равна нулю. Система приходит в движение из состояния покоя под действием силы F=f(s), зависящей от перемещения s точки ее приложения. На шкив 3 при движении действует постоянный момент М сил сопротивления.
Дано: m1 = 8 кг, m2 = 0, m3 = 4 кг, m4 = 0, m5 =10 кг, R3 = 0,3 м, r3 = 0,1 м,
ρ3 = 0,2 м, f=0,1, c=240 Н/м, M=0,6 Н×м, F=20(3+2s)Н, s1=0,2 м.
Определить ω3 в тот момент времени, когда s=s1.
Решение. 1. Рассмотрим движение неизменяемой механической системы, состоящей из весомых тел 1, 3, 5 и невесомых тел 2, 4, соединенных нитями. Изобразим действующие на систему внешние силы: активные 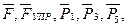 реакции
реакции 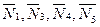 , натяжение нити
, натяжение нити 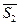 , силы трения
, силы трения 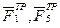 и момент М.
и момент М.
Для определения ω3 воспользуемся теоремой об изменении кинетической энергии:
 (1)
(1)
2. Определяем Т0 и Т. Так как в начальный момент система находилась в покое, то Т0=0. Величина Т равна сумме энергий всех тел системы:
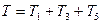 . (2)
. (2)
Учитывая, что тело 1 движется плоскопараллельно, тело 5 – поступательно, а тело 3 вращается вокруг неподвижной оси, получим
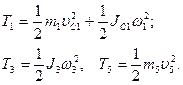 (3)
(3)
Все входящие сюда скорости надо выразить через искомую ω3. Для этого предварительно заметим, что υС1=υ5=υА, где А – любая точка обода радиуса r3 и что точка К1 – мгновенный центр скоростей катка 1, радиус которого обозначим r1. Тогда
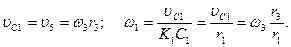 (4)
(4)
Кроме того, входящие в (3) моменты инерции имеют значения
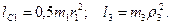 (5)
(5)
Подставив все величины (4) и (5) в равенства (3), а затем, используя равенство (2), получим окончательно
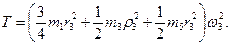 (6)
(6)
3. Теперь найдем сумму работ всех действующих внешних сил при том перемещении, которое будет иметь система, когда точка С1 пройдет путь s1. Введя обозначения: s5 – перемещение груза 5 (s5=s1), φ3 – угол поворота шкива 3, λ0 и λ1 – начальное и конечное удлинения пружины, получим
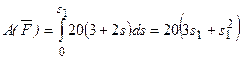 ;
;
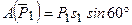 ;
;

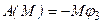 ;
; 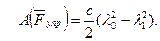
Работы остальных сил равны нулю, так как точки К1 и К2, где приложены силы 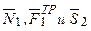 - мгновенные центры скоростей; точки, где приложены
- мгновенные центры скоростей; точки, где приложены 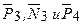 - неподвижны; а реакция
- неподвижны; а реакция  перпендикулярна перемещению груза.
перпендикулярна перемещению груза.
По условиям задачи λ0=0. Тогда λ1=sЕ, где sЕ – перемещение точки Е (конца пружины). Величины sE и φ3 надо выразить через заданное перемещение s1; для этого учтем, что зависимость между перемещениями здесь такая же, как и между соответствующими скоростями. Тогда, поскольку ω3=υА/r3=υC1 /r3 (равенство υС1=υА уже отмечалось), то и φ3=s1/r3.
Далее, из рисунка Д4, б видно, что υD=υB=ω3R3, а так как точка К2 является мгновенным центром скоростей для блока 2 (он как бы «катится по участку нити K2L), то υЕ=0,5υD=0,5ω3R3, следовательно, и λ1=sE=0,5φ3R3=0,5s1R3/r3. При найденных значениях φ3 и λ1 для суммы всех вычисленных работ получим
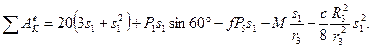 (7)
(7)
Подставляя выражения (6) и (7) в уравнение (1) и учитывая, что Т0=0, придем к равенству
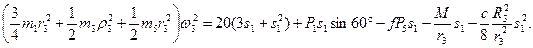 (8)
(8)
Из равенства (8), подставив в него числовые значения заданных величин, найдем искомую угловую скорость ω3. Ответ: ω3=8,1с-1.

Рис.Д4


Задача Д9
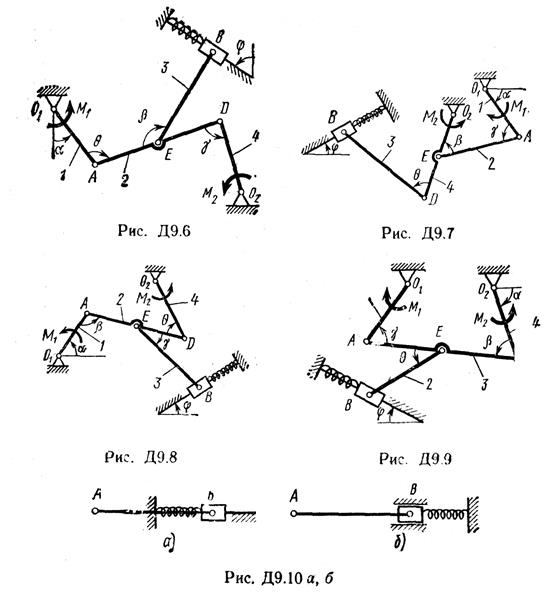
Механизм, расположенный в горизонтальной плоскости, находится под действием приложенных сил в равновесии; положение равновесия определяется углами a, b, g, j, q (рис. Д9.0 – Д9.9, табл. Д9а и Д9б). Длины стержней механизма (кривошипов) равны: l 1 = 0,4 м, l 4 = 0,6 м (размеры l 2 и l 3 произвольны); точка Е находится в середине соответствующего стержня.
На ползун В механизма действует сила упругости пружины 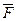 ; численно F = сl, где с — коэффициент жесткости пружины, l — ее деформация. Кроме того, на рис. Д9.0 и Д9.1 на ползун D действует сила
; численно F = сl, где с — коэффициент жесткости пружины, l — ее деформация. Кроме того, на рис. Д9.0 и Д9.1 на ползун D действует сила  , а на кривошип 01А — пара сил с моментом М; на рис. Д9.2—Д9.9 на кривошипы 01А и 02D действуют пары сил с моментами М1 и М2.
, а на кривошип 01А — пара сил с моментом М; на рис. Д9.2—Д9.9 на кривошипы 01А и 02D действуют пары сил с моментами М1 и М2.
Определить, чему равна при равновесии деформация l пружины, и указать, растянута пружина или сжата. Значения всех заданных величин приведены в табл. Д9а для рис. Д9.0—Д9.4 и в табл. Д9б для рис. Д9.5—Д9.9, где Q выражено в ньютонах, а М, М1, М2 — в ньютон-метрах.
Построение чертежа начинать со стержня, направление которого определяется углом α; для большей наглядности ползун с направляющими и пружину изобразить так, как в примере Д9 (см. рис. Д9, а также рис. Д9.10б). Если на чертеже решаемого варианта задачи прикрепленный к ползуну В стержень окажется совмещенным с пружиной (как на рис. Д9.10а), то пружину следует считать прикрепленной к ползуну с другой стороны (как на рис. Д9.10б, где одновременно иначе изображены направляющие).
Указания. Задача Д9 — на определение условий равновесия механической системы с помощью принципа возможных перемещений. Механизм в рассматриваемой задаче имеет одну степень свободы, т. е. одно независимое возможное перемещение. Для решения задачи нужно сообщить механизму возможное перемещение, вычислить сумму элементарных работ всех действующих активных сил и пар на этом перемещении и приравнять ее к нулю. Все вошедшие в составленное уравнение возможные перемещения следует выразить через какое-нибудь одно.
Чтобы найти l, надо из полученного условия равновесия определить силу упругости F. На чертеже эту силу можно направить в любую сторону
(т. е. считать пружину или растянутой или сжатой); верно ли выбрано направление силы, укажет знак.
Таблица Д9а (к рис. Д9.0—Д9.4)
| Номер условия | Углы, град | с, Н/см | Для рис. 0—1 | Для рис.2 - 4 | ||||||
| α | β | g | j | q | М, Н∙м | Q, Н | М1, Н∙м | M2, Н∙м | ||
Таблица Д9б (к рис. Д9.5—Д9.9)
| Номер условия | Углы, град | с, Н/см | М1, Н∙м | M2, Н∙м | ||||
| α | β | g | j | q | ||||
Пример Д9. Механизм (рис. Д9а), расположенный в горизонтальной плоскости, состоит из стержней 1, 2, 3 и ползунов B, D, соединенных друг с другом и с неподвижной опорой О1 шарнирами.
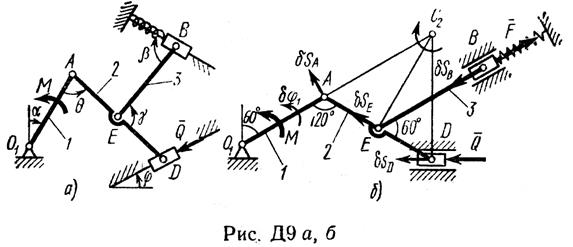
К ползуну В прикреплена пружина с коэффициентом жёсткости с, к ползуну D приложена сила  , а к стержню 1 (кривошипу) — пара сил с моментом М.
, а к стержню 1 (кривошипу) — пара сил с моментом М.
Дано: α = 60 °, β = 0 °, γ= 60 °, φ = 0 °, θ = 120 °, l = 0,4 м, АЕ = ЕD,
с= 125 Н/см, М = 150 Н×м, Q = 350 Н.
О п р е д е л и т ь: деформацию λ пружины при равновесии механизма.
Решение. 1. Строим положение механизма в соответствии с заданными углами (рис. Д9б); при этом согласно последнему из указаний к задаче Д9 прикрепляем пружину к ползуну с другой стороны (так, как если бы было β = 180°).
Для решения задачи воспользуемся принципом возможных перемещений, согласно которому
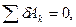 (1)
(1)
где δAk — элементарные работы активных сил на соответствующих возможных перемещениях.
Изображаем действующие на механизм активные силы: силу  , силу упругости
, силу упругости 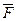 пружины (предполагая, что пружина растянута) и пару сил с моментом М.
пружины (предполагая, что пружина растянута) и пару сил с моментом М.
Неизвестную силу F найдем с помощью уравнения (1), а зная F и учитывая, что F = cλ, определим λ.
2. Чтобы составить уравнение (1), сообщим механизму возможное перемещение и введем следующие обозначения для перемещений звеньев, к которым приложены активные силы: δφ1 — поворот стержня 1 вокруг оси О1, δsD и δsB — перемещения ползунов (точек) D и В.
Из перемещений δφ1, δsD, δsB независимое от других — одно (у механизма одна степень свободы). Примем за независимое возможное перемещение δφ1 и установим, какими тогда будут δsD и δsB, выразив их через δφ1; при этом важно верно определить и направления δsD, δsB, так как иначе в уравнении (1) будут ошибки в знаках.
При расчетах учтем, что зависимость между возможными перемещениями здесь такая же, как между соответствующими скоростями звеньев механизма при его движении и воспользуемся известными из кинематики соотношениями (ход расчетов такой же, как в примере КЗ).
Сначала найдем и изобразим δsA (направление δsA определяется направлением δφ1); получим

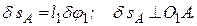 (2)
(2)
Теперь определим и изобразим δsD, учитывая, что проекции δsD и δsA на прямую АD должны быть равны друг другу (иметь одинаковые модули и знаки). Тогда
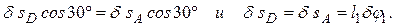 (3)
(3)
Чтобы определить δsB, найдем сначала δsE. Для этого построим мгновенный центр вращения (скоростей) С2 стержня 2 (на пересечении перпендикуляров к δsA и δsD, восстановленных из точек А и D) и покажем направление поворота стержня 2 вокруг С2, учтя направление δsA или δsD. Так как ÐС2АD = ÐC2DА = 60°, то DАС2D равносторонний и С2Е в нем высота, поскольку АЕ = ЕD. Тогда перемещение δsE, перпендикулярное С2Е, будет направлено по прямой ЕА (при изображении δsE учитываем направление поворота вокруг центра С2).
Воспользовавшись тем, что проекции δsE и δsA на прямую ЕА должны быть равны друг другу, получим (значение δsE можно найти и составив соответствующую пропорцию)
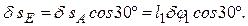 (4)
(4)
Наконец, из условия равенства проекций δsB и δsE на прямую ВЕ находим и изображаем δsB. Численно
δsB = δsE соs 60° = l1 δφ1соs 30° • соs60° = 0,43l1 δφ1. (5)
3. Теперь составляем для механизма уравнение (1); получим
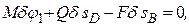 (6)
(6)
или, заменяя здесь δsD и δsB их значениями (3) и (5) и вынося одновременно δφ1 за скобки,
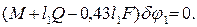 (7)
(7)
Так как δφ1¹0, то отсюда следует, что
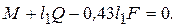 (8)
(8)
Из уравнения (8) находим значение F и определяем λ = F/с. Ответ: λ= 13,5 см. Знак указывает, что пружина, как и предполагалось, растянута. 

Задача Д10
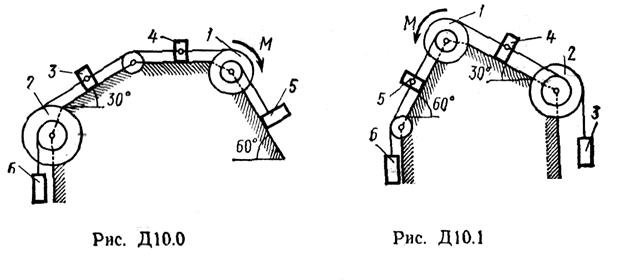
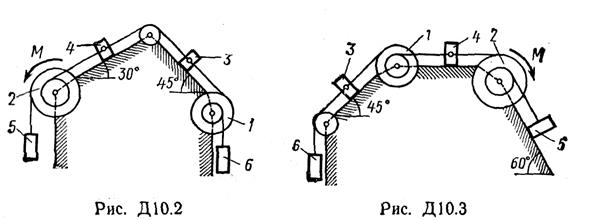
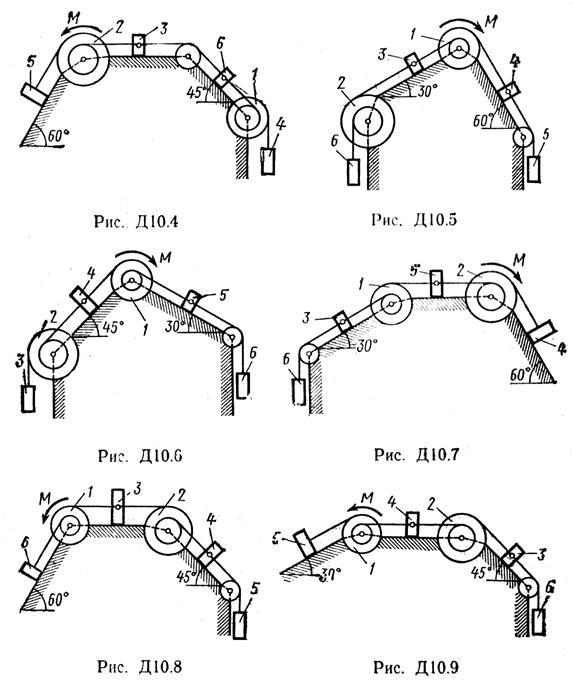
Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3—6, прикрепленных к этим нитям, и невесомого блока (рис. Д10.0—Д10.9, табл. Д10). Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М, приложенной к одному из шкивов. Радиусы ступеней шкива 1 равны:
R1 = 0,2 м, r1 = 0,1 м, а шкива 2 - R2 = 0,3 м, r2 = 0,15 м; их радиусы инерции относительно осей вращения равны соответственно ρ1=0,1 м и ρ2=0,2 м. Пренебрегая трением, определить ускорение груза, имеющего больший вес; веса Р1,..., Р6 шкивов и грузов заданы в таблице в ньютонах. Грузы, веса которых равны нулю, на чертеже не изображать (шкивы 1, 2 изображать всегда как части системы).
Указания. Задача Д10 – на применение (к изучению движения системы) общего уравнения динамики (принципа Даламбера – Лагранжа). Ход решения задачи такой же, как в задаче Д9, только предварительно надо присоединить к действующим на систему силам соответствующие силы инерции. Учесть при этом, что для однородного тела, вращающегося вокруг своей оси симметрии (шкива), система сил инерции приводится к паре с моментом М и = Jzε, где Jz – момент инерции тела относительно оси вращения, ε – угловое ускорение тела; направление М и противоположно направлению ε.
Таблица Д10
| Номер условия | P1 | P2 | P3 | P4 | P5 | P6 | M, H×м |
| 0,9 | |||||||
| 1,2 | |||||||
| 0,6 | |||||||
| 1,8 | |||||||
| 1,2 | |||||||
| 0,9 | |||||||
| 1,8 | |||||||
| 0,6 | |||||||
| 0,9 | |||||||
| 1,2 |
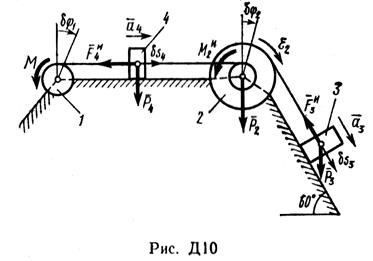 ПримерД10. Механическая система (рис. Д10) состоит из обмотанных нитями блока 1 радиуса R1 и ступенчатого шкива 2 (радиусы ступеней R2 и r2, радиус инерции относительно оси вращения ρ2), а также из грузов 3 и 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М, приложенной к блоку 1.
ПримерД10. Механическая система (рис. Д10) состоит из обмотанных нитями блока 1 радиуса R1 и ступенчатого шкива 2 (радиусы ступеней R2 и r2, радиус инерции относительно оси вращения ρ2), а также из грузов 3 и 4, прикрепленных к этим нитям. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом М, приложенной к блоку 1.
Дано: P1=0, P2 = 30 H, P3 = 40 H, P4 = 20 H, M = 16 H×м, R1 = 0,2 м, R2 = 0,3 м, r2 = 0,15 м, ρ2 = 0,2 м.
Определить ускорение груза 3, пренебрегая трением.
Решение. 1. Рассмотрим движение механической системы, состоящей из тел 1, 2, 3, 4, соединенных нитями. Система имеет одну степень свободы. Связи, наложенные на эту систему, - идеальные.
Для определения а3 применим общее уравнение динамики:
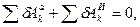 (1)
(1)
где 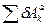 - сумма элементарных работ активных сил;
- сумма элементарных работ активных сил; 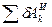 - сумма элементарных работ сил инерции.
- сумма элементарных работ сил инерции.
2. Изображаем на чертеже активные силы 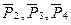 , и пару сил с моментом М. Задавшись, направлением ускорения
, и пару сил с моментом М. Задавшись, направлением ускорения 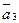 , изображаем на чертеже силы инерции
, изображаем на чертеже силы инерции  и пару сил инерции с моментом
и пару сил инерции с моментом 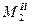 , величины которых равны:
, величины которых равны:
 (2)
(2)
3. Сообщая системе возможное перемещение и составляя уравнение (1), получим
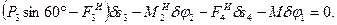 (3)
(3)
Выразим все перемещения через 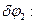
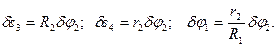 (4)
(4)
Подставив величины (2) и (4) в уравнение (3), приведем его к виду
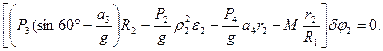 (5)
(5)
Входящие сюда величины ε2 и а4 выразим через искомую величину а3:
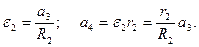
Затем, учтя, что δφ2¹0, принимаем равным нулю выражение, стоящее в (5) в квадратных скобках.
Из полученного в результате уравнения найдем

Вычисления дают следующий о т в е т: а 3 = - 0,9 м/с2. Знак указывает, что ускорения груза 3 и других тел направлены противоположно показанным на рис. Д10.
Список рекомендуемых источников
Основная литература
1. Бать М.И., Теоретическая механика в примерах и задачах./ М.И. Бать, Г.Ю. Джапаридзе, А.С. Кельзон. - Т. 1, 2. — М., 1964 [и последующие издания].
2. Кепе О.Э. Сборник коротких задач по теоретической механике/ О.Е. Кепе. — М.: Высшая школа, 1989.
3. Мещерский, И.В. Сборник задач по теоретической механике: учебное пособие/ И.В. Мещерский. — М., 1986 [и последующие издания].
4. Тарг С.М. Краткий курс теоретической механики: учебник/С.М. Тарг. — М., 1994.
5. Яблонский, А.А., Никифорова, В.М. Курс теоретической механики/А.А. Яблонский, В.М. Никифорова.— Ч. 1. — М.: Высшая школа, 1971 [и последующие издания].
Дополнительная литература
6. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Курс теоретической механики/ Н.В. Бутенин, Я.Л. Лунц, Д.Р. Меркин — Ч.1,2. — М.: Наука, 1971 [и последующие издания].
7. Бухгольц Н.Н. Основной курс теоретической механики/Н.М. Бухгольц. — Ч. 1. — М.: Наука, 1965.
8. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики/ Л.Г. Лойцянский, А.И. Лурье. — Ч.1,2. — М.-Л.: Физматгиз, 1952.
9. Никитин Н.Н. Курс теоретической механики: учебник/ Никитин Н.Н.— М.: Наука, 1990.
10. Сборник заданий для курсовых работ по теоретической механике: учебное пособие / под ред. А.А. Яблонского. — М.: Наука, 1998.
Date: 2015-08-15; view: 2069; Нарушение авторских прав