Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Теорема об изменении момента количества движения системы
|
|
Моментом количества движения системы точек относительно центра О называется вектор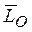 
, равный геометрической сумме векторов моментов количества движения всех точек системы относительно того же центра:
.
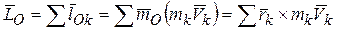Теорема: Производная по времени от момента количества движения системы точек относительно центра О равна сумме моментов внешних сил, действующих на точки системы относительно того же центра.
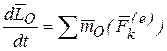(44)
Доказательство. Запишем теорему об изменении момента количества движения для точки с номером k: 
.
Записывая подобные уравнения для каждой точки системы, и суммируя их, получим: 
.
Учитывая, что по свойствам внутренних сил 
, получим, поменяв местами знаки суммирования и дифференцирования в левой части уравнения: 
, или 
. Что и требовалось доказать.
Теорема об изменении момента количества движения точки векторная, поэтому её можно записать в проекциях на оси координат:
; 
; 
.
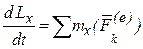Закон сохранения: Если в течение некоторого времени сумма моментов внешних сил, действующих на точки системы, относительно центра О равна нулю, то момент количества движения системы относительно этого центра все это время остается неизменным.
Date: 2015-08-15; view: 319; Нарушение авторских прав