Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Принцип Даламбера для точки и системы
|
|
Полученные ранее теоремы выведены из основного уравнения динамики. Те же теоремы можно получить и исходя из других положений, которые называются принципами механики.
Принцип Даламбера для точки формулируется так: если к активным силам и силам реакций связей, действующим на точку добавить силу инерции, то такая система сил будет уравновешенной:
. (50)
Здесь обозначено: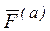 
– равнодействующая активных (заданных) сил, действующих на точку; 
– равнодействующая сил реакций; 
- сила инерции. Нетрудно увидеть, что принцип Даламбера для точки эквивалентен основному уравнению динамики (1). Действительно, подставив в (50) выражение для силы инерции, получим
,
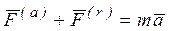что эквивалентно (1).
Применяя принцип Даламбера для каждой точки системы, получим
, k = 1…n. (51)
Здесь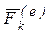 
, 
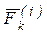– соответственно равнодействующие внешних и внутренних сил, действующих на точку с номером k, 
- сила инерции точки с номером k. Принцип Даламбера для системы (51) представляет собой n уравнений и формулируется так:
Date: 2015-08-15; view: 358; Нарушение авторских прав