Стійкість руху

Стійкість руху - поняття, яке характеризує тривале (довгочасне) зберігання будь-яких характеристик руху системи. Проблема стійкості руху виникає при вивченні гіроскопічних систем, систем автоматичного регулювання (наприклад, слідкуючих систем), коливних рухів, при дослідженні рухів літаків, ракет і т. д.. Ж.- Л. Лагранж вважав, що механічна система знаходиться в рівновазі, якщо під час руху відстані між її точками залишаються скінченними. Відомі визначення стійкості руху, які давали С.- Д. Пуассон, П.- С. Лаплас, М. Є. Жуковський та ін. Найбільш загальним і важливим за своїм застосуванням є визначення, яке дав стійкості руху О. М. Ляпунов. Рух будь-якої механічної системи можна обчислити теоретично, знаючи діючі на неї сили і початкові умови. Рух, який система згідно цих обчислень повинна здійснювати по Ляпунову, називається незбуреним рухом. Але практично система зазнає випадкових впливів, які не були враховані при обчисленнях. Якими б малими і короткочасними не були б ці впливи, вони приведуть до того, що в деякий момент t=t ₀ координати і швидкості точок системи одержать малі, але нерівні нулю прирости, які Ляпунов називає початковими збуреннями. Подальший рух називається збуреним рухом. Якщо при малих збуреннях деякі з характеристик руху в збуреному русі мало відрізняються від тих значень, які були в незбуреному русі, то по Ляпунову незбурений рух є стійким по відношенню до цих характеристик руху. Якщо при малих діях (збуреннях) значення розглядуваної характеристики буде в збуреному русі з часом все більше відхилятись від її значення в незбуреному русі, то незбурений рух є по відношенню до даної характеристики нестійким. Умови, при яких розглядуваний рух є стійким, називаються умовами (критеріями) стійкості.

В якості прикладу розглянемо рух симетричного вертикального гіроскопа (рис. 19.1).

Теоретично його вісь повинна залишатись вертикальною при будь-якій кутовій швидкості 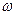. Однак фактично, коли 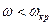( - критична кутова швидкість), будь-яке збурення (поштовх) приводить до все зростаючого відхилення від вертикалі; 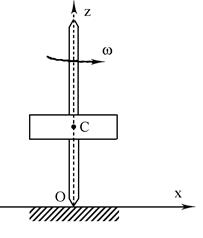якщо ω>ω_кp, то малі збурення практично не позначаються на напрямі осі. Отже, при ω<ω_кp гіроскоп по відношенню до напряму його осі буде нестійким, а при ω>ω_кp – стійким. Це і є умовою стійкості. При цьому

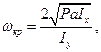(19.24)

де Р - вага гіроскопа, a – відстань від точки О до центра ваги С, І_x і І_y - моменти інерції гіроскопа відносно осей Ох і Оу відповідно. Іншим буде результат, якщо розглянути рух гіроскопа по відношенню до кута обертання φ навколо осі Oz. В незбуреному русі при відсутності тертя (опору) кут повороту φ=ωt. Якщо внаслідок поштовху кутова швидкість зміниться на величину ε, то в збуреному русі φ ₁ = (ω+ε) t. Різниця Δ φ=φ ₁ - φ= =εt не залежить від ω і з часом нескінченно зростає; тоді по відношенню до кута повороту φ рух гіроскопа буде нестійким при будь-яких значеннях кутової швидкості ω. Таким чином, один і той же рух по відношенню до одних з його характеристик може бути стійким, а по відношенню до інших - нестійким.

Дослідження положень відносної рівноваги.

Часто при дослідженні різних механізмів потрібно знайти положення відносної рівноваги і стійкість. Для цього складають так звану змінену потенціальну енергію системи W:

W=П+T, (19.25)

де П - потенціальна енергія, Т - кінетична енергія системи. Стан рівноваги (положення рівноваги) визначається з рівняння

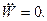(19.26)

Положення рівноваги буде стійким при

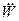>0. (19.27)

При 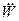<0 (19.28)

положення рівноваги є нестійким.

Дослідження стійкості руху по першому наближенню.

Метод визначення стійкості руху по першому наближенню полягає в наступному. Нехай

(19.29)

є частинними розв’язками системи диференціальних рівнянь першого порядку

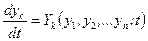(19.30)

при заданих початкових умовах руху

при t ₀=0. (19.31)

Розв’язок (19.29) визначає незбурений рух системи. При інших початкових умовах руху значення змінних у_k, які визначають подальший рух системи, записують так:

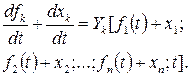(19.32)

Віднімемо від (19.32) рівняння (19.30) і знайдемо

(19.33)

Введемо позначення:

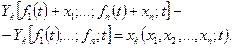(19.34)

Одержимо систему диференціальних рівнянь

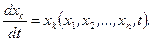(19.35)

З (19.34) виходить, що

x_k (0, 0,...,0; t) = 0 (19.36)

(х ₁ = х ₂ =...= х_n = 0) (19.37)

є частинним розв’язком системи (19.35), який відповідає незбуреному рухові.

Для розгляду стійкості руху по першому наближенню в системі рівнянь (19.35) в правій частині виділяють лінійні складові (доданки). Коли час явно не входить в праву частину рівняння, будемо мати

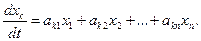(19.38)

Запишемо характеристичне рівняння системи (19.38):

(19.39)

Згідно першої теореми Ляпунова, незбурений рух, який визначається рівнянням (19.29), є стійким, коли корені характеристичного рівняння (19.39) мають від’ємну дійсну частину. В цьому випадку нелінійні доданки в правій частині рівнянь (19.38) не впливають на стійкість руху. Про знак кореня характеристичного рівняння можна судити на основі теореми Гурвіца, яка формулюється так: рівняння n -го степеня з дійсними коефіцієнтами (а ₀>0)

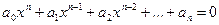(19.40)

має всі корені з від’ємною дійсною частиною, коли всі визначники вигляду

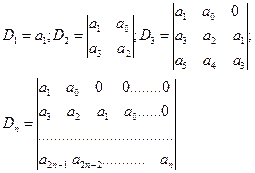
є додатними.

При розв’язуванні задач на дослідження стійкості руху системи по першому наближенню рекомендується такий порядок дій:

1) визначаємо число ступенів вільності системи і вибираємо узагальнені координати;

2) користуючись рівнянням Лагранжа, складаємо рівняння незбуреного руху;

3) складаємо рівняння збуреного руху, вважаючи, що узагальнені координати відрізняються від значень в незбуреному русі на величини першого порядку малості;

4) віднімаємо від диференціальних рівнянь збуреного руху відповідні рівняння незбуреного руху;

5) для системи лінійних диференціальних рівнянь з постійними коефіцієнтами складаємо характеристичне рівняння;

6) користуючись теоремою Гурвіца, визначаємо знаки дійсних частин коренів характеристичного рівняння і потім робимо висновок про стійкість руху системи.

Зауваження. Для закріплення матеріалу §19 (пункт 19.4) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 56.1 - 56.5;

2) № 56.7 – 56.15;

3) № 56.17 - 56.20.

Рекомендується розв’язати також задачі № 18.6, 18.7, 18.10, 18.12, 18.15, 18.19, 18.20, 18.24, 18.26, 18.27, 18.32 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Date: 2015-08-15; view: 506; Нарушение авторских прав