Малі коливання механічної системи з декількома ступенями вільності

Тут досліджуються малі коливання механічних систем, на які накладені голономні ідеальні та стаціонарні в’язі. Розглянемо систему з двома ступенями вільності. Узагальнені координати - q ₁ і q ₂. Кінетична енергія системи дорівнює

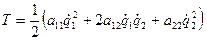(19.11)

Величини а ₁₁, а ₁₂, а ₂₂ називають інерційними коефіцієнтами. Рівняння Лагранжа другого роду мають вигляд

(19.12)

З урахуванням (19.11) рівняння (19.12) перепишемо так:

(19.13)

Частинний розв’язок рівнянь (19.13) шукаємо у вигляді:

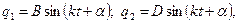(19.14)

де В, D, α - невідомі сталі. Для їх визначення знаходимо похідні від (19.14), скориставшись рівняннями (19.13), і одержимо

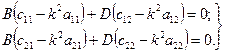(19.15)

Система рівнянь має відмінні від нуля розв’язки, якщо детермінант системи буде рівний нулю:

(19.16)

З рівнянь (19.15) знаходимо відношення амплітуд

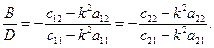(19.17)

З виразів (19.16) або (19.17) знайдемо рівняння частот (по іншому його називають віковим рівнянням):

(19.18)

Досліджувані рухи будуть малими, рівновага буде стійкою, якщо корені цього рівняння будуть додатними:

Якщо 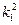чи від’ємні або є комплексними величинами, то розв’язки (19.14) включають гіперболічні функції і рух навколо положення рівноваги не буде малим. Корен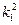і і будуть додатними тоді, коли виконуються нерівності

Після того, як корені рівняння частот k ₁ і k ₂ обчислені, знаходимо головні коливання системи. Перше головне коливання описується рівняннями

(19.19)

Друге головне коливання описується рівняннями

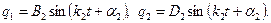(19.20)

Загальний розв’язок

(19.21)

Відношення амплітуд дорівнює

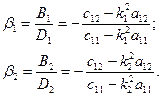(19.22)

Тоді

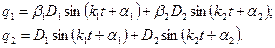(19.23)

Довільні сталі інтегрування D ₁, D ₂, α ₁, α ₂ визначаються з початкових умов. При розв’язанні задач на дослідження малих коливань консервативної системи з двома ступенями вільності рекомендується такий порядок дій:

1) вибрати узагальнені координати q ₁ і q ₂;

2) обчислити кінетичну енергію системи Т;

3) обчислити потенціальну енергію системи П або узагальнені сили;

4) знайти похідні від кінетичної енергії і скласти рівняння Лагранжа другого роду;

5) задати частинний розв’язок і підставити його в систему диференціальних рівнянь руху;

6) з одержаної в пункті 5) системи алгебраїчних рівнянь визначити амплітуди коливань і знайти рівняння частот;

7) розв’язати рівняння частот, знайти власні частоти коливань системи;

8) внести знайдені частоти в частинний розв’язок і одержати формули, які описують два головних коливання;

9) додавши рівняння головних коливань для кожної узагальненої координати, знайти загальний розв’язок;

10) з початкових умов знайти чотири довільні сталі інтегрування.

Зауваження. Для закріплення матеріалу §19 (пунктів 19.1 – 19.3) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 53.2, 53.4, 53.5, 54.1 - 54.5, 55.1 - 55.5, 55.7;

2) № 48.10, 48.19, 48.20, 48.35 - 48.37, 48.39, 53.6, 53.12 - 53.14, 54.10, 54.12, 54.20, 54.22, 54.32, 54.35, 55.9, 55.12, 55.15 – 55.17, 55.25;

3) № 53.15 - 53.18, 54.37 - 54.39, 54.40, 54.42, 54.48, 55.28, 55.36, 55.41, 55.44.

Рекомендується розв’язати також задачі № 14.5, 14.7, 14.15, 14.17, 14.28, 14.31, 14.38, 14.61, 14.63, 14.65, 14.75, 14.78, 14.82, 14.89 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Date: 2015-08-15; view: 361; Нарушение авторских прав