Рівняння Лагранжа першого роду

Розглянемо невільну матеріальну систему, що складається з n матеріальних точок. На систему накладено h голономних в’язей. Число ступенів вільності цієї системи визначається формулою

s=2n - h.

Якщо в’язі задані рівняннями

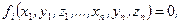(18.11)

де і= 1,2,3,..., h, то рівняння Лагранжа першого роду мають, вигляд

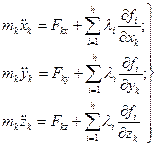(18.12)

(k= 1, 2 ,...,n; і =1, 2,..., h),

де F_kx, F_ky, F_kz - проекції на осі х, у, z рівнодійної активних сил, прикладених до k- тої матеріальної точки, λ_і - невизначені множники. Рівняння Лагранжа першого роду інколи називають рівняннями Лагранжа з множниками. Ці 3 n рівнянь (18.12) спільно з h рівняннями в’язей утворюють систему 3 n+h рівнянь з 3 n+h невизначеними невідомими (3 n координат, n матеріальних точок і h невизначених множників).

В рівняннях (18.12) виразимо:

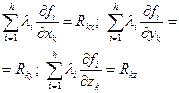(18.13)

(k =1, 2,..., n; і =1, 2,..., h),

де R_kx, R_ky, R_kz - проекції на вісі x, у, z рівнодійної реакцій в’язей, які діють на k- ту матеріальну точку.

Задачу на визначення законів руху точок системи і реакцій в’язей за допомогою рівнянь Лагранжа першого роду рекомендується розв’язувати в такій послідовності:

1) показати на рисунку активні сили;

2) вибрати систему декартових осей координат;

3) визначити проекції F_kx, F_ky, F_kz активних сил, прикладених до матеріальних точок, на декартові осі координат;

4) скласти рівняння в’язей, накладених на матеріальні точки системи f_і= 0 (і =1, 2,..., h);

5) обчислити частинні похідні від рівняннь в’язей за декартовими координатами матеріальної точки:

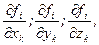де і =1, 2,..., h; k= 1, 2,..., n;

6) скласти систему 3 n рівнянь Лагранжа першого роду, в які ввійдуть h невизначених множників λ ₁, λ ₂,..., λ_h;

7) вибрати рівняння кількістю, рівною h, розв’язати ці рівняння відносно λ ₁, λ ₂,..., λ_h;

8) підставити одержані в пункті 7) значення h множників λ_і в останні 3 n-h рівнянь Лагранжа першого роду;

9) приєднати до цих 3 n-h рівнянь Лагранжа h рівнянь в’язей та інтегруванням визначити закон руху матеріальної точки (або точок матеріальної системи);

10) визначити проекції реакцій в’язей 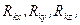де k =1, 2,..., n.

Зауваження. Для закріплення матеріалу §18 необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 47.1 - 47.7, 48.1, 48.3 - 48.7;

2) № 47.9 - 47.13, 47.15, 48.8, 48.9, 48.12, 48.16, 48.17, 48.21, 48.26 - 48.31, 48.41, 48.43;

3) № 47.16 - 47.19, 48.20, 48.24, 48.33, 48.34, 48.44, 48.46, 48.47 – 48.50, 48.52.

Рекомендується розв’язати також задачі № 12.2 - 12.4, 12.6, 12.10, 12.11, 12.18, 12.19, 12.21 - 12.24, 12.26, 12.29, 12.30 зі збірника “Сборник задач по теоретической механике /Под ред. К. С. Колесникова. – М., Наука, 1989”.

Date: 2015-08-15; view: 448; Нарушение авторских прав