Теорема про змiну кiлькостi руху (iмпульсу) точки. Методичнi вказiвки до розв’язання задач

Кількістю руху (імпульсом) матерiальної точки називають добуток маси точки та її швидкості:

(9.1)

За другим законом Ньютона маємо

d (m 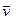) = 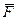·dt. (9.2)

Лiва частина формули (9.2) - геометрична змiна iмпульсу рухомої матерiальної точки за нескiнченно малий промiжок часу dt. У правiй частинi цiєї формули - добуток дiючої сили та нескiнченно малого промiжку часу її дiї:

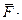dt = d . (9.3)

Це є елементарний iмпульс прикладеної сили. З (9.2) видно, що елементарний iмпульс прикладеної сили характеризує ту кiлькiсть руху, яка надходить вiд навколишнiх тiл до точки за нескiнченно малий промiжок часу.

Рiвняння (9.2) виражає теорему:

геометрична змiна кiлькостi руху (iмпульсу) матерiальної точки за нескiнченно малий промiжок часу дорiвнює елементарному iмпульсу прикладеної сили за той же промiжок часу.

При iнтегруваннi (9.2) одержимо:

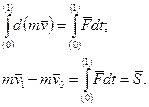(9.4)

Початкове положення матерiальної точки тут позначене значком (0), кiнцеве положення - (1).

Величина називається iмпульсом сили за даний скiнченний промiжок часу.

Рiвняння (9.4) виражає теорему:

геометричний прирiст кiлькостi руху (iмпульсу) рухомої матерiальної точки за скiнченний промiжок часу дорiвнює iмпульсу прикладеної сили за той же самий промiжок часу.

У проекцiях на осi декартової системи координат рiвняння (9.4) запишеться так:

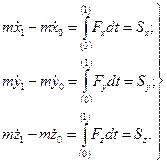(9.5)

Тобто, прирiст проекцiї вектора кiлькостi руху (iмпульсу) на кожну нерухому координатну вiсь дорiвнює проекцiї iмпульсу прикладеної сили за той же самий промiжок часу i на ту ж вiсь.

У випадку, коли 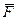= 0, з (9.2) витiкає, що m 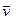= const. Це закон збереження iмпульсу матерiальної точки: якщо рiвнодiйна прикладених до матерiальної точки сил дорiвнює нулю, то iмпульс матерiальної точки зберiгається незмiнним за величиною i за напрямом.

При розв’язуваннi задач на застосування теореми про змiну кiлькостi руху матерiальної точки доцiльно дотримуватися таких методичних вказiвок:

1) вибрати об’єкт дослiдження, прийняти його за матерiальну точку, показати цю точку в довiльний момент часу (в промiжному положеннi), показати вектори швидкостей в початковий i кiнцевий моменти часу;

2) прикласти всi активнi (заданi) сили;

3) вiдкинути в’язi, замiнивши їх реакцiями;

4) вибрати систему координат;

5) скласти теорему про змiну кiлькостi руху в проекцiях на осi координат;

6) виразити всi члени, що входять в усi рiвняння, через вiдомi i шуканi величини;

7) розв’язати цi рiвняння вiдносно шуканих величин.

Зауваження. Для закріплення матеріалу §9 (пункт 9.1) необхідно розв’язати задачі зі збірника “Мещерский И. В. Сборник задач по теоретической механике. – М., Наука, 1981 (1986)”:

1) № 28.1, 28.2, 28.6;

2) № 28.5, 28.8, 28.12;

3) № 28.16, 28.17, 28.18, 28.20.

Date: 2015-08-15; view: 1053; Нарушение авторских прав