Общие приемы решения уравнений динамики упругих систем

Задачи динамики упругих систем заключаются в определении характера изменения и максимальных значений динамических нагрузок звеньев, частот колебаний, условий резонансного состояния системы.

Рассмотрим совместное решение двух линейных уравнений второго порядка. Эти уравнения описывают движение двухмассовой системы с упругой связью (рис. 16).

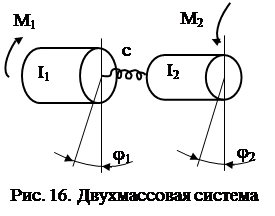Здесь:

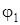и 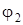– текущие углы поворота масс с 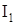и 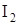, которые при наличии упругой связи не равны ;

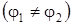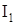‑ ведущая масса;

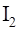‑ ведомая масса.

На массу I₁ действует некоторый момент M₁, а на массу I₁ ‑ момент M₂, представляющий статическое сопротивление, действующее на эту массу.

Система может прийти в движение в случае, когда 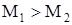. При пуске и торможении машины её разгон или торможение осуществляются за счет разности 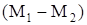. Поскольку 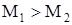, можем написать

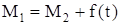, (101)

где f(t) – избыточная сила (момент), зависящая от времени и существующая в периоды неустановившихся процессов.

Дифференциальные уравнения движения масс I₁ и I₂

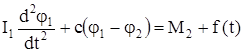, (102)

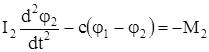(103)

Для решения системы уравнений (102) и (103), продифференцируем каждое из них

, (104)

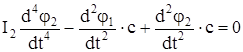. (105)

Суммируя эти уравнения, получим

, (106)

откуда

, (107)

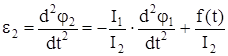. (108)

Подставляя значение (108) в уравнение (104), а (107) в (105), после преобразований получим

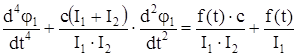, (109)

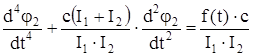. (110)

Решения уравнений (109) и (110) относительно вторых производных j₁ и j₂ по t в общем виде будет

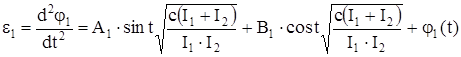, (111)

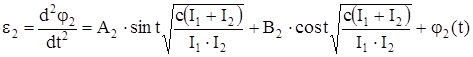, (112)

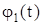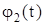где и – частные решения уравнений, зависящие от функции f(t).

С учетом формулы (62) выражения (111) и (112) можно представить в виде

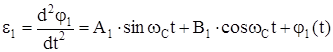, (113)

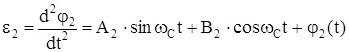. (114)

Дважды интегрируя уравнения (113) и (114), получим

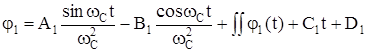, (115)

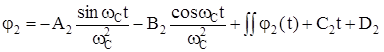. (116)

Зная режим разгона или торможения – 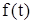, и, следовательно, имея возможность найти частные решения уравнений (113) и (114) 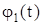и 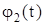, а также используя соотношения между 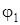, , 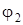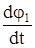и 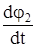из уравнений (102) и (103), запишем

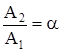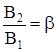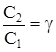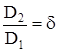; ; ; . (117)

Тогда можно записать выражения, содержащие одинаковые постоянные коэффициенты

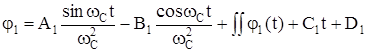, (118)

. (119)

Приняв начальные условия, действительные для разгона или торможения, подставив их в уравнения (118) и (119), найдем конкретные решения для j₁ и j₂.

Деформация упругого звена будет определяться разностью

.

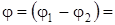
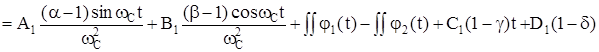(120)

Момент в упругой связи равен

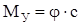, (121)

где c – приведенная жесткость рассматриваемой системы.

Date: 2015-08-15; view: 392; Нарушение авторских прав