
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Зависимость между напряжением и дефрмацией. Закон Гука. Испытнае материалов при растяжении
|
|
2.2. Напряжения и деформации
При растяжении стержня его длина увеличивается, а поперечные размеры уменьшаются (рис. 2.2). Изменение длины 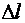 называется абсолютной продольной деформацией, а изменения поперечных размеров
называется абсолютной продольной деформацией, а изменения поперечных размеров  и
и 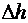 – абсолютными поперечными деформациями. По этим величинам вычисляют относительную продольную деформацию
– абсолютными поперечными деформациями. По этим величинам вычисляют относительную продольную деформацию 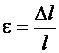 и относительную поперечную деформацию
и относительную поперечную деформацию 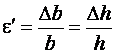 .
.
Опытами установлено, что отношение 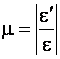 остаётся постоянным для каждого материала и находится в интервале 0...0,5.
остаётся постоянным для каждого материала и находится в интервале 0...0,5.
Параметр 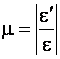 называется коэффициентом Пуассона.
называется коэффициентом Пуассона.
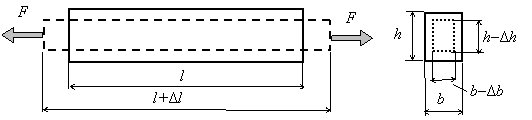
Рис. 2.2. Деформации растянутого стержня
В поперечных сечениях стержня возникают нормальные напряжения, которые, согласно гипотезе плоских поперечных сечений, равномерно распределены по всей площади сечения (рис. 2.3, а) и равны отношению продольной силы к площади поперечного сечения
 .
.
Между нормальными напряжениями и относительной продольной деформацией существует зависимость, называемая законом Гука:
 ,
,
в которой коэффициент пропорциональности Е называется модулем упругости. Модуль упругости определяется опытным путем и является важной характеристикой материала. Единицы измерения модуля упругости совпадают с единицами измерения напряжений (МПа, кН/см2).
Абсолютную продольную деформацию вычисляют по формуле
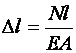 ,
,
где произведение ЕА называется жёсткостью при растяжении (сжатии).

Рис. 2.3. Нормальные напряжения в сечениях стержня:
а – в поперечном; б – в наклонном
Анализ напряженного состояния показывает, что в поперечных сечениях стержня действуют только нормальные напряжения, в продольных сечениях нет никаких напряжений, а в наклонных сечениях возникают нормальные и касательные напряжения. Наибольшие касательные напряжения равны половине нормальных напряжений в поперечном сечении и действуют на площадках, наклоненных под углом 45° к продольной оси стержня (рис. 2.3, б).
Различие в способах приложения внешних сил к стержню сказывается на распределении деформаций и напряжений только на сравнительно коротких участках стержня вблизи места приложения сил (рис. 2.4).
В этом заключается принцип Сен-Венана, подтверждаемый опытами.

Рис. 2.4. На левом участке стержня распределение напряжений
не зависит от способа приложения нагрузки
2.3. Испытания материалов на растяжение и сжатие
Для определения характеристик конструкционных материалов на специальных машинах и установках проводят испытания образцов, изготовленных из различных материалов. Форма, размеры образцов, порядок испытаний регламентируются техническими условиями для возможности сопоставления полученных результатов. В процессе испытаний фиксируются величины растягивающих или сжимающих сил, продольных деформаций, автоматически вычерчиваются диаграммы зависимости между деформациями образцов 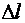 и усилиями в образцах
и усилиями в образцах  . От полученных диаграмм переходят к диаграммам напряжений, на которых по оси абсцисс откладывают относительную продольную деформацию образца
. От полученных диаграмм переходят к диаграммам напряжений, на которых по оси абсцисс откладывают относительную продольную деформацию образца 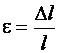 , а по оси ординат – нормальное напряжение
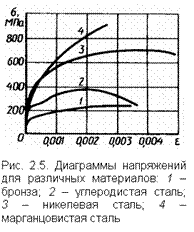
, а по оси ординат – нормальное напряжение  . Вид таких диаграмм показан на рис. 2.5.
. Вид таких диаграмм показан на рис. 2.5.
|
На диаграмме напряжений пластичной стали (рис. 2.6) можно отметить несколько точек, которые соответствуют механическим характеристикам прочности материала.
Предел пропорциональности 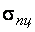 – наибольшее напряжение, при котором ещё справедлив закон Гука.
Предел упругости – наибольшее напряжение, при котором ещё справедлив закон Гука.
Предел упругости 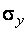 – напряжение, при котором относительная продольная остаточная деформация имеет малую величину (0,02...0,05 %).
Предел текучести – напряжение, при котором относительная продольная остаточная деформация имеет малую величину (0,02...0,05 %).
Предел текучести 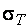 – напряжение, при котором деформации возрастают без увеличения усилия в образце. Если площадка текучести (горизонтальный участок на диаграмме напряжений) отсутствует или выражена неявно, то определяют условный предел текучести σ0,2 – напряжение, при котором остаточная деформация равна 0,2 %.
Временное сопротивление (предел прочности) – напряжение, при котором деформации возрастают без увеличения усилия в образце. Если площадка текучести (горизонтальный участок на диаграмме напряжений) отсутствует или выражена неявно, то определяют условный предел текучести σ0,2 – напряжение, при котором остаточная деформация равна 0,2 %.
Временное сопротивление (предел прочности) 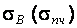 – напряжение, соответствующее наибольшей нагрузке на образец.
Тангенс угла наклона прямолинейного участка ОА на диаграмме напряжений (рис. 2.6) равен модулю упругости материала. – напряжение, соответствующее наибольшей нагрузке на образец.
Тангенс угла наклона прямолинейного участка ОА на диаграмме напряжений (рис. 2.6) равен модулю упругости материала.
|
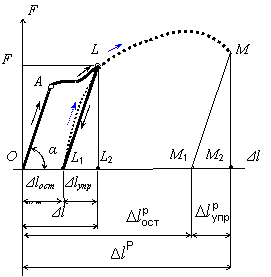
Пусть некоторой точке L на диаграмме растяжения (рис. 2.7) соответствует усилие в стержне F и удлинение образца Δl. При разгрузке образца график будет изображаться прямой LL1, проходящей параллельно начальному участку диаграммы ОА. Отрезок OL1 равен остаточной деформации 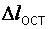 , а отрезок L1L2 равен упругой деформации
, а отрезок L1L2 равен упругой деформации 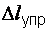 . Полная деформация, соответствующая точке L, получается как сумма
. Полная деформация, соответствующая точке L, получается как сумма
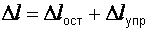 .
.
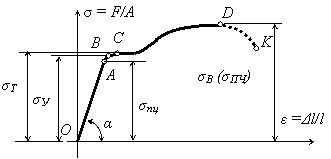
| 
|
| Рис. 2.6. Диаграмма напряжений пластичной стали | Рис. 2.7. Диаграмма растяжения при повторном нагружении |
При повторном нагружении образца диаграмма, показанная на рис. 2.7 пунктиром, будет вначале изображаться слабо искривленной линией L1L, а после достижения точки L пойдет так, как будто не было разгрузки и повторного нагружения. Криволинейность участка L1L вызывается необратимыми потерями энергии деформации, а сама кривая L1L называется петлей гистерезиса. Во многих случаях искривленностью участка L1L пренебрегают и считают его прямолинейным.
Разрыву образца соответствует точка М. Полная деформация ΔlР, предшествующая разрыву, изображается отрезком ОМ2, а после разрушения образца можно измерить остаточную деформацию 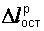 , равную отрезку ОМ1.
, равную отрезку ОМ1.
Диаграмма напряжений при разгрузке и повторном нагружении имеет аналогичный вид (рис. 2.8). После нагружения образца выше площадки текучести, разгрузки и при повторном нагружении изменяются некоторые свойства материала:
повышается предел пропорциональности (от величины 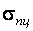 до величины
до величины 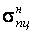 );
);
исчезает площадка текучести;
уменьшается деформация, предшествующая разрушению (отрезок L1M2 вместо отрезка ОМ2), поэтому материал становится менее пластичным.
Указанные изменения свойств называются наклепом.
Наклеп может быть полезен, например, для уменьшения деформаций тросов и цепей грузоподъемных машин, или вреден, например, при динамических нагрузках.
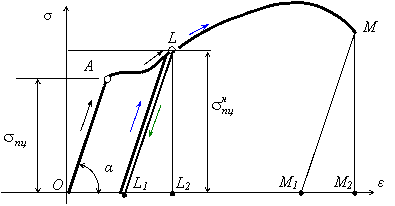
Рис. 2.8. Диаграмма напряжений при повторном нагружении
Перед испытанием образца измеряют его расчетную длину L0 и размеры поперечного сечения, по которым находят начальную площадь поперечного сечения А0.
После разрыва образца измеряют новую длину L1 и новые размеры поперечного сечения в месте разрыва для вычисления площади поперечного сечения А1.
Вычисляют характеристики пластичности материала:
относительное остаточное удлинение 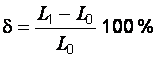 ;
;
относительное остаточное сужение 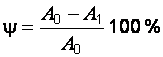 .
.
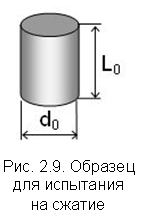
| Для испытания на сжатие изготовляют стальные и чугунные цилиндрические образцы (рис. 2.9) диаметром d0 = 6…25 мм. Отношение L0 / d0 = 1…2. Диаграмма сжатия стального образца (рис. 2.10, а) начинается с прямолинейного участка ОА, затем график искривляется, площадка текучести явно не выражается даже для пластичной стали. При испытаниях определяют усилия FП и FТ, по которым вычисляют предел пропорциональности П = FП/А0 и предел текучести Т = FТ/А0. Если площадка текучести выражена неявно, то определяют условный предел текучести 0,2 как напряжение, соответствующее остаточной деформации ε = 0,2 %. Величины предела пропорциональности и предела текучести стали при сжатии оказываются близкими к их значениям при растяжении. Стальной образец при сжатии сплющивается, не разрушаясь. |
Предел прочности стали при сжатии не определяется и условно принимается равным пределу прочности при растяжении.
Диаграмма сжатия чугунного образца не имеет ярко выраженного прямолинейного участка и, постепенно искривляясь, обрывается в момент разрушения образца (рис. 2.10, б).
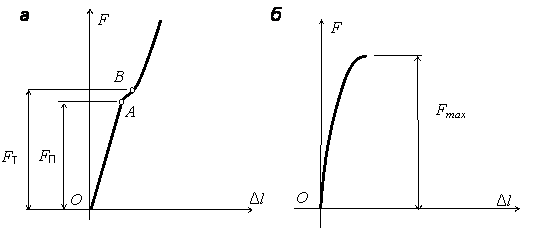
Рис. 2.10. Диаграммы сжатия образцов: а – стального; б – чугунного
Для чугуна вычисляют предел прочности при сжатии 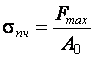 , где , где  – площадь поперечного сечения образца до испытания.
Продольные деформации чугунного образца незначительны. Образец получает слабовыраженную бочкообразную форму, на нем появляются трещины, наклоненные под углом 45 к оси образца. Разрушение происходит путем среза по одной из наклонных площадок (рис. 2.11). – площадь поперечного сечения образца до испытания.
Продольные деформации чугунного образца незначительны. Образец получает слабовыраженную бочкообразную форму, на нем появляются трещины, наклоненные под углом 45 к оси образца. Разрушение происходит путем среза по одной из наклонных площадок (рис. 2.11).
|
Date: 2015-08-15; view: 3666; Нарушение авторских прав