Растяжение-сжатие прямолинейных стержней

Осевым растяжением (сжатием) называется такой вид деформации стержня, при котором в поперечных сечениях возникает только продольная сила N.Растягивающие продольные силы считаются положительными, а сжимающие – отрицательными. График, показывающий изменение продольной силы вдоль оси стержня, называется эпюрой продольных сил (Эп.N). Для построения Эп.N стержень разделяют на участки, на каждом из которых находят продольную силу методом сечений как функцию внешних сил и координаты Z, определяющей положение поперечного сечения. Затем строят графики полученных функций.

Пример 2.1. Стержень (рис. 2.1, а) для построения эпюры продольных сил разделяем на два участка. Проведя на верхнем участке произвольное сечение 1–1, выделяем верхнюю часть стержня, заменяя действие нижней части положительной продольной силой N₁ (рис. 2.1, б). Из уравнения равновесия в виде 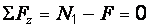находимN₁ = F = 8 кН при любом значении z₁. График этой функции – прямая, параллельная оси z. Нижний участок стержня рассекаем сечением 2–2, выделяем верхнюю часть стержня, заменяя действие нижней части положительной продольной силой N₂ (рис. 2.1, в). Из уравнения равновесия в виде 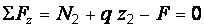получаем N₂ =
= 8–10 z₂ при 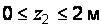. График этой функции – наклонная прямая с ординатами на концах участка 8 и –12 кН (рис. 2.1, г).

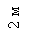
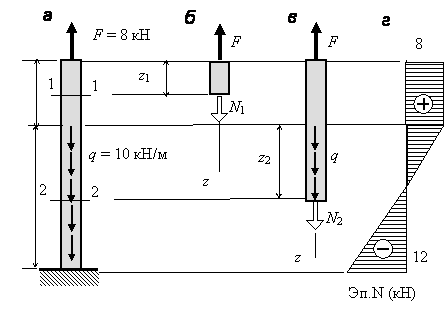
Рис. 2.1. Построение эпюры продольных сил: а – заданный
стержень; б, в – отсеченные части стержня; г – эпюра N

2.2. Напряжения и деформации

При растяжении стержня его длина увеличивается, а поперечные размеры уменьшаются (рис. 2.2). Изменение длины 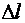называется абсолютной продольной деформацией, а изменения поперечных размеров и 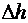– абсолютными поперечными деформациями. По этим величинам вычисляют относительную продольную деформацию 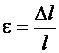и относительную поперечную деформацию .

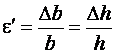Опытами установлено, что отношение 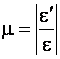остаётся постоянным для каждого материала и находится в интервале 0...0,5.

Параметр 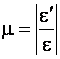называется коэффициентом Пуассона.

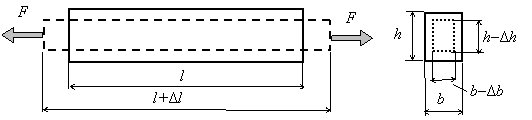
Рис. 2.2. Деформации растянутого стержня

В поперечных сечениях стержня возникают нормальные напряжения, которые, согласно гипотезе плоских поперечных сечений, равномерно распределены по всей площади сечения (рис. 2.3, а) и равны отношению продольной силы к площади поперечного сечения

.

Между нормальными напряжениями и относительной продольной деформацией существует зависимость, называемая законом Гука:

,

в которой коэффициент пропорциональности Е называется модулем упругости. Модуль упругости определяется опытным путем и является важной характеристикой материала. Единицы измерения модуля упругости совпадают с единицами измерения напряжений (МПа, кН/см²).

Абсолютную продольную деформацию вычисляют по формуле

,

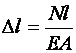где произведение ЕА называется жёсткостью при растяжении (сжатии).

Рис. 2.3. Нормальные напряжения в сечениях стержня:
а – в поперечном; б – в наклонном

Анализ напряженного состояния показывает, что в поперечных сечениях стержня действуют только нормальные напряжения, в продольных сечениях нет никаких напряжений, а в наклонных сечениях возникают нормальные и касательные напряжения. Наибольшие касательные напряжения равны половине нормальных напряжений в поперечном сечении и действуют на площадках, наклоненных под углом 45° к продольной оси стержня (рис. 2.3, б).

Различие в способах приложения внешних сил к стержню сказывается на распределении деформаций и напряжений только на сравнительно коротких участках стержня вблизи места приложения сил (рис. 2.4).
В этом заключается принцип Сен-Венана, подтверждаемый опытами.

Рис. 2.4. На левом участке стержня распределение напряжений
не зависит от способа приложения нагрузки

Date: 2015-08-15; view: 893; Нарушение авторских прав