Критерий минимаксного риска Сэвиджа в теории принятия решений в условиях полной неопределенности. Алгоритм выбора оптимальной стратегии на основе данного критерия

Критерий Сэвиджа (критерий потерь от «минимакса») предполагает, что из всех возможных вариантов «матрицы решений» выбирается та альтернатива, которая минимизирует размеры максимальных потерь по каждому из возможных решений. При использовании этого критерия «матрица решения» преобразуется в «матрицу потерь» (один из вариантов «матрицы риска»), в которой вместо значений эффективности проставляются размеры потерь при различных вариантах развития событий. Критерий Сэвиджа используется при выборе рисковых решений в условиях неопределенности, как правило, субъектами, не склонными к риску.

Критерий Байеса максимального среднего выигрыша в теории принятия решений в условиях статистической неопределенности. Алгоритм выбора оптимальной стратегии на основе данного критерия

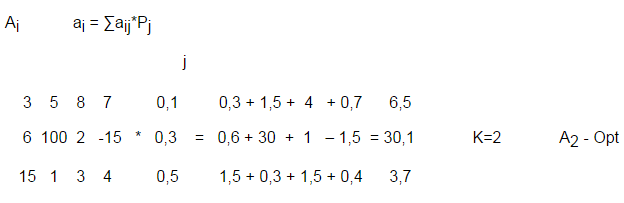
По критерию Байеса за оптимальные принимается та стратегия (чистая) Ai, при которой максимизируется средний выигрыш a или минимизируется средний риск.

Байесовское решение является оптимальным не в каждом отдельном случае, а в среднем. Такого рода оптимальность реально может проявить себя лишь при многократном проведении операции, когда среднее значение постепенно стабилизируется. Применение критерия Байеса оправданно, если ситуация, в которой принимается решение, характеризуется признаками: вероятности состояний природы известны и не зависят от времени; решение реализуется большое (теоретически бесконечное) число раз.

Показатель оптимальности стратегии - величина среднего выигрыша.

За оптимальную стратегию принимается чистая стратегия, при которой максимизируется средний выигрыш статистика

Показатель оптимальности стратегии - величина среднего риска.

За оптимальную стратегию принимается чистая стратегия, при которой минимизируется средний риск

Критерий недостаточных оснований Лапласа максимального среднего выигрыша в теории принятия решений в условиях статистической неопределенности. Алгоритм выбора оптимальной стратегии на основе данного критерия.

В основе критерия лежит предположение: поскольку о состояниях обстановки ничего не известно, то их можно считать равновероятными.

Kопт = max K(ai).

Рассчитаем эффективность систем по данному критерию для приведенного примера:

К(а1) = 0,25 (0,1 + 0,5 + 0,1 + 0,2) = 0,225;

К(а2) = 0,25 (0,2 + 0,3 + 0,2 + 0,4) = 0,275;

К(а3) = 0,25 (0,1 + 0,4 + 0,4 + 0,3) = 0,3

Оптимальное решение — система а3. Критерий Лапласа представляет собой частный случай критерия среднего выигрыша.

Если состояния Пj природы в равной мере правдоподобны, то их полагают равновероятными, т.е. q₁ = … = q_n = 1/n.

Показатель оптимальности стратегии - величина среднего выигрыша.

Оптимальной считается чистая стратегия A_i, обеспечивающая максимум среднего выигрыша при одинаковых априорных вероятностях Применение критерия Лапласа оправданно, если ситуация, в которой принимается решение, характеризуется признаками:

вероятности состояний природы неизвестны, не зависят от времени и равны;

решение реализуется большое (теоретически бесконечное) число раз;

для небольшого числа реализаций допускается некоторый неоцениваемый риск.

Основные понятия теории планирования идеального эксперимента в условиях статистической неопределенности. Формулы расчета гипотетического среднего выигрыша и цены достоверной информации в идеальном эксперименте. Условие проведения идеального эксперимента.

Идеальный эксперимент предполагает изменение экспериментатором только независимой переменной, зависимая переменная контролируется. Другие условия эксперимента остаются неизменными. Идеальный эксперимент предполагает эквивалентность испытуемых, неизменность их характеристик во времени, отсутствие самого физического времени (как это ни парадоксально звучит), возможность проводить эксперимент бесконечно. Следствием этого является проведение всех экспериментальных воздействий одновременно. Идеальный эксперимент противостоит реальному, в котором изменяются не только интересующие исследователя переменные, но и ряд других условий. Соответствие идеального эксперимента реальному выражается в такой его характеристике, как достоверность результатов, которую обеспечивает реальный эксперимент по сравнению с идеальным.

Понятие “идеальный эксперимент” ввел в употребление Д. Кэмпбелл. Идеальный эксперимент предполагает изменение экспериментатором только независимой переменной, зависимая переменная контролируется. Другие условия эксперимента остаются неизменными. Идеальный эксперимент предполагает эквивалентность испытуемых, неизменность их характеристик во времени, отсутствие самого физического времени (как это ни парадоксально звучит), возможность проводить эксперимент бесконечно. Следствием этого является проведение всех экспериментальных воздействий одновременно.

Идеальный эксперимент противостоит реальному, в котором изменяются не только интересующие исследователя переменные, но и ряд других условий. Соответствие идеального эксперимента реальному выражается в такой его характеристике, как внутренняя валидьость (validitу) – достоверность результатов, которую обеспечивает реальный эксперимент по сравнению с идеальным. Внутренняя валидность характеризует меру влияния на изменение зависимой переменной тех условий (независимой переменной), которые варьирует экспериментатор (рис. 4.4).

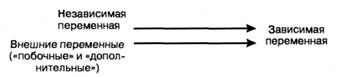
Чем больше влияют на изменение зависимой переменной неконтролируемые исследователем условия, тем ниже внутренняя валидность эксперимента. Следовательно, больше вероятность того, что факты, обнаруженные в эксперименте, являются артефактами.

Планирование эксперимента необходимо для выявления влияния независимой переменной на зависимую за счет контроля других переменных. Переменные, являющиеся источником артефактов, либо устраняются, либо их влияние усредняется (за счет смешения и погашения изменчивости условий эксперимента). Высокая внутренняя валидность – главный признак хорошего эксперимента (близко к “безупречному эксперименту”).

Не все переменные, влияющие на результат исследования, можно учесть или исключить (элиминировать). Те из них, которые нарушают внутреннюю валидность, называют “побочными”. К числу побочных, полностью не устранимых переменных относят влияние фактора времени, фактор задачи, фактор индивидуального различия.

Рассмотрим более подробно центральное понятие “валидность”. Обратимся к системе отношений “эксперимент–теория–реальность”. На основе теории выдвигается гипотеза, которая в конечном счете и проверяется в эксперименте. Методики и план эксперимента должны соответствовать проверяемой гипотезе – степень этого соответствия и характеризует операциональную валидность. Например, в эксперименте по научению резкий звук зуммера используется как эквивалент “наказания” за ошибку, поэтому возникает сомнение в правильности такой интерпретации. В самом эксперименте мы должны максимально учесть, устранить и т. д. влияние побочных переменных на зависимую переменную. Внутренняя валидность характеризует меру влияния независимой переменной на зависимую по отношению к другим факторам. Иными словами, внутренняя валидность тем выше, чем больше вероятность того, что экспериментальный эффект (изменение зависимой переменной) вызван изменением независимой переменной.

Эксперимент должен воспроизводить внешнюю реальность. Эксперимент, который полностью воспроизводит внешнюю реальность, называется экспериментом полного соответствия. Разумеется, в реальности полное соответствие недостижимо. Мера соответствия экспериментальной процедуры реальности характеризует внешнюю валидность эксперимента.

Дополнительные переменные, которые требуют учета в эксперименте, влияют на внешнюю валидность. Если от внутренней валидности зависит достоверность экспериментальных результатов, то от внешней – переносимость результатов из лабораторных условий на реальные процессы и обобщение их на другие сферы реальности.

Наконец, связь теории и реальности отражается в адекватности теории реальности и прогностичности ее предсказаний. Кэмпбелл ввел еще одно важное понятие, характеризующее валидность эксперимента, а именно – конструктивную валидность. Конструктная валидность выражает адекватность метода интерпретации экспериментальных данных теории, т. е. в структуру следует ввести четвертую составляющую – интерпретацию: теория–эксперимент–интерпретация–реальность.

Конструктная валидность, по мнению Кэмпбелла, характеризует правильность обозначения (интерпретации) причины и экспериментального эффекта с помощью абстрактных терминов из обыденного языка или формальной теории.

Таким образом, внутренняя валидность определяется достоверностью интерпретации экспериментального эффекта как связи изучаемой причины и следствия (отношение эксперимент–интерпретация), а конструктная валидность – правильностью употребления терминов той или иной теории при интерпретации данных эксперимента.

Кэмпбелл отмечает, что установление внутренней валидности требует отбраковывания альтернативных объяснений связи между зависимой и независимой переменными. Установление конструктивной валидности требует отказа от альтернативных интерпретаций соотношения причины и следствия с понятиями, взятыми из той или иной теории. С точки зрения Кэмпбелла, хороший эксперимент должен:

1) выявлять временную последовательность предполагаемых причины и следствия;

2) показывать, что вероятные причины и эффект взаимосвязаны (ковариантны);

3) исключать влияние побочных переменных, которым можно было бы объяснить экспериментальный эффект; 4) исключать альтернативные гипотезы о теоретических конструктах, объясняющих эту связь.

Для уяснения отношений между основными характеристиками экспериментального исследования полезно запомнить следующую схему: (см. рис. 4.5).

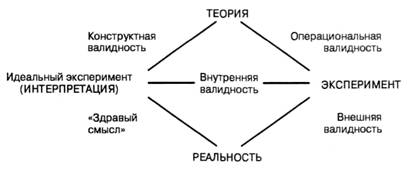
Внутренняя валидность является непременным условием любого эксперимента. Кэмпбелл выделил восемь основных факторов, нарушающих внутреннюю валидность эксперимента. Перечислим их. Первую группу можно назвать факторами выборки:

1. Селекция – неэквивалентность групп по составу, которая вызывает систематическую ошибку в результатах.

2. Статистическая регрессия – частный случай ошибки селекции, когда группы отбирались на основе “крайних” показателей (иначе – корреляция из-за неоднородности группы).

3. Экспериментальный отсев – неравномерное выбывание испытуемых из сравниваемых групп, приводящее к неэквивалентности групп по составу.

4. Естественное развитие – изменение испытуемых, являющееся следствием течения времени, без связи с конкретными событиями: изменение состояния (голод, усталость, болезнь и др.), свойств индивида (возрастные перемены, накопление опыта и др.).

Вторая группа – побочные переменные, влияние которых приводит к следующим эффектам:

1. Эффект “истории”– конкретные события, происходящие в период между начальным и итоговым тестированием помимо экспериментального воздействия.

2. Эффект тестирования – влияние предварительного тестирования на результат итогового.

3. Инструментальная погрешность – определяется надежностью метода фиксации поведения испытуемого, т. е. надежностью теста; именно надежность влияет на валидность, по утверждению Кэмпбелла, а не наоборот.

4. Взаимодействие факторов: отбора; естественного развития; истории (разные истории экспериментальных групп) и др.

Позже Кэмпбелл описал еще ряд источников нарушения внутренней валидности. Наиболее существенные относятся к экспериментальной процедуре, а именно: компенсаторное сопоставление эффектов различных воздействий, имитация воздействия, когда его на самом деле не происходит и др.

Понятие эквивалентности критериев в теории принятия решений в условиях неопределенности. Эквивалентность критерия Байеса максимального среднего выигрыша критерию минимальных средних потерь в теории принятия решений в условиях статистической неопределенности. (см методичку Систем анализ стр. 280)

41. Понятие «модель». Классификация моделей и требования к моделям экономических систем. Оценка точности и надежности результатов моделирования. (стр. 357).

Модель (франц.) — аналог или образец чего-либо, условный образ объекта исследования. Например, объектом исследования в сервисе являются си- стемы обслуживания клиентов. Слово “образ” означает не зеркальное отображение объекта исследования, а отображение основных его свойств, существен- ных для целей исследования. Все остальные свойства объекта не изучаются, и предполагается, что они удовлетворяют каким- либо условиям. Создание образа объекта всегда сопровождается его упрощением и идеализацией с помощью наложения на объект изучения определенных ограничений и условий. Слово “условный” означает наложение каких-либо условий, ограничений на объект исследования, позволяющих его упро- стить и идеализировать. Создание условного образа системы обслуживания (объекта) означает наложение на объект изучения следующих условий на свойства переменных как внутри объекта, так и в окружающей его среде: • система находится в состоянии динамического равновесия, при нормальной (эффективной) работе всех ее элементов; 358 359 • переменные системы имеют определенный закон рас- пределения; • вероятность того, что число заявок, поступающих на об- служивание за промежуток времени продолжительностью t, равно k, определяется по закону Пуассона; • выходной поток заявок подчиняется показательному за- кону распределения; • время ожидания в очереди подчиняется экспоненциаль- ному закону распределения1; • стоимость покупки однородных товаров подчиняется нор- мальному закону распределения; • имеются основные и второстепенные факторы, которые соответственно влияют на основные и вспомогательные функции деятельности объекта; • предполагается, что значения факторов находятся в гра- ницах допустимых значений; • изучаемая система является управляемой. Предметом исследования могут быть функциональные связи, которые имеются в системе. Для их отображения исполь- зуются математические модели. Математические модели — совокупность математических средств, с помощью которых отображаются функциональные зависимости элементов объекта изучения. Моделирование — процесс разработки модели, а также процесс ее использования для получения количественно- качественных характеристик какого-либо процесса или явления. Структура модели характеризует совокупность элементов и отношений между ними. Прогноз — то, что может произойти (в будущем) в резуль- тате применения системы. Прогнозирование — это общая категория, процесс получе- ния прогноза. Модель используется для получения параметров прогноза. 1 Спирин А. А., Фомин Г. П. Экономико-математические методы и модели в торговле. — М.: Экономика, 1988. — С. 62. Критерий — мерило чего-либо. Кэ =макс f (Ф1,Ф2,Ф3,В1,В2,В3), или f (Ф1,Ф2,Ф3,В1,В2,В3) ≤ Кэ *, где Ф1,..., Фn — параметры, характеризующие условия эконо- мического процесса; B1,..., Bn — параметры, характеризующие вариант деятель- ности системы (управления); Кэ,Кэ * — вычисленное и нормативное значения критериев соответственно. Например, критериями могут быть значение максимальной прибыли предприятия или же прибыль предприятия, при кото- рой оно находится на границе финансовой устойчивости. “Тело модели” — то, что является носителем информации, и то, что преобразует ее (математические, реальные физические материалы и т. д.). Функциями моделирования являются: описание, объясне- ние и прогнозирование поведение реальной системы, а также улучшение процессов. Цели моделирования: поиск оптимальных решений; оценка эффективности решения; определение свойств системы. В исследовании и моделировании экономических систем обычно выделяются три уровня использования количественных методов: измерение, математическое моделирование и принятие решений. Уровень измерений — количественное представление пере- менных и количественных закономерностей. Математическое моделирование — описание результатов измерения математи- ческими зависимостями. Принятие решений — поиск значений переменных, оптимизирующих объекты в заданном направле- нии. Все три уровня взаимно обуславливают и дополняют друг друга, но при этом каждый имеет свою специфику. Экономико-математическая модель, выступая в роли ин- струмента исследования, должна не только описывать состояние объекта заранее установленным способом, но и способствовать его изменению, а также получению оценки результатов такого изме- нения, т. е. должна носить нормативно-оценочный характер. 358 359 • переменные системы имеют определенный закон рас- пределения; • вероятность того, что число заявок, поступающих на об- служивание за промежуток времени продолжительностью t, равно k, определяется по закону Пуассона; • выходной поток заявок подчиняется показательному за- кону распределения; • время ожидания в очереди подчиняется экспоненциаль- ному закону распределения1; • стоимость покупки однородных товаров подчиняется нор- мальному закону распределения; • имеются основные и второстепенные факторы, которые соответственно влияют на основные и вспомогательные функции деятельности объекта; • предполагается, что значения факторов находятся в гра- ницах допустимых значений; • изучаемая система является управляемой. Предметом исследования могут быть функциональные связи, которые имеются в системе. Для их отображения исполь- зуются математические модели. Математические модели — совокупность математических средств, с помощью которых отображаются функциональные зависимости элементов объекта изучения. Моделирование — процесс разработки модели, а также процесс ее использования для получения количественно- качественных характеристик какого-либо процесса или явления. Структура модели характеризует совокупность элементов и отношений между ними. Прогноз — то, что может произойти (в будущем) в резуль- тате применения системы. Прогнозирование — это общая категория, процесс получе- ния прогноза. Модель используется для получения параметров прогноза. 1 Спирин А. А., Фомин Г. П. Экономико-математические методы и модели в торговле. — М.: Экономика, 1988. — С. 62. Критерий — мерило чего-либо. Кэ =макс f (Ф1,Ф2,Ф3,В1,В2,В3), или f (Ф1,Ф2,Ф3,В1,В2,В3) ≤ Кэ *, где Ф1,..., Фn — параметры, характеризующие условия эконо- мического процесса; B1,..., Bn — параметры, характеризующие вариант деятель- ности системы (управления); Кэ,Кэ * — вычисленное и нормативное значения критериев соответственно. Например, критериями могут быть значение максимальной прибыли предприятия или же прибыль предприятия, при кото- рой оно находится на границе финансовой устойчивости. “Тело модели” — то, что является носителем информации, и то, что преобразует ее (математические, реальные физические материалы и т. д.). Функциями моделирования являются: описание, объясне- ние и прогнозирование поведение реальной системы, а также улучшение процессов. Цели моделирования: поиск оптимальных решений; оценка эффективности решения; определение свойств системы.

Классификация модели:

По признаку средств моделирования можно выделить ма- териальные (физические) и абстрактные модели. Материальные модели воспроизводят основные геометри- ческие, физические, динамические и функциональные харак- теристики изучаемого явления или объекта с помощью матери- альных средств. С помощью таких моделей можно моделировать поиск оптимального варианта размещения технологического и тор- гового оборудования, потока покупателей, путей перемещения товаров. Материальное моделирование носит по своей природе экспериментальный характер. Пример. Можно определить разные варианты размещения оборудования на выделенной территории с помощью моделиро- вания размещения макетов оборудования и выбора оптимального варианта их размещения, удовлетворяющего определенному критерию. Абстрактные модели — плод человеческого мышления. По способам моделирования абстрактные модели подраз- деляются на три вида: графические, словесно-описательные и математические. Графические модели — визуальное представление с помо- щью графиков, диаграмм, схем исходных данных и результатов их обработки; информационных потоков; структуры предпри- ятия и процессов. Носителям графических моделей могут быть бумага, пленка, изображение на экране дисплея и настенном экране. Использование графических моделей позволяет получить следующие преимущества: • быстро и в полном объеме воспроизводится информация, которая нужна для принятия решения; • график исходных данных позволяет визуально опреде- лить все виды регулярностей, которые в них имеются, гораздо эффективнее, чем любые математические модели; • позволяет уменьшить размер доклада в два-три раза. Имеются определенные требования к построению графи- ческих изображений: • количество элементов на рисунке должно быть около 7, но не больше 10; • ширина и высота рисунка должны быть равны соотноше- нию “золотого сечения”, соответственно 5 и 3; • размер элементов рисунка должен обеспечить их види- мость всем зрителям. 362 363 • Класс (3.3) — целевые требования к модели: способность сохранять свою структуру во времени и при увеличении числа выделяемых факторов; сохранение собственного смысла каждого индикатора в модели и др. Перечисленные требования служат основанием при разра- ботке принципов конструирования и оценки качества моделей, предназначенных для экономического анализа — аналитиче- ских моделей. Назначение аналитической модели — обеспечение обра- ботки экономической информации с целью предоставления ее в наглядной форме для удобства экономического анализа и при- нятия управленческих решений. Аналитическая модель должна фиксировать значения эко- номических показателей и устанавливать факт их соответствия (несоответствия) норме (цели, критерию, прогнозу и т. п.), что обеспечивает диагностику и контроль предприятия. Кроме этого аналитическая модель должна обеспечить интерпретацию по- лученных данных и формирование содержательных выводов из них. Это касается прежде всего оценки результатов хозяй- ственной деятельности, которые выступают связующим звеном между анализом и принятием решений. Необходимым признаком аналитической модели выступает также создание информацион- ных условий для выявления основных экономических проблем и факторов улучшения или ухудшения результатов хозяйственной деятельности. Для получения таких сведений необходима разра- ботка соответствующих методов оценки, которые должны не толь- ко пассивно отражать фактическое состояние, но и способствовать своевременному принятию решений для внесения коррективов в стратегию и тактику хозяйственной деятельности. 11.1.2. Классификация моделей По признаку средств моделирования можно выделить ма- териальные (физические) и абстрактные модели. Материальные модели воспроизводят основные геометри- ческие, физические, динамические и функциональные харак- теристики изучаемого явления или объекта с помощью матери- альных средств. С помощью таких моделей можно моделировать поиск оптимального варианта размещения технологического и тор- гового оборудования, потока покупателей, путей перемещения товаров. Материальное моделирование носит по своей природе экспериментальный характер. Пример. Можно определить разные варианты размещения оборудования на выделенной территории с помощью моделиро- вания размещения макетов оборудования и выбора оптимального варианта их размещения, удовлетворяющего определенному критерию. Абстрактные модели — плод человеческого мышления. По способам моделирования абстрактные модели подраз- деляются на три вида: графические, словесно-описательные и математические. Графические модели — визуальное представление с помо- щью графиков, диаграмм, схем исходных данных и результатов их обработки; информационных потоков; структуры предпри- ятия и процессов. Носителям графических моделей могут быть бумага, пленка, изображение на экране дисплея и настенном экране. Использование графических моделей позволяет получить следующие преимущества: • быстро и в полном объеме воспроизводится информация, которая нужна для принятия решения; • график исходных данных позволяет визуально опреде- лить все виды регулярностей, которые в них имеются, гораздо эффективнее, чем любые математические модели; • позволяет уменьшить размер доклада в два-три раза. Имеются определенные требования к построению графи- ческих изображений: • количество элементов на рисунке должно быть около 7, но не больше 10; • ширина и высота рисунка должны быть равны соотноше- нию “золотого сечения”, соответственно 5 и 3; • размер элементов рисунка должен обеспечить их види- мость всем зрителям. 364 365 Словесно-описательные — комплекс слов, характеризую- щих поведение изучаемого явления или объекта, правила по- ведения человека в различных жизненных ситуациях. Приме- рами словесно-описательных моделей могут быть технические задания, пояснительные записки, обзоры коньюктуры рынка и конкурентов, общая характеристика магазина. Словесно- описательные модели позволяют достаточно полно на качествен- ном уровне описывать объект управления. Пример. Приведем словесно-описательную модель сервис- ной организации. Сервисная организация существует в пространстве и во вре- мени в правовой и законодательной среде общества в сочетании с потребностями своих сотрудников, существующих и будущих кли- ентов при соблюдении закона сохранения ресурсов: финансовых, людских, материальных, духовных, моральных и этических. Математические модели — совокупность математических средств, отображающих функциональные зависимости элемен- тов объекта изучения. Математические модели подразделяются на детермини- рованные (определенные) и стохастические (вероятностные или неопределенные). Детерминированные (определенные) модели характерны тем, что результат решения задачи полностью предопределяется заданным набором исходных данных. Стохастические (вероятностные или неопределенные) модели описывают такие процессы, для оценки параметров которых используются вероятностные характеристики при от- сутствии некоторых данных об объекте (моделирование това- рооборота в условиях вероятности поставок товаров). Областью использования моделей являются: обучение, на- учные исследования, управление. По признаку полноты моделирование: полное; неполное; приближенное. Полное моделирование обеспечивает построение модели, которая идентична объекту изучения как во времени, так и в пространстве. При неполном моделировании идентичность модели и объ- екта нарушается. При приближенном моделировании некоторые стороны реального объекта совсем не моделируются. Модели экономического процесса могут классифицировать- ся в соответствии со следующими признаками: 1. Целевое предназначение модели: исследовательские (по- лучение количественных характеристик и установление зако- номерностей); органов управления (для принятия решения, пла- нирования, организации деятельности, контроля и др.); модели, используемые в составе автоматизированных информационных систем управления технологическими процессами. 2. Способ представления оригинала: натурно-теоретические; натурные; теоретические: мысленные (логические); математи- ческие (аналитические; статистические); смешанные логико- графические; графоматематические (графоаналитические, графостатистические); графические; комбинированные. 3. Вид моделируемого процесса (в соответствии с этим при- знаком): стратегические; оперативные; тактические. 4. Характер описываемого процесса: детерминированные; вероятностные. 5. Характер протекания описываемого процесса: непрерыв- ные; для прогнозирования скачков. 6. Вид описания процесса: аналитические; имитационные. 7. Способ использования и обмена информации: индивиду- ального использования; коллективного использования (исполь- зования в составе обучающих систем); использование в составе локальных или глобальных компьютерных сетей. 8. Способ ввода информации: из банка данных; баз данных; импорт из других моделей и систем. 9. Способ вывода результирующей информации и ее ис- пользования: выработка управляющего воздействия; система параметров (данных). 10. Возможность корректирования структуры в ходе ее экс- плуатации: корректируемые; некорректируемые. 364 365 Словесно-описательные — комплекс слов, характеризую- щих поведение изучаемого явления или объекта, правила по- ведения человека в различных жизненных ситуациях. Приме- рами словесно-описательных моделей могут быть технические задания, пояснительные записки, обзоры коньюктуры рынка и конкурентов, общая характеристика магазина. Словесно- описательные модели позволяют достаточно полно на качествен- ном уровне описывать объект управления. Пример. Приведем словесно-описательную модель сервис- ной организации. Сервисная организация существует в пространстве и во вре- мени в правовой и законодательной среде общества в сочетании с потребностями своих сотрудников, существующих и будущих кли- ентов при соблюдении закона сохранения ресурсов: финансовых, людских, материальных, духовных, моральных и этических. Математические модели — совокупность математических средств, отображающих функциональные зависимости элемен- тов объекта изучения. Математические модели подразделяются на детермини- рованные (определенные) и стохастические (вероятностные или неопределенные). Детерминированные (определенные) модели характерны тем, что результат решения задачи полностью предопределяется заданным набором исходных данных. Стохастические (вероятностные или неопределенные) модели описывают такие процессы, для оценки параметров которых используются вероятностные характеристики при от- сутствии некоторых данных об объекте (моделирование това- рооборота в условиях вероятности поставок товаров). Областью использования моделей являются: обучение, на- учные исследования, управление. По признаку полноты моделирование: полное; неполное; приближенное. Полное моделирование обеспечивает построение модели, которая идентична объекту изучения как во времени, так и в пространстве. При неполном моделировании идентичность модели и объ- екта нарушается. При приближенном моделировании некоторые стороны реального объекта совсем не моделируются. Модели экономического процесса могут классифицировать- ся в соответствии со следующими признаками: 1. Целевое предназначение модели: исследовательские (по- лучение количественных характеристик и установление зако- номерностей); органов управления (для принятия решения, пла- нирования, организации деятельности, контроля и др.); модели, используемые в составе автоматизированных информационных систем управления технологическими процессами. 2. Способ представления оригинала: натурно-теоретические; натурные; теоретические: мысленные (логические); математи- ческие (аналитические; статистические); смешанные логико- графические; графоматематические (графоаналитические, графостатистические); графические; комбинированные. 3. Вид моделируемого процесса (в соответствии с этим при- знаком): стратегические; оперативные; тактические. 4. Характер описываемого процесса: детерминированные; вероятностные. 5. Характер протекания описываемого процесса: непрерыв- ные; для прогнозирования скачков. 6. Вид описания процесса: аналитические; имитационные. 7. Способ использования и обмена информации: индивиду- ального использования; коллективного использования (исполь- зования в составе обучающих систем); использование в составе локальных или глобальных компьютерных сетей. 8. Способ ввода информации: из банка данных; баз данных; импорт из других моделей и систем. 9. Способ вывода результирующей информации и ее ис- пользования: выработка управляющего воздействия; система параметров (данных). 10. Возможность корректирования структуры в ходе ее экс- плуатации: корректируемые; некорректируемые.

К моделям экономических систем предъявляются следую- щие требования: 1. Адекватность представления процесса (модель должна правильно отражать основные факторы и величины). 2. Блочно-модульный принцип построения модели (поэтап- ное моделирование позволяет осуществить реконструкцию моделей без существенного изменения структуры). 3. Разумное сочетание необходимой полноты с простотой использования расчетов (они противоречивы). 4. Чувствительность модели к изменению параметров управ- ляющих процессов функционирования системы. 5. Высокая мобильность и оперативность проведения ис- следования либо подготовки предложений для принятия управ- ляющих решений. 6. Документирование входной и выходной информации (го- товый текст решения). 7. Оптимальная обработка информации, поступающей от различных источников, с целью достижения высокой точности исходных данных, используемых непосредственно для моде- лирования. 8. Возможность обеспечение активной коррекции своей струк- туры по результатам фактической информации о ходе процесса. 9. Структурное построение модели должно обеспечивать ее эксплуатацию как автономно, так и в составе автоматизирован- ных информационных систем. 10. Малая стоимость

Аналитические модели экономических систем, построенные на основе зависимостей, полученных по результатам обработки ретроспективной информации показателей их функционирования, и основанные на описании процессов с помощью дифференциальных уравнений. (смотри в методичке Сист.анализ стр.415)

43. Основные понятия и определения имитационного моделирования. Время и пространство в имитационных моделях. Этапы разработки имитационных моделей. Планирование и проведение экспериментов в имитационных моделях. (см. в метод. Систем.анализ стр.453, 459. http://www.rae.ru/fs/?section=content&op=show_article&article_id=7981766)

Имитация в переводе с латинского означает отображение. Имитационная модель — аналог какого-либо процесса или явления, созданный путем отображения. Моделирование — процесс разработки модели или процесс получения каких-либо характеристик, например экономических, с помощью модели. Имитационное моделирование — процесс разработки имитационной модели или процесс получения каких либо характеристик, например экономических с помощью имитационной модели. Имитационный эксперимент — эксперимент, проведенный с помощью имитационной модели.

Время и пространство в имитационных моделях Основными составляющими имитационного процесса явля- ются: время, пространство, функциональное действие, актив- ность, поведение. 1. Всякий реальный процесс, в том числе и экономический, представляется в виде совокупности функциональных действии (ФД). В основу функционального действия могут быть положе- ны: достижение какой либо-цели или же подцели; выполнение (решение) задачи, при которой достигается цель или подцель; реализация какой-либо функции; выполнение работы или мероприятия; наступление какого-либо события; реализация процесса или явления. Функциональные действия в реальной системе могут осуществляться последовательно, параллельно, последовательно-параллельно. 2. Всякое функциональное действие начинается и заканчи- вается в определенные моменты времени tнi и tкi и имеет определенную продолжительность ti. 3. Все функциональные действия описываются неким алгоритмом. 4. Пары (алгоритм и текущее время или функциональное действие и текущее время) в теории имитационного моделиро- вания называют активностью. Любая активность представляет 460 461 собой запись поведения имитационной модели, приводящей к появлению интересующего нас события. Момент начала функ- ционального действия в теории принято называть инициали- зацией. 5. Функциональным действием в экономических моделях может быть перемещение компонента во времени и про- странстве, реализация мероприятия или выполнение работ. В результате этой деятельности наступает интересующее нас событие. Учет времени в имитационных моделях экономического процесса При реализации имитационных моделей экономического процесса обычно используют четыре представления времени: 1. Реальное время работы системы, которая имитируется на данной модели tр. 2. Глобальное модельное время, по которому организуется синхронизация событий в системе в целом tмг. 3. Локальное модельное время, по нему осуществляется син- хронизация отдельных функциональных деятельностиtмл. 4. Машинное время имитации, отражающее затраты ре- сурса времени ЭВМ на организацию имитации t. Существуют два способа имитации модельного времени (tмг и tмл): • способ фиксированного шага Dt = const; • способ переменного шага Dt = varia. Могут возникнуть неудобства от того, что при постоянном шаге можно “проскочить” интересующее нас событие. Пере- менный шаг зависит от текущего времени. В ходе моделиро- вания оценивается время до события и выбирается шаг, чтобы его не “проскочить”. Зависимость функционального действия от времени опре- деляется поведением системы, которое задается исходными данными моделируемого процесса либо формируется в ходе моделирования в итоге наступления тех или иных событий. На- пример, при наступлении события “Цель достигнута”, процесс моделирования завершается. В имитационной модели реализуется как будто бы парал- лельный процесс (так как однопроцессорная ЭВМ решает задачи последовательно). Существуют следующие основные способы организации квазипараллелизма: просмотр активностей; составление рас- писаний событий; транзактный способ; агрегатный способ; про- цессный способ; комбинированный способ. Просмотр активностей. Условие применимости: — все функциональные действия компонент Кi реальной системы различны; — для выполнения каждого функциональные действия требуется выполнение своих условий; — условия выполнения каждого функциональные действия могут быть представлены алгоритмически; — связи между функциональными действиями отсутствуют. Алгоритм реализации способа 1. Осуществляется просмотр всех функциональных дей- ствия. Параметр цикла равен максимальному числу активно- стей. 2. Имена активностей, для которых выполняются условия, заносятся в список инициализируемых. Далее начинается цикл по числу инициализируемых активностей (цикл просмотра деятельности). 3. Определяется интересующее нас событие. Алгоритм организации квазипараллелизма просмотром активностей приведен на рис. 3.24. Составление расписаний событий. Условия применимости: — различные компоненты моделируемой системы выпол- няют одни и те же функциональные действия; — начало выполнения функциональные действия опреде- ляется одними и теми же условиями; — в результате выполнения одних и тех же функциональ- ных действий в системе происходят одинаковые события неза- висимо друг от друга. 460 461 собой запись поведения имитационной модели, приводящей к появлению интересующего нас события. Момент начала функ- ционального действия в теории принято называть инициали- зацией. 5. Функциональным действием в экономических моде- лях может быть перемещение компонента во времени и про- странстве, реализация мероприятия или выполнение работ. В результате этой деятельности наступает интересующее нас событие. Учет времени в имитационных моделях экономического процесса При реализации имитационных моделей экономического процесса обычно используют четыре представления времени: 1. Реальное время работы системы, которая имитируется на данной модели tр. 2. Глобальное модельное время, по которому организуется синхронизация событий в системе в целом tмг. 3. Локальное модельное время, по нему осуществляется син- хронизация отдельных функциональных деятельностиtмл. 4. Машинное время имитации, отражающее затраты ре- сурса времени ЭВМ на организацию имитации t. Существуют два способа имитации модельного времени (tмг и tмл): • способ фиксированного шага Dt = const; • способ переменного шага Dt = varia. Могут возникнуть неудобства от того, что при постоянном шаге можно “проскочить” интересующее нас событие. Пере- менный шаг зависит от текущего времени. В ходе моделиро- вания оценивается время до события и выбирается шаг, чтобы его не “проскочить”. Зависимость функционального действия от времени опре- деляется поведением системы, которое задается исходными данными моделируемого процесса либо формируется в ходе моделирования в итоге наступления тех или иных событий. На- пример, при наступлении события “Цель достигнута”, процесс моделирования завершается. В имитационной модели реализуется как будто бы парал- лельный процесс (так как однопроцессорная ЭВМ решает задачи последовательно). Существуют следующие основные способы организации квазипараллелизма: просмотр активностей; составление рас- писаний событий; транзактный способ; агрегатный способ; про- цессный способ; комбинированный способ.

Основные понятия оптимизации и классификация методов решения оптимизационных задач. Постановка задачи и общий порядок разработки оптимизационной модели экономической системы. (см. в методичке сист. Анализ стр. 605 и 611).

Поиск оптимального решения — нахождение таких усло- вий организации системы (процесса), при которых достигается экстремум некоторой функции или функционала. Примерами оптимизационных задач могут выступать: • выбор дороги из дома на работу таким образом, чтобы за- тратить меньше времени и выполнить определенные условия; • определение неизвестных параметров модели, обеспечи- вающих минимальное отклонение выходных координат, полу- ченных экспериментальным путем, от рассчитанных по модели. Это задача идентификации;

• выгодное проведение финансовой сделки, обеспечивающей максимальную прибыль при выполнении определенных балан- совых соотношений и т. д. При решении задач оптимизации используются следующие понятия. Критерий оптимальности — величина, оценивающая каче- ство искомого решения. Примерами экономических критериев могут выступать себестоимость, прибыль. Целевая функция — функция, позволяющая рассчитать числовое значение критерия оптимальности. Иногда значение критерия оптимальности определяется функционалом, т. е. не- кой интегральной функцией. Переменная оптимизации — переменная, определяемая при решении оптимизационной задачи. Решение оптимизационной задачи обычно находится при некоторых условиях. Они могут быть двух типов: определяться условиями в форме неравенств — это ограничения, определяться равенствами — это связи. Ограничения могут быть автономные — накладываются на каждую переменную оптимизации в отдельности, и неавтоном- ные — накладываются на совокупность переменных. Связи обычно задаются алгебраическими уравнениями, дифференциальными, интегральными и т. д. и являются урав- нениями математической модели. Для решения задачи оптимизации формальными методами необходимо формализовать постановку задачи. Формализация постановки задачи включает в себя несколько этапов: • словесная (содержательная) постановка; • введение обозначений; • формализация условий задачи. Значение найденных переменных оптимизации, при кото- рых достигается экстремум критерия оптимальности (на области допустимых значений), называется решением оптимизационной задачи. Значение целевой функции при соответствующем ей зна- чении критерия называют значением задачи. 608 609 Задача оптимизации считается корректно поставленной, если она имеет решение, решение это единственное и устой- чивое. В противном случае задача считается некорректно по- ставленной. Если в задаче оптимизации используется одновременно несколько критериев оптимальности, то такая задача многокри- териальная. Например, необходимо одновременное сокращение расходов на сырье при увеличении количества выпускаемой продукции и повышение прибыли от ее реализации. Эффективных методов решения многокритериальных задач нет, и решение таких задач часто не единственное. Можно привести несколько методов решения многокрите- риальных задач: • Нахождение решения, оптимального по Парето. Множе- ство решений называется оптимальным по Парето, если ни одно из этих решений нельзя улучшить ни по одному из критериев, не ухудшая одновременно значение другого критерия. • Метод справедливого компромисса, когда ухудшение по одному из критериев приравнивается к улучшению другого критерия. • Метод уступок, когда все критерии упорядочиваются по важности и задача решается итеративно. • Метод свертки критериев, когда переходят или к взве- шенной сумме (произведению) всех критериев со своими весо- выми коэффициентами (при этом все критерии нормируются и приводятся к одной размерности), или к однокритериальной задаче, выбирая один наиболее важный критерий и учитывая остальные в ограничениях. Все методы оптимизации, позволяющие находить решение оптимизационных задач, можно классифицировать по разным признакам: 1. В зависимости от наложения условий: • методы безусловной оптимизации (когда на переменные оптимизации не накладываются какие-либо условия); • методы условной оптимизации (когда требуется соблю- дение определенных условий). 2. В зависимости от числа переменных оптимизации: • методы одномерной оптимизации (одна переменная оптимизации); • методы многомерной оптимизации (целевая функция зависит от нескольких переменных оптимизации). 3. В зависимости от вида функции, определяющей условия задачи: • методы линейного программирования, если все функции, определяющие условия задачи, линейны; • методы нелинейного программирования, если функции, определяющие условия задачи, нелинейные; • методы дискретного программирования, если хотя бы часть переменных оптимизации может принимать только дис- кретные значения; • методы вариационного исчисления, если хотя бы часть переменных оптимизации или величин, зависящих от них, яв- ляются функциями времени или пространственной координаты. Критерием оптимальности в таких задачах является всегда функционал, например интеграл. Методами безусловной оптимизации функции одной пере- менной (одномерного поиска) являются, например, методы: • сканирования; • дихотомии; • золотого сечения, • фибоначи. Методами безусловной оптимизации функции нескольких переменных (многомерного поиска) являются, например, методы: • градиентные: — с постоянным шагом; — с оптимальным шагом (наискорейшего спуска или подъ- ема); — ускоренный. • безградиентные: — метод Гаусса-Зейделя (покоординатный подъем с по- стоянным или оптимальным шагом); — симплексный метод (деформированного многогранника); 608 609 Задача оптимизации считается корректно поставленной, если она имеет решение, решение это единственное и устой- чивое. В противном случае задача считается некорректно по- ставленной. Если в задаче оптимизации используется одновременно несколько критериев оптимальности, то такая задача многокри- териальная. Например, необходимо одновременное сокращение расходов на сырье при увеличении количества выпускаемой продукции и повышение прибыли от ее реализации. Эффективных методов решения многокритериальных задач нет, и решение таких задач часто не единственное. Можно привести несколько методов решения многокрите- риальных задач: • Нахождение решения, оптимального по Парето. Множе- ство решений называется оптимальным по Парето, если ни одно из этих решений нельзя улучшить ни по одному из критериев, не ухудшая одновременно значение другого критерия. • Метод справедливого компромисса, когда ухудшение по одному из критериев приравнивается к улучшению другого критерия. • Метод уступок, когда все критерии упорядочиваются по важности и задача решается итеративно. • Метод свертки критериев, когда переходят или к взве- шенной сумме (произведению) всех критериев со своими весо- выми коэффициентами (при этом все критерии нормируются и приводятся к одной размерности), или к однокритериальной задаче, выбирая один наиболее важный критерий и учитывая остальные в ограничениях. Все методы оптимизации, позволяющие находить решение оптимизационных задач, можно классифицировать по разным признакам: 1. В зависимости от наложения условий: • методы безусловной оптимизации (когда на переменные оптимизации не накладываются какие-либо условия); • методы условной оптимизации (когда требуется соблю- дение определенных условий). 2. В зависимости от числа переменных оптимизации: • методы одномерной оптимизации (одна переменная оптимизации); • методы многомерной оптимизации (целевая функция зависит от нескольких переменных оптимизации). 3. В зависимости от вида функции, определяющей условия задачи: • методы линейного программирования, если все функции, определяющие условия задачи, линейны; • методы нелинейного программирования, если функции, определяющие условия задачи, нелинейные; • методы дискретного программирования, если хотя бы часть переменных оптимизации может принимать только дис- кретные значения; • методы вариационного исчисления, если хотя бы часть переменных оптимизации или величин, зависящих от них, яв- ляются функциями времени или пространственной координаты. Критерием оптимальности в таких задачах является всегда функционал, например интеграл. Методами безусловной оптимизации функции одной пере- менной (одномерного поиска) являются, например, методы: • сканирования; • дихотомии; • золотого сечения, • фибоначи. Методами безусловной оптимизации функции нескольких переменных (многомерного поиска) являются, например, методы: • градиентные: — с постоянным шагом; — с оптимальным шагом (наискорейшего спуска или подъ- ема); — ускоренный. • безградиентные: — метод Гаусса-Зейделя (покоординатный подъем с по- стоянным или оптимальным шагом); — симплексный метод (деформированного многогранника); 610 611 — метод случайного поиска; — метод параллельных касательных. Методами условной оптимизации функции нескольких переменных являются: • метод неопределенных множителей Лагранжа; • метод штрафных функций. Этот метод осуществляет переход от задачи условной оптимизации к задаче безусловной оптимизации, когда к целевой функции добавляется в виде до- полнительного слагаемого функция штрафа за невыполнение связей и ограничений. Задачи линейного программирования, которые наиболее часто встречаются в экономике, решаются с использованием симплекс-метода. (Не путать с симплексным методом, методом деформированного многогранника, методом многомерных не- линейных задач безусловной оптимизации). При решении вариационных задач может использоваться принцип максимума Понтрягина. При решении оптимизационных задач управления многоста- дийными процессами (задачи дискретного программирования) (например, задача сетевого планирования, задача коммивояже- ра) используются методы динамического программирования на основе принципа Беллмана. Метод решения задачи выбирается в зависимости от клас- сификации поставленной оптимизационной задачи. Решение задачи может сочетать в себе разные методы.

Сетевая модель системы. Расчет параметров сетевой модели. Современные информационные технологии разработки и применения сетевых моделей экономических систем. (см. методичку Сист. Анализ 433, 437, 444).

Date: 2015-08-15; view: 1894; Нарушение авторских прав