Понятие о локсодромии и ортодромии

При движении судна постоянным истинным курсом линия курса пересекает каждый меридиан под одним и тем же углом и на земной поверхности эта линия получается двоякой кривизны, называемая локсодромией (что в переводе с греческого означает «косой бег»).

Плавание по локсодромии удобно, так как курс судна остается постоянным, а это упрощает все расчеты, связанные с прокладкой. Основные свойства локсодромии, проходящей через две точки, можно выявить из ее уравнения:

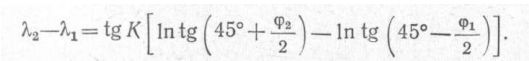
Из этого уравнения следует, что при К = 0° или К = 180° tg К = 0, тогда и λ2 — λ1 = 0, следовательно, на истинных курсах 0 или 180° долгота точек не изменяется и локсодромия совпадает с меридианом, превращаясь в дугу большого круга, и в данном случае проходит через земные полюса.

Если уравнение написать в виде

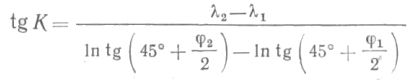
и принять К — 90° или К = 270°, то при этих значениях tg К = ~. Так как разность долгот λ2 — λ1 находящаяся в числителе, не может быть равна бесконечности, то должен быть равен нулю знаменатель, а он может быть равен нулю при 45° + φ1/2 = 45°+ φ2/2 т. е. когда φ1 = φ2.

Рис. 36

Следовательно, при К = = 90° или К = 270° широта точек не изменяется и локсодромия совпадает с параллелью или при φ2 = φ1 = = 0 — с экватором.

Для всех истинных курсов, отличных от 0 — 180° и 90 — 270°, локсодромия по спирали приближается к одному из полюсов, но никогда его не достигает (рис. 36).

Длина отрезка локсодромии, пройденного судном на данном курсе, не является кратчайшим расстоянием на земной поверхности. Кратчайшим расстоянием на земной поверхности при переходе судна из одной точки до другой будет дуга большого круга, называемая ортодромией (что в переводе с греческого означает «прямой бег»).

Ортодромия с каждым меридианом составляет переменные углы. Поэтому плавание по ортодромии требует предварительного вычисления как ее положения, так и курсов, которыми ведут судно по дуге большого круга (см. § 46).

Date: 2015-08-15; view: 769; Нарушение авторских прав