Уравнения равновесия Лагранжа

По определению (7) обобщенные силы 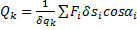, k = 1,2,3,…, s, где s – число степеней свободы.

Если система находится в равновесии, то по принципу возможных перемещений (1) . Здесь 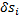– перемещения, допускаемые связями, возможные перемещения. Поэтому при равновесии материальной системы все ее обобщенные силы равны нулю:

Q_k = 0, (k =1,2,3,…, s). (10)

Эти уравнения, уравнения равновесия в обобщенных координатах или уравнения равновесия Лагранжа, позволяют решать задачи статики еще одним методом.

Если система консервативная, то 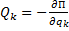. Значит, в положении равновесия 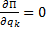. То есть в положении равновесия такой материальной системы ее потенциальная энергия либо максимальна, либо минимальна, т.е. функция П(q) имеет экстремум.

Это очевидно из анализа простейшего примера (рис.11). Потенциальная энергия шарика в положении М ₁ имеет минимум, в положении М ₂ – максимум. Можно заметить, что в положении М ₁ равновесие будет устойчивым; в положении М ₂ – неустойчивым.

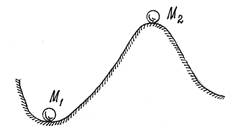
Рис.11

Равновесие считается устойчивым, если телу в этом положении сообщить малую скорость или сместить на малое расстояние и эти отклонения в дальнейшем не увеличатся.

Можно доказать (теорема Лагранжа-Дирихле), что если в положении равновесия консервативной системы ее потенциальная энергия имеет минимум, то это положение равновесия устойчиво.

Для консервативной системы с одной степенью свободы условие минимума потенциальной энергии, а значит и устойчивости положения равновесия, определяется, второй производной, ее значением в положении равновесия,

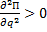. (11)

Пример 5. Стержень ОА весом Р может вращаться в вертикальной плоскости вокруг оси О (рис.12). Найдем и исследуем устойчивость положений равновесия.

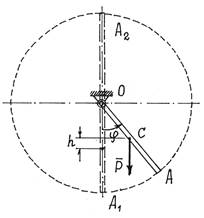
Рис.12

Решение. Стержень имеет одну степень свободы. Обобщенная координата – угол .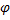

Относительно нижнего, нулевого, положения потенциальная энергия П= Рh или

В положении равновесия должно быть 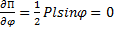. Отсюда имеем два положения равновесия, соответствующие углам 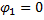и (положения ОА ₁ и ОА ₂). Исследуем их устойчивость. Находим вторую производную 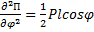. Конечно, при , . Положение равновесия устойчиво. При , 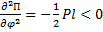. Второе положение равновесия – неустойчиво. Результаты очевидны.

Date: 2015-08-15; view: 620; Нарушение авторских прав