Обобщенные координаты

Обобщенными координатами мы будем называть параметры, которые определяют положение материальной системы.

Это могут быть обычные декартовы координаты точек, углы поворота, расстояния, площади, объемы и т.д.

Так на рис.7 положение балочки АВ и всех ее точек вполне определяется углом .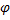

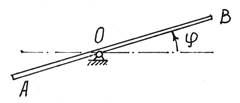
Рис.7

Положение точек кривошипно-шатунного механизма (рис.8) можно определить заданием угла поворота 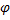кривошипа или расстоянием s, определяющим положение ползуна В (при ).

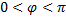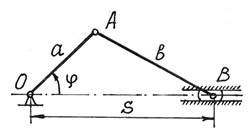
Рис.8

Положение сферического маятника (рис.9) определяется заданием двух параметров, углов и .

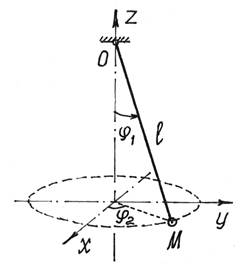
Рис.9

Минимальное количество независимых друг от друга обобщенных координат, которых достаточно, чтобы полностью и однозначно определить положение всех точек системы, называют числом степеней свободы этой системы.

Вообще для любой материальной системы можно назначить несколько обобщенных координат. Например, у кривошипно-шатунного механизма (рис.8) указаны две обобщенные координаты 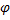и s. Но это не значит, что у механизма две степени свободы, так как одну координату можно определить через другую:

.

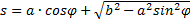А вот у маятника (рис.71) две степени свободы, т.к. определяется его положение двумя независимыми обобщенными координатами. Кстати, если длина маятника изменяется, то для определения положения точки М потребуется еще один параметр – обобщенная координата l, длина нити. И у маятника станут три степени свободы.

Обобщенные координаты в общем случае будем обозначать буквой q.

Пусть материальная система имеет s степеней свободы. Положение ее определяется обобщенными координатами: q ₁, q ₂, q ₃,…, q_k,…, q_{s. .}

Нетрудно убедиться, что декартовы координаты n точек системы можно определить как функции обобщенных координат и времени:

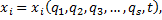
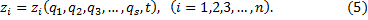
Так у маятника (рис.9) координаты точки М

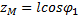
есть функции координат l, и , и времени t, если l = l(t).

Соответственно, и радиус-вектор точек системы можно определить как функцию обобщенных координат и времени:

(6)

Date: 2015-08-15; view: 475; Нарушение авторских прав