Методы измерения световых величин. Объективные и субъективные фотометры

Раздел оптики, занимающийся измерениями световых величин, называется фотометрией. Приборы, приспособленные для измере­ния силы света или световых потоков разных источников, назы­ваются фотометрами. По принципу регистрации фотометры бывают двух типов: субъективные (визуальные) и объективные.

Субъективные фотометры. В основе субъективных фотометров лежит зрительное наблюдение. Оно основано на том, что ощущение яркости является монотонной функцией энергии падающего света. Следовательно, если два различных источника света, одинаковых по спектральному составу, вызывают в глазу одинаковые ощущения яркости, то они посылают в глаз одинаковые энергии. Этот факт лежит в основе так называемых визуальных фотометров равной яркости. В фотометрах равной яркости две граничащие площадки освещаются каждая отдельным источником. Изменяя расстояние до одного из источников, добиваются одинаковой освещенности прилегающих друг к другу полей. В этом случае каждый из источ­ников посылает на единицу поверхности освещаемого им поля одинаковый поток энергии. Исходя из этого, с помощью визуаль­ных фотометров можно определить силу света некоторого источ­ника в данном направлении, если известна сила света, принятого в качестве эталона другого источника. Аналогичным образом можно определить световой поток, посланный источником в разных напра­влениях, а следовательно, и полный световой поток источника.

Во избежание дополнительных искажений полученных резуль­татов площадки фотометра освещаются под одними и теми же углами. То же самое относится и к углам наблюдения этих сравни­ваемых площадей.

С целью определения полного светового потока применяется так называемый сферический фотометр. Для достижения одинаковой освещенности сравниваемых площадок с помощью двух разных источников пользуются разными приборами и применяются разные методы. Выбор того или иного метода обусловливается конкретной постановкой задачи.

Использование закона обратных квадратов. Коротко остановимся на некоторых методах определения фотометрических величин. В основе самого простого метода определения силы света лежит закон обратной пропорциональности освещённости квадрату расстояния между точечным источником и освещаемой им поверхностью.

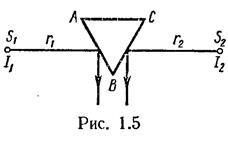
Источники света с силами I ₁и I ₂, расположены от освещаемых поверхностей А В и ВС соответственно на рас­стояниях r ₁и r ₂ (рис. 1.5). Освещенности соответствующих по­верхностей при освещении под одними и теми же углами будут

и 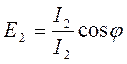. (1.21)

Варьируя r ₁и r ₂, можно добиться Е ₁ = Е ₂. Тогда имеем

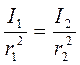, отсюда . (1.21)

Определив r ₁и r ₂ при известном I ₂, можно вычислить I ₁.

При использовании этого метода следует принять во внимание, что закон обратных квадратов применим для точечных источников. Кроме того, этот метод практически менее выгоден при сравнении источников, мощности которых резко отличаются, так как в этом случае r ₁и r ₂ будут также сильно отличаться друг от друга.

Использование ослабителей освещения.

Как мы видели, сущ­ность метода определения силы света сводится к выравниванию осве­щенности поверхностей, освещаемыми источниками разной силы света. Следовательно, разные методы будут отличаться друг от друга способами ослабления освещенности, создаваемой более силь­ными источниками. В одном из методов измерения применяются ослабители переменной толщины (рис. 1.6).

Клинообразные ослабители способны скользить но соприкасаю­щимся поверхностям друг относительно друга. При этом меняется толщина области, через которую проходит излучение от более силь­ного источника. Достигнув нужной толщины, где происходит по­глощение, можно добиться необходимой освещенности рассматриваемой поверхности. Очевидно, что применяемые ослабители должны быть нейтральны к белому свету, т, е, они должны в одинаковой степени поглощать свет различной длины волны. К ослаблению освещенности приводит так­же использование на пути светового пучка вращающегося диска с векториальным вырезом (при вращении диска непрозрачная часть, периодически закрывая путь свету, ослабляет его интенсивность).

Схематическое изображение самого простого визуального фото­метра представлено на рис. 1.5.

Фотометр Люммера-Бродхуна.

Более совершенным визуальным фотометром является фотометр Люммера-Бродхуна (рис. 1.7). Он состоит из кубика Люммера (Р ₁ Р₂), зеркал S₁ и S₂ экрана S, диффузно рас­сеивающего свет, и лупы Л. Кубик Люммера-Бродхуна (рис. 1.8) состоит из ивух прямоугольных призм. Соприка­сающаяся поверхность одной из призм «выполнена так, чтобы средняя часть ее находилась в полном оптическом контакте со второй призмой, другими сло­вами, соприкасающиеся части призм ведут себя как однородное тело. По этой причине лучи, исходящие от источни­ка L ₁ пройдя через центральную контактную часть призм, попадают в приемник. Лучи, исходящие из источника L ₂, направляются так, чтобы они падали на внутреннюю поверхность первой призмы Р ₁ Р ₂под углами, большими 45° (предельный угол на границе воздух — стекло составляет 45°). При удовлетворении этого условия лучи, падающие на неконтактирующую часть поверхности первой призмы, претерпев полное внутреннее отражение, попадут в приемник. Таким образом, наблюдатель увидит пло­щадку, центральная часть которой освещена источником L ₁,a края — источником L ₂.

Освещенности центральной части и края наблюдаемой картины будут одинаковыми (исчезает граница раздела между ними), если обе поверхности экрана S будут освещены одинаково. По достиже­нии такой одинаковой освещенности можно вычислить отношение силы света источников L ₁ и L ₂, измерив расстояния L ₁ S и L ₂ S.

Объективные фотометры. В объективных фотометрах в основе определения фотометрических величин лежат электрические и фо­тографические методы.

В фотографическом методе исходят из того, что степень почер­нения фотопластинки пропорциональна количеству падающей на нее световой энергии.

Принцип работы электрофотометра основан на электрическом действии света (фотоэлементы, фотоусилители, фотосопротивления и т. д.). Самый простой фотоэлектрический фотометр состоит из фотоэлемента и соединенного с ним высокочувствительного гальва­нометра. Если измерить электроток, создаваемый действием света, то можно вычислить освещенность поверхности фотометра. Проградуировав гальванометр непосредственно в люксах, можно получить величину освещенности. В качестве фотоусилителей могут быть использованы так называемые фотоэлектронные усилители (ФЭУ). Выбор того или иного ФЭУ обусловлен спектральным составом изме­ряемого светового потока. Так, например, для красной и близкой инфракрасной областей спектра применяются фотоусилители ФЭУ-62, ФЭУ-22. Для сине-зеленой области применимы ФЭУ-17, ФЭУ-18, ФЭУ-19 и т. д. ФЭУ-18, ФЭУ-39 рассчитаны на работу в ультрафиолетовой и сине-зеленой областях спектра. ФЭУ-106 применяется как в видимой, так и в ультрафиолетовой и инфра­красной областях спектра.

Объективные фотометры свободны от многих недостатков, при­сущих визуальным фотометрам. Преимуществом объективного фото­метра является возможность его использования также в невидимой части спектра (в ультрафиолетовой и инфракрасной), что приводит к более широкому их применению по сравнению с субъективными фотометрами.

Лабораторная Работа № 2

Определение фокусного расстояния сферической линзы

Вопросы для теоретической подготовки:

1. Преломление и отражение на сферической поверхности (вывод нулевого инварианта Аббе). Как получить из формулы преломления на сферической поверхности, формулу сферического зеркала и формулу тонкой линзы?

Предположим, что две среды с показателями преломления п ₁и n ₂ разделяются сферической поверхностью Σ (рис. 2.1). На ли­нии LL', проходящей через центр нашей сферы О, поместим точечный источник света L.

Рассмотрим узкий гомоцентрический конус лучей, падающий из L на поверх­ность раздела двух сред.

Мы предполагаем пучок настолько узким, т. е. угол ψ настолько малым, что практически можно считать отрезок LS равным LA, L'S равным L'A и т. д. Такой узкий пучок будем называть параксиальным (приосевым).

Итак, условие параксиальности пучка есть LS≈LA и L'S≈L'A.

Возьмем какой-либо луч из этого пучка, например LA, падающий на Σ под углом i, построим сопряженный ему преломленный луч AL' (угол преломления r) и найдем положение точки, в которой преломленный луч пересечет ось системы. Из треугольника ALO имеем

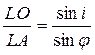
из треугольника OAL'

Отсюда

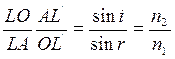(2.1)

В дальнейшем все отрезки вдоль оси будем отсчитывать от точки S, считая положительными отрезки, откладываемые от S вправо (в направлении распространяющегося света), и отрицательными — отрезки, откладываемые влево. Таким образом, AL ≈ SL = - а ₁, AL^’≈SL^’ = a ₂, AO = SO = R (радиус сферы). В таком случае LO = - a ₁ + R, OL^’ = a ₂ – R.

,

т. е.

(2.2)

Последняя формула показывает, что произведение 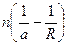при преломлении сохраняет свою величину Q. Его называют нулевым инвариантом Аббе. Для многих целей этой формуле удобно придать вид

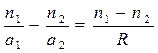(2.3)

Соотношение (2.3) позволяет найти длину а₂ = SL', если за­дано а ₁= LS, т. е. позволяет отыскать положение точки L' по за­данному L. При выводе его мы, кроме закона преломления, поль­зовались еще допущением, что луч LA принадлежит к параксиаль­ному пучку. Следовательно, соотношение справедливо для любого луча параксиального пучка. Из формулы (2.3) видно, что а₂ при заданных параметрах задачи (n₁,n₂,R) зависит только от а ₁.Таким образом, все лучи параксиального гомоцентрического пучка, выходящего из L. Итак, гомоцентрический пучок при преломлении на сферической поверхности остаётся гомоцентрическим, если он удовлетворяет условию параксиальности. Основное уравнение (2.3) охватывает все случаи преломления лучей на сферической поверхности. Пользуясь установленным выше правилом знаков, мы можем разобрать случай выпуклой (R > 0) или вогнутой (R < 0) поверхности.

Из основного уравнения (2.3)

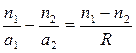
следует, что при а _{1 =} -∞

, (2.4)

при а ₂ = ∞

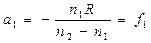, (2.5)

т. е. f 1, f ₂ зависят только от радиуса кривизны поверхности R и по­казателей преломления n _l, п ₂обеих сред.

Величины f ₁ и f ₂ постоянные длины, характеризующие преломляющую поверхность. Они называются ее фокусными расстояниями: f ₁— переднее фокусное расстояние (точка F ₁— пе­редний фокус); f ₂— заднее фокусное расстояние (точка F₂ — задний фокус) (рис. 2.2).

Таким образом, фокусом сферической поверхности называется точка, в которой сходятся после преломления параллельные лучи (т. е. лучи, идущие из бесконечно удаленной точки). Понятно, что фокусы, так же как и изображения, могут быть действительными и мнимыми, т. е. представлять точку пересечения преломленных лучей (бывших до преломления параллельными) или их предполагаемых продолжений.

В качестве примера рассмотрим сферическое зеркало. Формулу (2.3) можно применить и к случаю отражения, если положить n₂ = -n₁. Тогда имеем

1/a₁+1/a₂=2/R, (2.5)

т. е. известную формулу сферического зеркала. Фокусное расстоя­ние такого зеркала определится по формуле (2.1). Найдем f = R/2, и, следовательно, формуле зеркала можно придать вид

1/a₁+1/a₂ = 1/ f. (2.6)

В случае зеркала изображение действительное, если оно лежит по одну сторону с источником, и мнимое, если расположено за зеркалом.

Случаи вогнутого и выпуклого зеркала отличаются лишь знаком R. Легко видеть, что фокус вогнутого зеркала - действительный, а фокус выпуклого зеркала - мнимый.

Чтобы получить законы плоского зеркала, достаточно положить R = ∞. В этом случае найдем a ₁= -а₂, т.е. изображение точки в плоском зеркале мнимое и симметрично расположенное.

Вывод формулы тонкой линзы. Выведем формулу тонкой линзы, исходя из формулы сферической поверхности. Показатель прелом­ления материала линзы обозначим через п. Показатели преломления сред справа и слева от линзы обозначим соответственно через п ₁и n₂. Построим изображение точки М, лежащей на главной оптичес­кой оси на расстоянии а₁от линзы. Построение изображения точки М на тонкой линзе произведем следующим образом: построим сперва изображение точки на одной поверхности, затем, рассматривая это изображение как источник, построим его изображение на второй поверхности. Будем пользоваться правилом, согласно которому лучи, идущие параллельно данной оптической оси, после прелом­ления в линзе пересекутся в одной точке, лежащей на фокальной плоскости. Соответствующее построение показывает, что изображе­ние точки М на первой сферической поверхности, разграничивающей среды с показателями преломления слева п ₁и справа n₂, нахо­дится на расстоянии М ₁A= а от этой поверхности, Тогда, согласно формуле сферической (для первой поверхности в нашем случае) поверхности, имеем

n ₁ /a ₁ - n/a = (n₁ - n)/R₁. ( 2.7 )

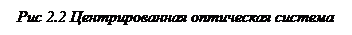
Как мы условились, построим теперь изображение точки M₁ на второй преломляющей поверхности, разграничивающей среды с показате­лями преломления слева - п, справа - п ₂. Этим изображением явля­ется точка М₂, расположенная на расстоянии а ₂от этой поверхности. В этом случае имеем

п/а - п ₂ /а ₂= (n - n ₂ )/R ₂. ( 2.8 )

Так как обычно линза с обеих сторон охватывается одинаковой сре­дой, то п ₁= п ₂. Тогда, складывая (7.12) и (7.13), получим

1 /a₂ - 1 /a₁ = (N - 1 ) ( 1 /R ₁ - 1 /R ₂ ), ( 2.9 )

где N = n/n₁ - показатель преломления материала линзы отно­сительно окружающей среды (относительный показатель прелом­ления). Формула (2.9) является формулой тонкой линзы и верна как для выпуклых, так и для вогнутых линз при произвольном расположении точки М. При a₁ = - ∞ получим

(2.10)

При a₂ = ∞ имеем

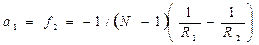(2.11)

Как видно, f i = - f ₂, т.е. фокусные расстояния линзы, окруженной с обеих сторон одинаковой средой, равны. Знак минус показывает, что фокусы расположены по разные стороны от линзы.

Исходя из выражений (2.9) и (2.11), формулу линзы можно -написать в более простом виде:

1/ a ₂ – 1/ a ₁ = 1/ f ₁. (2.12)

Применяя эту формулу для разных случаев, можно получить из нее конкретные результаты. При работе с формулами (2.9) и (2.12) не следует забывать, что величины справа от линзы положительные, слева - ­ отрицательные.

Тонкая сферическая линза. Главная оптическая ось, главный фокус, оптический центр линзы. Построение изображений предмета, расположенного между фокусом и линзой, между фокусом и двойным фокусным расстоянием и дальше двойного фокусного расстояния в собирающей и рассеивающей линзах.

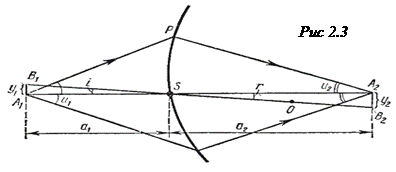
Теорема Лагранжа - Гельмгольца. В предыдущем параграфе мы построили изображение светящейся точки S₁ на оси с помощью одной сферической преломляющей поверхности. Построим теперь изображение не точки, а светящегося малого отрезка А ₁ В ₁перпен­дикулярного продолжению оси OS (рис. 2.3). Построение изобра­жения будем производить параксиальным пучком света. В случае параксиальных лучей тангенсы углов и ₁и и ₂, определяющие макси­мальное раскрытие (апертуру) соответственно падающих на прелом­ляющую поверхность и сопряженных им изображающих пучков, можно заменить значениями самих углов.

Выясним, в каких соотношениях находятся предмет и его изобра­жение, если построение производится параксиальным пучком.

Обозначим показатели преломления сред соответственно слева и справа от преломляющей поверхности через п ₁и п ₂, длину отрезка - через y ₁, длину изображения - через у ₂, расстояния от A ₁ B ₁ и А ₂ В ₂до преломляющей поверхности -соответственно через a ₁ и а₂, углы падения и преломления - через i и r. Из Δ A ₁ B ₁ S и Δ A ₂ B ₂ S соответственно имеем:

tg i = y ₁/a₁, tg r = y ₂/ a _2.

Ввиду малости длин у ₁и у ₂тангенсы углов падения и преломле­ния можно заменить синусами соответствующих углов. Принимая во внимание также закон преломления света, получим

tg i /tg r = sin i /sin r = (y ₁/a₁) (а ₂ /у ₂ ) = n ₂ ln ₁ (2.13)

и прямо пропорционально отношению показателей преломления первой среды ко второй.

Соответственные точки предмета и изображения, в которых γ = 1, называются узловыми. Плоскости, проходящие через узлы перпендикулярно оптической оси, называются узловыми плоско­стями. Как следует из выражения углового увеличения при п ₁= п ₂, если поверхность с обеих сторон окружена одной и той же средой, оно равно 1/β. Следовательно, если сферическая поверхность расположена в однородной среде, то главная плоскость совпадает с узловой плоскостью, а главная точка — с угловой.

Центрированная оптическая система. Оптические системы обычно состоят из двух и более преломляющих поверхностей. Представляет интерес случай, когда центры всех поверхностей, входящих в состав оптической системы, лежат на одной прямой (рис. 2.4). Оптическая система, обладающая этим свойством, называется центрированной.

Прямая линия, на которой расположены центры всех поверхностей системы, называется главной оптической осью. Центрированная оптическая система обладает свойством сохранять гомоцентричность параксиального пучка, т.е. в центрированной оптической системе гомоцентрический параксиальный пучок остается гомоцен­трическим независимо от числа преломляющих (или отражающих) поверхностей. В этом легко убедиться,если произвести построение параксиальными пучками, причем изобра­жение от каждой предыдущей поверх­ности считать предметом для после­дующей.

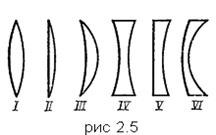
Линза. Самой простой центрированной оптической системой является линза. Она состоит из двух поверх­ностей, ограничивающих прозрачный (обычно стекло) материал, одна из которых обязательно является сферической, а другая может быть сферической или плоской. В зависимости от вида ограничивающих поверхностей линзы бывают двояковыпуклыми, плосковыпуклыми, двояковогнутыми, плосковогнутыми и вогнуто-выпуклыми (рис. 2.5). Легко убе­диться, что линзы /, //, /// являются собирательными, а лин­зы IV, V, VI - рассеивающими, если их материал оптически

плотнее, чем окружающая среда. В противоположном случае линзы /, //, /// являются рассеивающими, а линзы IV, V, VI -собирательными.

Тонкая двояковыпуклая линза. Рассмотрим двояковыпуклую линзу (рис.2.6). Линза называется тонкой, если толщина ее достаточно мала по сравнению с радиусами кривизны R ₁и R ₂ограни­чивающих поверхностей, чтобы обе ее вершины А и В можно было считать практически совпадающими. Точка слияния А и В назы­вается центром линзы (обозначим ее через С). Любая прямая линия, проведенная через центр линзы, называется оптической осью линзы. Оптическая ось, проведенная через центры О₁ и О₂, назы­вается главной.

Центральную часть тонкой линзы можно принять за плоско­параллельную пластинку. Следовательно, лучи, проходящие через центр линзы, практически не преломляются.

Построение изображений в тонкой линзе. Все вышеизложенное позволяет легко определить ход лучей, необходимых для построения изображения в тонкой линзе:

1) луч, падающий параллельно оптической оси линзы, после преломления пересекает данную ось по другую сторону линзы в точ­ке, расположенной на расстоянии f от нее;

2) луч, падающий на линзу и проходящий через ее фокус, вы­ходит из линзы параллельно ее оптической оси;

3) луч, проходящий через оптический центр линзы, не изменяет своего направления,

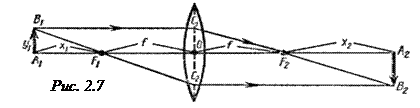
Выше мы построили изображение точки в тонкой линзе, распо­ложенной на ее главной оптической оси. Построим теперь изображе­ние отрезка A ₁ B ₁ длиной у ₁(рис. 2.7) в тонкой линзе. Для этого достаточно построить изображение точки B ₁. При построении будем пользоваться лучами, направления которых после прелом­ления в линзе известны. Изображением отрезка А ₁ В ₁ в линзе будет отрезок длиной А ₂ В ₂. Расстояния предмета и его изображения от фокусов F ₁ и F₂ соответственно обозначим через х ₁и х ₂. Отношение β = = y ₂ /y ₁называется линейным увеличением линзы. Отрицательным значениям β соответствует действительное, а положительным - мнимое изображение.

Точки пересечения фокальных плоскостей с главной оптичес­кой осью называются фокальными точками, или главными фокусами оптической системы. Главный фокус пространства предметов (пе­редний главный фокус) будем обозначать через F, а главный фокус пространства изображений (задний главный фокус) - через F'.

Date: 2015-08-07; view: 3017; Нарушение авторских прав