Удельная теплоёмкость

Удельной теплоёмкостью называется теплоёмкость, отнесённая к единичному количеству вещества. Количество вещества может быть измерено в килограммах, кубических метрах и молях. В зависимости от того, к какой количественной единице относится теплоёмкость, различают массовую, объёмную и молярную теплоёмкость.

Массовая теплоёмкость (С) — это количество теплоты, которое необходимо подвести к единице массы вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на килограмм на кельвин (Дж·кг−1·К−1).

Объёмная теплоёмкость (С′) — это количество теплоты, которое необходимо подвести к единице объёма вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на кубический метр на кельвин (Дж·м−3·К−1).

Молярная теплоёмкость (Сμ) — это количество теплоты, которое необходимо подвести к 1 молю вещества, чтобы нагреть его на единицу температуры. В СИ измеряется в джоулях на моль на кельвин (Дж/(моль·К)).

Существует несколько теорий теплоёмкости твердого тела:

Закон Дюлонга — Пти и закон Джоуля — Коппа. Оба закона выведены из классических представлений и с определенной точностью справедливы лишь для нормальных температур (примерно от 15 °C до 100 °C).

Квантовая теория теплоёмкостей Эйнштейна. Первое применение квантовых законов к описанию теплоёмкости.

Квантовая теория теплоёмкостей Дебая. Содержит наиболее полное описание и хорошо согласуется с экспериментом.

Теплоёмкость системы невзаимодействующих частиц (например, газа) определяется числом степеней свободы частиц.

Единица измерения теплоёмкости в системе СИ — Дж/К.

Второе начало термодинамики. Второе начало термодинамики задает направленность процессов, протекающих в изолированной термодинамической системе. Оно гласит:

изменение энтропии изолированной системы всегда положительно dS > 0 или равно нулю в случае достижения энтропией своего максимального значения.

Другими словами энтропия изолированной системы не может убывать.

Состояние с максимальным значением энтропии является равновесным. Еще раз отметим, что данная формулировка имеет статистический смысл, т.е. возможны некоторые отрицательные флуктуации изменения энтропии в отдельные моменты времени.

Второе начало термодинамики — физический принцип, накладывающий ограничение на направление процессов передачи тепла между телами.

Второе начало термодинамики гласит, что невозможен самопроизвольный переход тепла от тела, менее нагретого, к телу, более нагретому.

Второе начало термодинамики запрещает так называемые вечные двигатели второго рода, показывая что коэффициент полезного действия не может равняться единице, поскольку для кругового процесса температура холодильника не может равняться абсолютному нулю.

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

Для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния 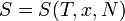, называемая энтропией, такая, что ее полный дифференциал.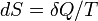

Определение энтропии и ее свойства. Величина, являющаяся функцией состояния, должна обладать свойством аддитивности. Действительно, макросистему всегда можно разбить на части и при этом функция состояния всей системы должна равняться сумме функций состояния ее частей.

Термодинамическая вероятность таким свойством не обладает. Покажем это на примере. Разобьем некую макросистему на две подсистемы, обладающие термодинамическими вероятностями W1 и W2. Число способов реализации данного состояния системы как единого целого для независимых событий равно произведению W = W1·W2.

Из курса математики известно, что логарифм произведения равен произведению логарифмов. Следовательно, логарифм термодинамической вероятности таким свойством обладает свойством аддитивности, т.е.

lnW = lnW1 + lnW2.

Величина, равная произведению постоянной Больцмана на логарифм термодинамической вероятности, называется энтропией S.

S = k·lnW. (15.3)

Свойства энтропии:

энтропия является аддитивной величиной;

энтропия - есть функция состояния макросистемы;

энтропия изолированной системы при протекании необратимых процессов возрастает;

энтропия макросистемы, находящейся в равновесном состоянии, максимальна.

Date: 2015-08-07; view: 472; Нарушение авторских прав