Свойства индуктивности

Правило Ленца

Ленца правило, определяет направление индукционных токов, т. е. токов, возникающих вследствие индукции электромагнитной; является следствием закона сохранения энергии. Л. П. установлено в 1833 Э. X. Ленцем. Согласно Л. п., возникающий в замкнутом контуре индукционный ток направлен так, что создаваемый им поток магнитной индукции через площадь, ограниченную контуром, стремится препятствовать тому изменению потока, которое вызывает данный ток. Так, например, индукционный ток в витке, помещенном в магнитное поле В, которое направлено перпендикулярно плоскости витка (рис.) от наблюдателя (т. е. за плоскость чертежа), направлен против часовой стрелки, если поле возрастает во времени (а), и по часовой стрелке, если поле убывает (б).

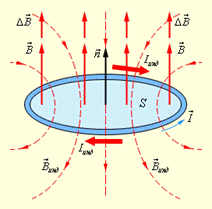суть правила Ленца

Индуктивность, коэффициент самоиндукции (L)—отношение потокосцепления самоиндукции цепи к силе тока в ней. Характеризует связь потокосцепления самоиндукции с силой тока контура. Измеряется в генри (Г). Индуктивность кольцевой катушки L=μaW2S/l, где W — количество витков; S — поперечное сечение катушки; l — длина катушки; μa — магнитная проницаемость среды.

Свойства индуктивности

Индуктивность всегда положительна.

Индуктивность зависит только от геометрических размеров контура и магнитных свойств среды (сердечника).

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность[1], краем которой является этот контур.[2][3][4].

В формуле 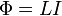,где Ф- магнитный поток,L-индуктивность, I-ток в контуре

Уравнения Максвелла представляют собой в векторной записи систему из четырёх уравнений, сводящуюся в компонентном представлении к восьми (два векторных уравнения содержат по три компоненты каждое плюс два скалярных[28]) линейных дифференциальных уравнений в частных производных первого порядка для 12 компонент четырёх векторных функций: D,E,H,B,D

E — напряжённость электрического поля (в единицах СИ — В/м);

H — напряжённость магнитного поля (в единицах СИ — А/м);

D — электрическая индукция (в единицах СИ — Кл/м²);

B — магнитная индукция (в единицах СИ — Тл = Вб/м² = кг•с−2•А−1);

В дифференциальной форме:

Первое М. у. имеет вид:

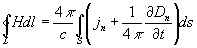
то есть циркуляция вектора напряжённости магнитного поля вдоль замкнутого контура L (сумма скалярных произведений вектора Н в данной точке контура на бесконечно малый отрезок dl контура) определяется полным током через произвольную поверхность S, ограниченную данным контуром. Здесь jn — проекция плотности тока проводимости j на нормаль к бесконечно малой площадке ds, являющейся частью поверхности S, с = 3․1010 см/сек — постоянная, равная скорости распространения электромагнитных взаимодействий в вакууме.

Второе М. у. является математической формулировкой закона электромагнитной индукции Фарадея (см. Индукция электромагнитная) записывается в виде:

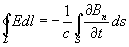
то есть циркуляция вектора напряжённости электрического поля вдоль замкнутого контура L (эдс индукции) определяется скоростью изменения потока вектора магнитной индукции через поверхность S, ограниченную данным контуром. Здесь Bn — проекция на нормаль к площадке ds вектора магнитной индукции В; знак минус соответствует Ленца правилу (См. Ленца правило) для направления индукционного тока.

Третье М. у. выражает опытные данные об отсутствии магнитных зарядов, аналогичных электрическим (магнитное поле порождается только токами):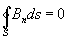

то есть поток вектора магнитной индукции через произвольную замкнутую поверхность S равен нулю.

Четвёртое М. у. (обычно называемое Гаусса теоремой (См. Гаусса теорема)) представляет собой обобщение закона взаимодействия неподвижных электрических зарядов — Кулона закона:

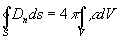
то есть поток вектора электрической индукции через произвольную замкнутую поверхность S определяется электрическим зарядом, находящимся внутри этой поверхности (в объёме V, ограниченном данной поверхностью).

М. у. в форме (1) или (2) не образуют полной замкнутой системы, позволяющей рассчитывать электромагнитные процессы при наличии материальной среды. Необходимо их дополнить соотношениями, связывающими векторы Е, Н, D, В и j, которые не являются независимыми. Связь между этими векторами определяется свойствами среды и её состоянием, причём D и j выражаются через Е, а B — через Н:

D = D (E), B = B (Н), j = j (E). (3)

Эти три уравнения называются уравнениями состояния, или материальными уравнениями; они описывают электромагнитные свойства среды и для каждой конкретной среды имеют определённую форму. В вакууме D ≡ Е и B ≡ Н. Совокупность уравнений поля (2) и уравнений состояния (3) образуют полную систему уравнений.

Электромагнитная волна - процесс распространения электромагнитного поля в пространстве.

Электромагнитная волна представляет собой процесс последовательного, взаимосвязанного изменения векторов напряжённости электрического и магнитного полей, направленных перпендикулярно лучу распространения волны, при котором изменение электрического поля вызывает изменения магнитного поля, которые, в свою очередь, вызывают изменения электрического поля.

Date: 2015-08-07; view: 340; Нарушение авторских прав