Исчисление предикатов как аксиоматическая система

ИП - аксиоматическая система, построенная согласно формальной теории F = (A, V, W, R).

Словарь ИП (A) содержит:

индивидные константы a, b, c...;

предметные переменные x, y, z,...;

функциональные константы f, g, h..;

высказывания p, q, r, s,....;

предикатные константы P, Q, R,...

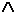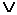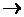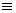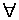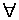Исчисление предикатов, в определенном смысле, продолжение и расширение исчисления высказываний, поэтому в словарь включены все те же пропозициональные связки , , НЕ, , . Но перечень логических знаков в ИП расширяется еще двумя, называемых кванторами: и . Квантор читается как "все", "для всех", "всякий", "каков бы ни был" и т.п. Поэтому он называется квантором всеобщности (общности). Квантор читается как "некоторый", "хотя бы один", "существует" и т.п.. Поэтому он называется квантором существования. Так, например, выражение 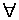xP(x) читается: "для любого x выполняется условие P (x)". Выражение yP (y) - "существует хотя бы один y, при котором выполняется P (y) (т.е. Р(у) = И)".

Множество синтаксических правил V ИВ применимо и в ИП. Правильно построенные формулы в рамках исчисления высказываний остаются ппф и в исчислении предикатов. Добавляются правила:

атом есть формула и

если Р (х) формула и х - переменная, то 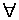хР (х) и хР (х) - формулы.

Каждому квантору соответствует только одна переменная, в наших примерах x или y. Эта переменная называется квантифицированной, она пишется сразу за квантором. Область действия квантора - формула, к которой применяется эта квантификация. Каждое вхождение квантифицированной переменной в область действия квантификации является связанным, любая другая переменная в данной области, не являющаяся связанной, называется свободной.

Рассмотрим формулу 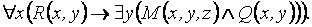Здесь все вхождения переменной x связанные, т.к. попадают в область действия квантора 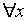, которая включает в себя все предикаты: R,M и Q (следите за скобками). А вот первое вхождение переменной y (в предикате R) - свободное. В дальнейшем y попадает в область квантификации 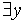и является связанным (в предикатах M и Q). Переменная z - свободная.

Каждую предикатную формулу можно интерпретировать, т.е. оценить ее как И или Л. При этом можно оценить "перекрытие" кванторов на одну и ту же переменную:

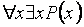интерпретируется как 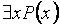, а

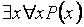интерпретируется как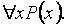

Это и понятно: вместо того, чтобы говорить " из всех х существует хотя бы один х, при котором Р истинен", достаточно сказать просто: "существует хотя бы один х и т.д.". И наоборот, чтобы не говорить странное словосочетание "существует хотя бы один х, такой, что для всех х Р истинен", достаточно сказать "для всех х...". (Для запоминания: из двух кванторов "прав" самый правый).

Будем понимать под А предикат A (x,y) и отметим важные соотношения:

,

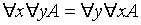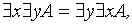(6.1)

т.е. одноименные кванторы можно менять местами. Иное дело разноименные кванторы. Здесь выполняется только такое условие:

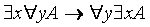. (6.2)

Последняя импликация поясняется следующим примером. Пусть имеем для целых чисел истинное утверждение: 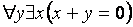(для любого y найдется такой х, что выполняется равенство 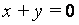). Переставим кванторы: 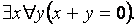Получим выражение: существует такой х, при котором выполняется условие ( 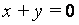) для всех y, что некорректно.

Система базовых аксиом W в ИП может быть принята такой же, как и в ИВ. Однако к ней необходимо добавить аксиомы, учитывающие появление кванторов:

(A4) ,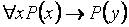

(A5) .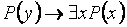

A4 говорит, что если P (x) истинен для всех х, то он истинен и для некоторого y из этого же универсума (если все яблоки в данном ящике красные, то одно-то красное уж найдется всегда).

А5 говорит, что если найдется y, при котором P (y) истинен, то верно, что найдется хотя бы один x, для которого предикат P (x) тоже истинен (даже если x совпадает с y). (Если среди яблок в данном ящике нашлось одно сладкое, то уже существует по крайней мере одно сладкое).

Правила вывода R здесь остаются прежними: правило подстановки и правило заключения, но они дополняются еще одним правилом, учитывающим свойства кванторов. Это правило называется правилом специализации. Суть его в следующем: если ппф 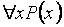истинна и b - некоторая константа, то формула P(b) также истинна, т.е. справедливо 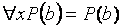. Пусть, например, имеются формулы 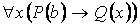и P (b). Если они истинны, то, применяя специализацию, имеем ряд теорем:

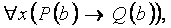
т.е. 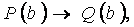(специализация)

Q (b) (modus ponens с P (b)).

Date: 2015-08-06; view: 721; Нарушение авторских прав