
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

С. С. Вечканов, Н. Н. Клочкова, А. Н. Проценко
|
|
МОДЕЛЬ ЭНЕРГОЭФФЕКТИВНОГО ИНДУКТОРА ПОПЕРЕЧНОГО МАГНИТНОГО ПОЛЯ
С.С.Вечканов, Н.Н.Клочкова, А.Н.Проценко.
МП ЭСО г.о.Самары
Россия, 443110, г.Самара, ул.Искровская,7
Самарский государственный технический университет
Россия, 443100, г. Самара, ул. Молодогвардейская, 244
В работе разрабатывается и исследуется модель энергоэффективного индуктора поперечного магнитного поля на примере технологической операции нагрева цилиндрической алюминиевой заготовки. Предлагается конструкция индуктора, с замкнутым цилиндрическим магнитопроводом в форме статора трехфазного асинхронного двигателя. Показаны преимущества такой конструкции относительно соленоидальных многосекционных индукторов, с точки зрения равномерности загрузки фаз питающей сети. Исследовалась зависимость коэффициента полезного действия индукционной установки от ширины витка индуктора. Определены параметры конструкции, дающие наибольший коэффициент полезного действия. Решена задача нагрева алюминиевой цилиндрической заготовки до требуемой температуры с допустимым перепадом температуры от поверхности до центра.
Ключевые слова: поперечное магнитное поле, система индукционного нагрева, технологическая операция, замкнутый цилиндрический магнитопровод, заготовка, трехфазная система, несимметрия, энергоэффективный индуктор.
Статья посвящена разработке и исследованию модели системы индукционного нагрева в поперечном магнитном поле.
Практически во всех отраслях промышленности применяются индукционные системы для преобразования электромагнитной энергии в тепловую. Опыт показывает, что они являются перспективными по ряду важнейших признаков. Они надежны, безопасны, компактны и позволяют осуществлять автоматическое управление процессом нагрева.
Мощные индукционные нагревательные установки представляют собой многосекционную систему индукторов и не обеспечивают симметричную нагрузку фаз даже при полном равенстве собственных сопротивлений отдельных секций трехфазного нагревателя. Это приводит к ухудшению качества электроэнергии в системе электроснабжения даже при симметричной питающей трехфазной системе. Устранить или уменьшить это можно при помощи специальных симметрирующих устройств, применение которых может оказаться нецелесообразным, так как мощность индукционных нагревателей в процессе нагрева может существенно изменяться. В этом случае необходимо применять регулируемые симметрирующие устройства, что значительно удорожает стоимость нагревательной установки. Поэтому в настоящее время возникает необходимость поиска путей совершенствования имеющихся конструкций и принципов работы установок индукционного нагрева [1, 2]. Одним из вариантов такого подхода может быть конструкция индуктора, с замкнутым цилиндрическим магнитопроводом в форме статора трехфазного асинхронного двигателя (рис.1).
В трехфазной обмотке индуктора сопротивления фаз в цепи статора симметричны, так как все фазы имеют одинаковое число витков. Сопротивления нагрузки (заготовки), также можно считать симметричными. источник питания, в качестве которого может рассматриваться трехфазный трансформатор, предполагается симметричным, с соответствующим сдвигом по фазам. Поэтому можно утверждать, что в нормальном режиме несимметрия отсутствует полностью. Однако, реализация предлагаемой конструкции нагревателя требует решения определенных задач [4, 5]. В общем случае, процесс индукционного нагрева цилиндрической заготовки в индукторе с замкнутым магнитопроводом описывается нелинейной взаимосвязанной системой уравнений Максвелла и Фурье. Соответственно для электромагнитного и теплового полей с соответствующими краевыми условиями:
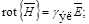
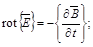
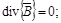
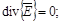
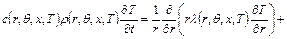
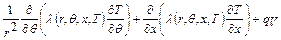
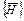 ,
, 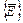 ,
, 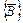 - векторы напряженности магнитного и электрического полей и магнитной индукции,
- векторы напряженности магнитного и электрического полей и магнитной индукции, 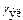 - удельная электропроводимость, T – температура, t – время,
- удельная электропроводимость, T – температура, t – время, 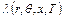 - компоненты тензора теплопроводности (теплопроводность как функция температуры представляется кубическим сплайном),
- компоненты тензора теплопроводности (теплопроводность как функция температуры представляется кубическим сплайном), 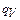 - удельная мощность тепловыделения (в линейной постановке - константа, в нелинейной постановке - задаваемая кубическим сплайном в функции температуры),
- удельная мощность тепловыделения (в линейной постановке - константа, в нелинейной постановке - задаваемая кубическим сплайном в функции температуры), 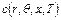 - удельная теплоемкость (в нелинейном случае это функция температуры, аппроксимированная кубическими сплайнами),
- удельная теплоемкость (в нелинейном случае это функция температуры, аппроксимированная кубическими сплайнами), 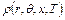 - плотность,
- плотность, 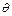 - угловая координата. Система уравнений для электромагнитного поля дополняется граничными условиями: используются условия равенства функции нулю на бесконечно удаленной границе
- угловая координата. Система уравнений для электромагнитного поля дополняется граничными условиями: используются условия равенства функции нулю на бесконечно удаленной границе 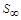 и условие симметрии на поверхности симметрии
и условие симметрии на поверхности симметрии 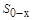 , которое заключается в равенстве нулю производной от функции. Для тепловой задачи используется более широкий спектр граничных условий – от условия симметрии (граничные условия второго рода) до теплообмена между соприкасающимися телами (граничное условие четвертого рода). При описании процессов нагрева наиболее адекватной является электротепловая модель, основанная на численном решении уравнений электромагнетизма и теплопроводности. Такие модели учитывают взаимное влияние электромагнитного и температурного полей в процессе индукционного нагрева и дают исчерпывающую характеристику индукционного устройства с точки зрения потребления энергии от внешнего источника питания и выделения ее в загрузке. Связь электромагнитного поля в системе с температурным полем обусловлена зависимостью удельного сопротивления и магнитной проницаемости от температуры, что обусловливает характер распределения внутренних источников тепла.
, которое заключается в равенстве нулю производной от функции. Для тепловой задачи используется более широкий спектр граничных условий – от условия симметрии (граничные условия второго рода) до теплообмена между соприкасающимися телами (граничное условие четвертого рода). При описании процессов нагрева наиболее адекватной является электротепловая модель, основанная на численном решении уравнений электромагнетизма и теплопроводности. Такие модели учитывают взаимное влияние электромагнитного и температурного полей в процессе индукционного нагрева и дают исчерпывающую характеристику индукционного устройства с точки зрения потребления энергии от внешнего источника питания и выделения ее в загрузке. Связь электромагнитного поля в системе с температурным полем обусловлена зависимостью удельного сопротивления и магнитной проницаемости от температуры, что обусловливает характер распределения внутренних источников тепла.
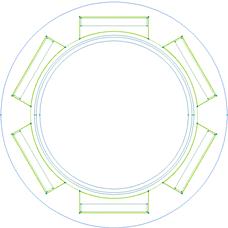
Рис. 1. Конструкция предлагаемой установки
индукционного нагрева
Одна из первоочередных задач – разработка модели энергоэффективного индуктора поперечного магнитного поля.
Цилиндрическую заготовку из алюминия (диаметр – 420мм, магнитная проницаемость – 1, электропроводность – 25650000 см/мм), необходимо нагреть до температуры 753К, при этом перепад температуры от края до центра заготовки не должен превышать 25К. За управляющие параметры принимаются ширина паза и плотность тока. За искомые параметры принимаются – КПД и перепад температуры в от края до центра заготовки.
Геометрическая модель конструкции создается в программе Elcut 5.1 pro, где имеется возможность задавать свойства различных материалов и граничные условия. После описания физических свойств всех компонентов геометрической модели и назначения граничных условий, формируется математическая модель. Модель состоит из 3 модулей: задача стационарной теплопередачи (нелинейная), задача вихревых токов и задаче нестационарной теплопередачи (нелинейная). Задача стационарной теплопередачи описывает начальное температурное распределение. Задача вихревых токов описывает стационарный электромагнитный процесс в заготовке, а задача нестационарной теплопередачи на основе результатов связанных с ней двух предыдущих задач описывает изменение распределения температуры в заготовке. Передача данных в программе осуществляется с помощью связи задач, когда задача нестационарной теплопередачи решается на основе результатов решений задачи стационарной теплопередачи и задачи вихревых токов. Модули решаются последовательно.
 На рисунке 1 изображен эскиз двухмерной геометрической модели системы индукционного нагрева с помещенной в нее алюминиевой заготовкой. На рисунке 2 обозначены области системы индукционного нагрева.
На рисунке 1 изображен эскиз двухмерной геометрической модели системы индукционного нагрева с помещенной в нее алюминиевой заготовкой. На рисунке 2 обозначены области системы индукционного нагрева.








Рис. 2. Часть геометрической модели с 1 витком.
На геометрической модели присутствует 6 одинаковых витков, равномерно распределенных по окружности.
Определим ширину витка индуктора, обеспечивающую наибольший КПД индукционной системы. Для этого меняем ширину паза от 40 до 200мм. При этом плотность тока удерживается постоянная и равная 18.5 А/мм2, исходя из предельного значения плотности тока для меди. Изменяемый диапазон ширины витка лежит в зоне насыщения и далек от зон действия высших гармоник. Рисунок 3 показывает изменение КПД в окрестности экстремума в увеличенном масштабе. На отрезке 165-195 мм различия КПД составляют 0.3% при погрешности вычислений 0.013% [3].
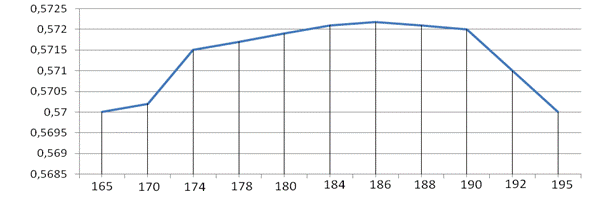
Рис. 3. Изменение КПД в зависимости от ширины паза в окрестности экстремального значения.
Из графика следует, что максимальную величину КПД обеспечивает паз шириной 186 мм. Но при этом перепад температуры от поверхности до центра заготовки составляет 173К, что не соответствует требованиям нагрева. Теперь необходимо добиться перепада температуры от поверхности до центра заготовки не более 25К. Для этого будем уменьшать плотность тока в проводнике, не изменяя ширину паза для сохранения максимальной величины КПД. После серии вычислительных экспериментов было установлено, что требуемый перепад температуры достигается при плотности тока 7.32 А/мм2 и ширине паза 186 мм. Рисунок 3 показывает, что наибольший КПД индуктора сохраняется при той же ширине паза, что и в предыдущей задаче. Погрешность КПД составляет 0.013% [3].
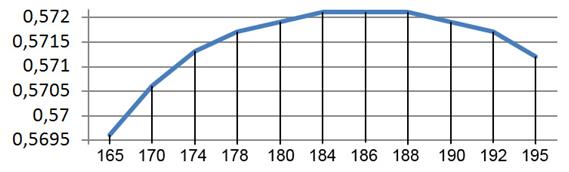
Рис. 4. Изменение КПД в зависимости от ширины паза в окрестности экстремального значения.
В ходе проведенных исследований были определены параметры конструкции: индукционная система с индуктором, состоящим из 6 продольных витков, шириной 186 мм, уложенных в пазы магнитопровода под углом 60 градусов относительно друг друга.. При ширине паза 186мм, плотности тока 7.32 А/мм2 перепад температуры в заготовке 25 К, КПД индуктора 57.21%.
Date: 2015-08-06; view: 402; Нарушение авторских прав