Выполненные контрольные работы студент представляет в деканат заочного факультета. Лабораторные работы студент непосредственно сдает своему преподавателю

8. Если контрольная работа при рецензировании не зачтена, студент обязан представить ее на повторную рецензию, включив в нее те задачи, решения которых оказались неверными. Повторную работу необходимо представить вместе с незачтенной.

Вариант №1 Приложение 1

1. 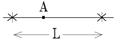Два точечных когерентных источника радиоволн расположены на расстоянии L = 24 м друг от друга и испускают монохроматическую волну с λ = 5 м. В точке А на линии, соединяющей источники, наблюдается интерференционный максимум. На каком минимальном расстоянии от любого из источников волн может находиться точка А?

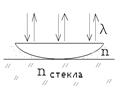
2. В отраженном вертикально вверх свете наблюдается радужное пятно разлитой бензиновой пленки. Какой может быть минимальная толщина этой пленки в месте, где видна красная полоска (l_k = 800 нм)? Пленка разлита на горизонтальной стеклянной пластинке. Показатели преломления бензина n_б = 1,6, стекла – n_c = 1,8.

3. 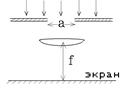Плоская монохроматическая волна с длиной волны λ падает нормально на узкую щель ширины a = 7λ. За щелью нормально к падающей волне расположена линза, собирающая все лучи, выходящие из щели, на экране, расположенном в ее фокальной плоскости. Фокусное расстояние линзы f = м. Чему равно отношение ширины изображения щели на экране (расстояние между первыми дифракционными минимумами по обе стороны от главного максимума освещенности) к фокусному расстоянию f? Длина волны λ сравнима с величиной f.

4. 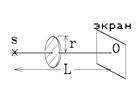Точечный источник света S находится на расстоянии SO = L = 0,5 м от экрана. Посередине этого расстояния между источником и экраном ставят круглую непрозрачную преграду радиусом r = 0,25 мм ось которой совпадает с линией SO. Освещенность в точке О при этом увеличивается в 4 раза (максимальна). Какова длина волны l света, испускаемого источником?

5. Работа выхода электрона из цезия равна 1,8 эВ. Чему равен минимальный импульс фотона (в кг×м/с), способного выбить из цезия электрон с кинетической энергией 2,7 эВ? с = 3×10⁸ м/с.

6. Испускательная способность некоторого равномерно нагретого тела в форме шара зависит от длины волны испускаемых электромагнитных волн по закону r(λ) = Aexp(-αl), где А = 6×10^–3 Вт/м³, α = 1,2×10^–7 м^–1 - постоянные. Какую мощность излучает это тело, если площадь его поверхности равна S = 0,03 м²?

7. Во сколько раз длина волны де Бройля свободного электрона, движущегося со скоростью 2×10⁶ м/с, больше длины волны де Бройля электрона, движущегося в атоме водорода по стационарной орбите с радиусом 5,3×10^–11 м (основное состояние атома водорода)? Масса электрона m = 9,1×10^–31 кг, 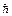= 1,06106×10^–34 Дж×с.

8. Микрочастица, описываемая волновой функцией ψ = Asin(αx), где А = const, α = 8×10¹⁰ м^–1, имеет кинетическую энергию К = 5 эВ. Полагая 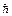= 10^–34 Дж×с, найти массу m микрочастицы.

9. Тонкий пучок атомов водорода в основном состоянии влетает в неоднородное магнитное поле с постоянным градиентом индукции |grad B| = 40 Тл/м. Вектор grad B направлен перпендикулярно оси пучка и за время t = 10^–4 с пролета в магнитном поле каждый из атомов отклоняется от оси пучка на расстояние Δx. Найти это отклонение Δx, если масса атома m_н = 1,68×10^–27 кг; магнетон Бора m_Б = 9,24×10^–24 А×м².

10. Используя нерелятивистское выражение v = 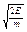, найти среднюю величину <v> скорости свободных электронов из зоны проводимости в металле с уровнем Ферми Е_ф = 3,2 эВ при Т = 0 К. Масса электрона m = 9×10^–31 кг.

11. Полупроводник с шириной запрещенной зоны 0,72675 эВ нагревают от 300 К до 323 К. Во сколько раз увеличится при этом собственная проводимость полупроводника? k = 1,38×10^–23 Дж/К.

12. Распад радиоактивного элемента с постоянной распада λ = 0,06 с^–1 наблюдают в течении времени Δt. После первой половины этого промежутка времени нераспавшихся атомов было в k раз больше, чем в конце промежутка Δt, где ln k = 1,5. Найти величину Δt времени наблюдения.

Вариант №2

1. Два точечных источника испускают радиоволны с длиной волны λ= 40 м в одной фазе. На каком минимальном расстоянии друг от друга надо расположить эти источники, чтобы волны практически не излучались вдоль одного из направлений.

2. 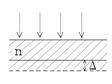Белый свет, отраженный вертикально от горизонтально расположенной в воздухе плоской стеклянной пластинки, оказывается окрашен в красный свет (l_k = 660 нм). Если постепенно увеличивать толщину пластинки, то отраженные лучи снова окажутся окрашенными в тот же красный свет, когда эта толщина увеличится на Δ = 220 нм. Чему равен показатель преломления стекла n?

3. 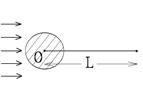На узкую щель ширины a = 0,5 мм падает нормально плоская монохроматическая волна (длина волны равна λ = 500 нм). На большом расстоянии b = 5 м за щелью стоит параллельный ей экран. Какова ширина изображения щели (расстояние между первыми дифракционными минимумами по обе стороны от главного максимума освещенности) на экране?

4. Плоская монохроматическая радиоволна с λ = 4,8 м падает на сферический металлический спутник. При каком минимальном радиусе спутника интенсивность радиоизлучения на оси симметрии спутника на расстоянии L = 30 м от его центра О в области создаваемой им "тени" будет максимальна?

5. Фотон падает на металл с работой выхода А = 2,1 эВ и выбивает электрон. Чему равна энергия фотона (в эВ), если при падении на металл с вдвое большей работой выхода А' он выбьет электрон, улетающий с вдвое меньшей скоростью?

6. В нагретом сосуде, стенки которого можно считать абсолютно черным телом, находится равновесное тепловое излучение при температуре Т = 1000 К. Средняя частота фотона в этом излучении равна <ν> = 3,8×10¹⁵ Гц. Сколько фотонов будет вылетать из сосуда за 1 секунду через крошечное отверстие с площадью S = 4,4×10^–8 м²? Принять h = 6,6×10^–34 Дж×с; σ = 5,7×10^–8 Вт/м²К⁴.

7. Чему равна длина волны де Бройля электрона в водородноподобном атоме при вращении по стационарной орбите с радиусом 10^–9 м, если его орбитальный момент импульса при этом равен 10^–33 кг×м²/с? Принять 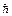= 10^–34 Дж×с.

8. Микрочастица с массой m = 5×10^–30 кг движется в области с нулевой потенциальной энергией и имеет волновую функцию ψ = А(sinαx + cosαx), где A = const, α = 2×10¹⁰ м^–1. Считая, что 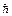= 10^–34 Дж×с, найти полную энергию микрочастицы (в эВ).

9. Если пренебречь спиновыми эффектами, то наибольшая величина силы, которая действует на один из возбужденных атомов водорода, находящихся в неоднородном внешнем магнитном поле с градиентом индукции |grad B| = 210 Тл/м, равна F_max = 7,812×10^–21 Н. Найти максимальный орбитальный момент импульса электрона в таких атомах. Магнетон Бора равен m_Б = 9,3×10^–24 А×м²; 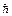= 10^–34 Дж×с.

10. В кубическом кристалле первого проводника имеется N₁ = 6,4×10²⁴ свободных электронов, а их средняя энергия при Т = 0 К равна 3,2 эВ. В другом таком же по форме и объему образце содержится N₂ = 2,7×10²⁴ свободных электронов. Найти энергию Ферми Е_ф2 для второго проводника в электронвольтах (при Т = 0 К).

11. Собственный полупроводник охлаждают от температуры 300 К до температуры 250 К. При этом его проводимость убывает в ехр(2) раз. Найти ширину запрещенной зоны этого полупроводника в электронвольтах. Постоянная Больцмана k = 1,38×10^–23 Дж/К.

12. Изотоп калия со средним временем жизни 100 лет образуется в растущей древесине. В исследуемом куске дерева концентрация атомов такого изотопа оказалась меньше в 10 раз. Сколько времени прошло с момента, когда было срублено дерево? Учесть, что ln 10 = 2,3.

Вариант №3

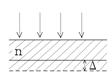
1. 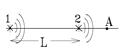Два точечных источника радиоволн с λ = 48 м расположены на расстоянии L = 2 км друг от друга и излучают со сдвигом фаз φ. Электрическое поле источника 1 изменяется со временем t по закону Е₁ = Е_ocosωt, а источника 2 Е₂= Е_ocos(ωt + φ). При каком наименьшем по величине сдвиге фаз j (в градусах) результирующая волна будет иметь максимальную амплитуду в любой точке А на продолжении линии, соединяющей источники?

2. 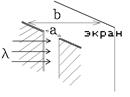Минимальная толщина плоской стеклянной пластинки, расположенной в вакууме и не отражающей падающие нормально лучи красного света (l_k = 680 нм) равна d = 170 нм. Слой какой минимальной толщины Δ надо сошлифовать с пластинки, чтобы она перестала отражать падающие нормально лучи синего света (l_c = 480 нм)?

3. 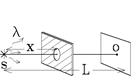В тонком плоском металлическом листе сделана узкая прорезь ширины a = 0,1 мм, на которую падает нормально плоская световая волна с λ = 500 нм. За металлическим листом на расстоянии b = 2 м стоит параллельный экран. Ширина дифракционного изображения - это расстояние между первыми дифракционными минимумами. Найти ширину дифракционного изображения прорези на экране.

4. Расстояние от точечного источника света S до вертикально расположенного экрана равно SO = L = 2 м. Линия SO совпадает с осью круглого отверстия радиуса r = 0,3 мм в плоской непрозрачной вертикальной перегородке. На каком расстоянии x от источника света S надо установить эту перегородку, чтобы освещенность в точке О экрана стала максимальной? λ = 500 нм.

5. Фотон с длиной волны λ = 1,105×10^–6 м вырывает из металла нерелятивистский электрон. Чему равна работа выхода А (в электронвольтах) для этого металла, если электрон вылетает с импульсом р = 2,4×10^–25 кг×м/с? h = 6,63×10^–34 Дж×с, с = 3×10⁸ м/с, масса электрона m = 9×10^–31 кг.

6. По проводу длины L = 30 см и диаметра d = 1 мм с удельным сопротивлением ρ = 9,12×10^–5 Ом×м течет постоянный ток I= 5 А. Считая провод абсолютно черным телом, найти его температуру. Принять σ = 5,7×10^–8 Вт/м²К⁴, π² = 10.

7. При увеличении энергии нерелятивистского электрона на ΔЕ= 300 эВ его дебройлевская длина волны изменилась в два раза. Найти первоначальную кинетическую энергию электрона (в эВ).

8. Состояние электрона с массой m = 9×10^–31 кг описывается волновой функцией ψ(r) = exp(ikr)/r, где r - модуль радиус-вектора, - мнимая единица, k = 1,2×10¹⁰ м^–1. Найти кинетическую энергию этого электрона (в эВ). Принять 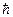= 10^–34 Дж×с; в случае радиальной координаты .

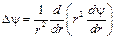9. Пучок возбужденных атомов водорода, в которых электроны находятся в состоянии 3d, влетает в неоднородное магнитное поле с градиентом индукции |grad B| = 3 Тл/м. Учитывая спиновые моменты электронов и пренебрегая спиновыми моментами ядер, определить максимальную возможную величину силы, действующей на атом водорода. Магнетон Бора равен m_Б = 9,3×10^–24 А×м².

10. Два одинаковых металлических кубика из разнородных металлов находятся при температуре Т = 0 К. Металл, из которого сделан первый кубик, имеет уровень Ферми Е_ф1 = 5 эВ, а свободных электронов в первом кубике в 125/64 раз больше, чем во втором кубике. Найти уровень Ферми Е_ф2 для металла, из которого изготовлен второй кубик (в эВ).

11. На сколько градусов ΔT надо нагреть полупроводник с шириной запрещенной зоны 0,207 эВ и с начальной температурой Т_o = 300 К, чтобы его собственная проводимость возросла в е = 2,72 раза? Постоянная Больцмана k = 1,38×10^–23 Дж/К.

12. Определить возраст древних деревянных предметов, в которых ежесекундно происходит в 2^1/5 меньше распадов ядер изотопа С¹⁴, чем в таком же количестве только что срубленной древесины. Период полураспада С¹⁴ равен 6000 лет и его концентрация постоянна в растущей древесине.

Вариант №4

1. 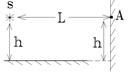Точечный источник S, испускающий электромагнитные волны с λ = 6 м, находится на расстоянии L = 4,5 м от вертикального экрана. В точке А этого экрана, расположенной на такой же высоте h над горизонтальным плоским зеркалом, что и источник S, наблюдается интерференционный максимум. При какой наименьшей высоте h это возможно?

2. На горизонтально расположенную в воздухе плоскую стеклянную пластинку с показателем преломления n = 1,5 падает вертикально белый свет. Если этот свет предварительно пропустить через светофильтр, то пластинка не будет отражать свет, пропущенный как через красный (l_k = 600 нм), так и через синий (l_c = 450 нм) светофильтр. Какова наименьшая возможная толщина пластинки?

3. Плоская монохроматическая световая волна с λ = 600 нм падает нормально на узкую щель ширины a = 6 мм. За щелью на большом удалении стоит параллельный ей экран. Чему равно расстояние b от щели до экрана, если расстояние между первым и вторым дифракционными минимумами на экране (по одну сторону от главного максимума освещенности) равно Δx = 12 мм?

4. 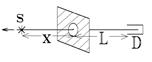Детектор D расположен на оси круглого отверстия в бесконечном плоском металлическом листе. Точечный источник радиоволн с λ = 4 см первоначально находился в центре О отверстия, а затем его перемещают вдоль оси. На какое наибольшее расстояние х надо удалить источник S от центра отверстия О, чтобы детектор перестал регистрировать радиоволны? Расстояние от листа до детектора L = 12 м, радиус отверстия r = 40 см.

5. Фотоэффект для некоторого металла начинается при частоте света n_o = 5,2×10¹⁵ Гц. Найти частоту света, вырывающего из металла электроны, которые полностью задерживаются разностью потенциалов U_з = 19,89 В. Заряд электрона е = 1,6×10^–19 Кл; постоянная Планка h = 6,63×10^–34 Дж×с.

6. Температура раскаленной нити в 75-ваттной лампочке Т = 5000 К. Ее энергетическая светимость составляет 40% от энергетической светимости абсолютно черного тела при той же температуре. Чему равна площадь поверхности нити S? Принять постоянную Стефана-Больцмана равной σ = 6×10^–8 Вт/м²К⁴.

7. Длина волны де Бройля электрона в водородоподобном атоме, находящемся в основном состоянии, равна 7,85×10^–9 м. Чему равен радиус второй боровской орбиты в этом атоме?

8. Микрочастица с массой m = 3×10^–30 кг находится в постоянном потенциальном поле U = 1 эВ и имеет волновую функцию ψ = A×exp(αx+βy+γz), где A = const,α = β =4×10⁹ м^–1, γ = 2×10⁹ м^–1. Полагая 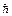= 10^–34 Дж×с, найти полную энергию Е микрочастицы (в электрон-вольтах).

9. Пучок электронов влетает в неоднородное магнитное поле. Спиновые эффекты приводят к появлению дополнительной к силе Лоренца силы F_c, действующей на электрон. Модуль этой силы равен F_c = 2,511×10^–21 Н, магнетон Бора m_Б = 9,3×10^–24 А×м². Определить величину градиента магнитного поля |grad B|.

10. Средняя энергия свободных электронов в металле при T_o = 0 К равна <Е> = 2,76 эВ. Найти отношение числа носителей тока в нем к числу электронов из зоны проводимости при температуре Т = 320 К. Постоянная Больцмана k = 1,38×10^–23 Дж/К.

11. Произведение концентраций свободных носителей заряда в собственном полупроводнике при температурах Т₁= 270 К и Т₂ = 330 К равно квадрату концентрации свободных носителей при температуре Т₃, т.е. n₁×n₂ = n₃². Найти температуру Т₃.

12. Исследуемый образец состоит из атомов двух различных радиоактивных изотопов с периодом полураспада Т₁ = 4 минуты и Т₂ = 3 минуты. В начальный момент времени образец содержал N_o1 = 3×10²⁰ атомов первого изотопа. Сколько всего атомов было в образце в начальный момент времени, если за последующие 12 минут распалось столько же атомов первого изотопа, сколько и второго?

Вариант №5

1. 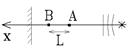Генератор испускает монохроматическую электрогмагнитную плоскую волну в направлении оси Ох. Перпендикулярно этой оси расположено металлическое зеркало, отражающее волну. В точках А и В на оси Ох, разделенных расстоянием L = 6 мм, наблюдаются два последовательных интерференционных минимума. Чему равна частота ν генератора? Скорость света с = 3∙10⁸ м/с.

2. Горизонтально расположенная в воздухе мыльная пленка с показателем преломления n = 1,35 образует клин с очень острым углом α = 5∙10^–6 рад. На каком расстоянии b друг от друга видны в отраженном вертикально свете соседние красные (l_k = 693 нм) интерференционные полосы на поверхности пленки?

3. Лучи эеленого (l_з = 560 нм) и красного (l_k= 700 нм) света падают нормально на дифракционную решетку. Какое наименьшее значение может иметь период d решетки, чтобы главные максимумы зеленого и красного цветов были видны за решеткой под одним и тем же углом φ = 30°?

4. Лазер мощностью 1мВт генерирует монохроматическое излучение с длиной волны равной0,6 мкм. За какое время лазер испускает фотоны, суммарная масса которых равна массе покоя электрона?

5. Поток одинаковых фотонов падает на два разных металла и вызывает фотоэффект. Скорость электронов, вылетающих из первого металла равна v₁ = 8×10⁵ м/с. При малейшем уменьшении частоты падающих фотонов фотоэффект на втором металле прекращается. Найти работу выхода электронов А₁ из первого металла (в эВ), если работа выхода для второго металла равна А₂ = 4,34 эВ, а масса электрона m = 9,1×10^–31 кг.

6. Поверхность абсолютно черного тела нагрета до температуры Т. Затем одну половину этой поверхности нагрели до вдвое большей температуры, а другую половину охладили до вдвое меньшей температуры. Во сколько раз увеличится поток энергии, излучаемый таким телом?

7. Фотоны с длиной волны λ = 2,2×10^–7 м падают на металл с работой выхода А = 7×10^–19 Дж. Найти минимальную длину дейбролевской волны электрона, выбитого из металла. Принять массу электрона равной m = 9×10^–31 кг; h = 6,6×10^–34 Дж×с.

8. Стационарное состояние частицы с массой m= 10^–30 кг определяется волновой функцией ψ = Aexp(iαr)/r, которая зависит только от модуля радиус-вектора r; А = const, - мнимая единица.. В этом состоянии кинетическая энергия частицы равна 8×10^–18 Дж. Найти величину постоянной α (в м^–1), принимая 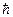= 10^–34 Дж×с и используя в случае радиальной координаты правило .

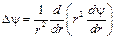9. 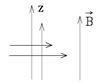В опыте Штерна - Герлаха в неоднородное магнитное поле, индукция которого возрастает вдоль вертикальной оси Оz по закону В =αz, где α = 2 Тл/м, влетает горизонтальный пучок возбужденных атомов водорода, электроны в которых находятся в 5f состоянии. Пренебрегая спиновыми моментами электронов и ядер, определить максимальную величину силы, действующей на атом водорода. Магнетон Бора m_Б = 9,3×10^–24 А×м².

10. Во сколько раз возрастает число носителей тока в проводнике, если первоначально он имел комнатную температуру t_o = 23°С и был затем нагрет на Δt° = 60°C?

11. При нагревании собственного полупроводника с начальной температурой Т = 200 К на ΔT = 50 К его проводимость возрастает в ехр(2) раз. Во сколько раз возрастет проводимость этого полупроводника при его нагревании от начальной температуры Т до температуры Т + 4DT?

12. В начальный момент времени концентрация атомов первого радиоактивного изотопа в некотором образце в 16 раз меньше, чем концентрация атомов второго изотопа. Периоды полураспада этих изотопов равны, соответственно, Т₁ = 5 с и Т₂ = 3 с. Через какой промежуток времени t концентрации двух изотопов в образце сравняются?

Вариант №6

1. 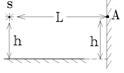Точечный источник S, испускающий электромагнитные волны с λ= 80 см и точка А на вертикальном экране находятся на одинаковой высоте h = 1 м над горизонтальным плоским зеркалом. При каком максимальном расстоянии L между источником S и экраном в точке А можно наблюдать интерференционный максимум?

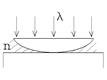
2. Найти радиус первого светлого (голубого) кольца Ньютона в установке, в которой интерференция наблюдается в отраженном свете. Стеклянная линза радиусом R = 7,8 м лежит на стеклянной пластинке и пространство между ними заполнено жидкостью с показателем преломления n = 1,3 < n_стекла. На линзу нормально падает свет сλ = 480 нм.

3. Сколько главных максимумов будет видно за дифракционной решеткой, изготовленной нанесением N = 3000 равноудаленных штрихов на прозрачную полоску длины L = 1 см? Свет с длиной волны λ = 600 нм падает на решетку нормально.

4. Какой импульс передает фотон светового излучения с длиной волны 6,6∙10^-7 м идеальному зеркалу, полностью отражающему свет?

5. Фотон с импульсом р = 2,4×10^–26 кг×м/с поглощается атомом и выбивает из него электрон с кинетической энергией К = 21 эВ. Найти энергию ионизации этого атома (в эВ). с = 3×10⁸ м/с.

6. Начальная температура абсолютно черного тела Т = 2500 К. На сколько градусов уменьшилась эта температура, если наиболее вероятная длина волны в спектре излучения такого тела, первоначально равная l_m = 1160 нм, увеличилась на Δλ = 90 нм?

7. Фотон с импульсом р = 1,4×10^–28 кг×м/с выбивает из металла электрон с дебройлевской длиной волны l_б = 1,1×10^–8 м. Найти работу выхода электрона из этого металла (в эВ). Принять массу электрона равной m= 9×10^–31 кг; h = 6,6×10^–34 Дж×с; с = 3×10⁸ м/с.

8. Частица с массой m = 10^–30 кг находится в двумерном потенциальном поле U(x,y) = 2b² 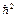(x²+y²)/m и имеет волновую функцию ψ = A×exp[b(x²+y²)], где А = const, b = 1,2×10²⁰ м^–2. Полагая 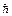= 10^–34 Дж×с, найти полную энергию Е частицы в таком состоянии (в электрон-вольтах).

9. В атомах бора В₅ электрон, находящийся в основном состоянии в подоболочке 2p, переходит на более высокий энергетический уровень, причем величина его орбитального магнитного момента возрастает в 6 раз. На сколько отдельных пучков разделится пучок возбужденных подобным образом атомов бора в неоднородном магнитном поле? Спиновыми эффектами пренебречь.

10. Чему равна энергия Ферми (в эВ) в проводнике, в котором при комнатной температуре 300 К средняя энергия электрона из зоны проводимости в 64 раза больше его возможной тепловой энергии? Постоянная Больцмана k = 1,38×10^–23 Дж/К.

11. В собственном полупроводнике уровень Ферми расположен на расстоянии 0,5 эВ от нижнего уровня зоны проводимости. Во сколько раз надо повысить первоначальную температуру этого полупроводника T_o, чтобы его проводимость возросла в е = 2,72 раз? Известно, что k×Т_o = 0,3 эВ, где k - постоянная Больцмана.

12. Концентрации атомов двух различных радиоактивных изотопов одинаковы в начальный момент времени t_o = 0. За последующий интервал времени Δt = 1 сек распадается в 1,75 раз больше ядер первого изотопа, чем второго. Чему равна постоянная распада l₁ первого изотопа, если постоянная распада второго изотопа равна l₂ = ln 2 = 0,69 с^–1?

Вариант №7

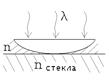
1. 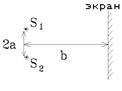В интерференционной схеме расстояние между расположенными на вертикальной линии когерентными источниками S₁ и S₂ равно 2a = 2000 нм. На каком расстоянии b от вертикального экрана должны находиться эти источники, чтобы ширина интерференционных полос на экране была равна a= 1000 нм? Источники испускают свет с длиной волны λ = 800 нм с одной начальной фазой.

2. 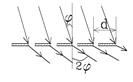Стеклянная линза радиусом R = 280 см лежит на стеклянной плоской пластинке. Пространство между ними заполнено жидкостью c показателем преломления n = 1,4 < n_стекла. Найти длину волны λ падающего нормально света, если радиус первого светлого кольца Ньютона в отраженном свете равен r₁ = 0,7 мм.

3. Лучи света с λ = 720 нм падают на дифракционную решетку под углом φ = arccos(0,8) к нормали. Постоянная решетки d не должна превышать 5λ. Какой должна быть эта постоянная d, чтобы за решеткой главный максимум наблюдался под углом 2φ?

4. Сетчатка глаза начинает реагировать на желтый свет с длиной волны 600 нм при мощности падающего на нее излучения 1,98∙10^-18 Вт. Сколько фотонов при этом падает на сетчатку каждую секунду?

5. На металл с работой выхода 2,6 эВ падал пучок фотонов с энергией 3,9 эВ и выбивал электроны, вылетающие с некоторой скоростью. Длину волны фотонов уменьшили в 6 раз. Во сколько раз увеличилась скорость выбиваемых электронов?

6. В излучении абсолютно черного тела с температурой Т₁= 800 К наибольшее число фотонов имеет импульс р₁ = 1,2×10^–25 кг×м/с. До какой температуры Т₂ надо нагреть это тело, чтобы максимум излучения приходился на фотоны с импульсом р₂ = 1,5×10^–25 кг×м/с?

7. Испытывая рассеяние на покоящейся частице, имеющей комптоновскую длину волны l_k = 4,5×10^–12 м, фотон улетает под прямым углом к направлению первоначального движения, а его энергия при этом уменьшается в 4 раза. Найти частоту ν налетающего фотона до рассеяния. с = 3×10⁸ м/с.

8. Частица движется в одномерном потенциальном поле U(x) = b 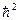/mx, где 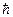= 10^–34 Дж×с, b = 4×10¹⁰ м^–1. Волновая функция частицы равна ψ = Aх×ехр(bх), где A = const. Найти массу частицы m, если ее полная энергия в этом состоянии равна Е = – 5 эВ.

9. Разность частот в спектре атома, возникающая из-за спин-орбитального взаимодействия, равна Dn = 8,4×10¹⁰ Гц. Найти эффективное значение индукции магнитного поля, действующего на спиновый момент электрона в атоме, и созданного движением других электронов в нем. Магнетон Бора равен m_Б = 9,24×10^–24 А×м²; h = 6,6×10^–34 Дж×с.

10. В проводнике с энергией Ферми 6,9 эВ средняя энергия электрона из зоны проводимости в 100 раз больше тепловой энергии, которую может приобрести этот электрон. Определить температуру проводника (в К). Постоянная Больцмана k = 1,38×10^–23 Дж/К.

11. Собственный полупроводник с начальной температурой T_o = 320 К охлаждается на ΔT = 120 К. При этом концентрация дырок в нем уменьшается в ехр(5) раз. Найти ширину запрещенной зоны этого полупроводника (в эВ). Постоянная Больцмана k = 1,38×10^–23 Дж/К.

12. В начальный момент времени t_o = 0 концентрации атомов двух различных радиоактивных изотопов в образце одинаковы. За последующую секунду в образце сохранилось в два раза больше ядер первого изотопа, чем ядер второго изотопа. Найти период полураспада Т₂ второго изотопа, если период полураспада первого изотопа равен Т₁ = 3 с.

Вариант №8

1. 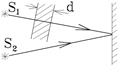В интерференционном опыте Юнга когерентные источники S₁ и S₂ испускают в вакууме свет с l = 720 нм в одной фазе. После того, как на пути луча, идущего от одного из источников поставили тонкую стеклянную пластинку толщиной d = 4∙10^–7 м, на месте центрального (нулевого) максимума на удаленном экране оказался соседний интерференционный минимум. Чему равен показатель преломления n стекла?

2. Найти радиус R стеклянной линзы, лежащей на плоской стеклянной пластинке, если в отраженном свете с λ = 600 нм два соседних темных кольца Ньютона имеют радиусы 0,5 мм и 0,4 мм. Пространство между линзой и пластинкой заполнено жидкостью с показателем преломления n = 2, где n > n_стекла.

3. Лучи света с λ = 600 нм падают на дифракционную решетку под углом φ = 30° к нормали. За решеткой последний максимум виден под углом α. Найти sinα, если постоянная решетки равна d = 21 мкм.

4. Мощность излучения Солнца равна 3,75∙10²⁶ Дж/с. Чему равно ежесекундное уменьшение массы Солнца?

5. Ренгтеновское излучение с частотой n₁= 1,8×10¹⁸ Гц вырывает из некоторого металла электроны с кинетической энергией в пять раз большей, чем кинетическая энергия электронов, вырываемых из того же металла излучением с частотой ν₂ = ν₁/3. При какой частоте ν₃ излучения оно прекратит вырывать электроны из этого металла.

6. Диаметр спирали в электрической лампочке равен 0,1 мм, длина спирали – 10 см. При включении лампочки в цепь напряжением 100 В через лампочку течет ток силой 0,1 А. Принимая, что излучение нити соответствует излучению абсолютно черного тела, определить ее энергетическую светимость.

7. Фотон с импульсом р₁ = 5×10^–26 кг×м/с сталкивается с покоящейся частицей и, испытывая комптоновское рассеяние, улетает с импульсом р₂ = 2×10^–26 кг×м/с в направлении, противоположном первоначальному направлению движения фотона. Найти комптоновскую длину волны данной частицы. Принять h = 6,6×10^–34 Дж×с.

8. Микрочастица с массой m = 3×10^–30 кг имеет волновую функцию 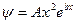и движется в одномерном потенциальном поле 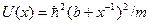, где А = const, b = 1,2×10¹⁰ м^–1. Полагая 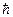= 10^–34 Дж×с, определить полную энергию микрочастицы (в эВ).

9. Атомарный водород, находившийся в основном состоянии (энергия атома в основном состоянии равна - 13,5 эВ) нагревают до постоянной температуры Т = 600 К и помещают во внешнее магнитное поле с индукцией В = 5 Тл. Способен ли такой нагретый водород излучать, и если да, то фотоны с какой частотой ν он излучает? Магнетон Бора принять равным m_Б = 9,24×10^–24 А×м²; h= 6,6×10^–34 Дж×с; k = 1,38×10^–23 Дж/К.

10. Средний квадрат модуля скорости электронов с массами m = 9×10^–31 кг из зоны проводимости проводника равен 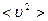= 6,4×10¹¹ м²/с². Найти энергию Ферми для этого проводника (в эВ), если его температура Т = 0 К.

11. При нагревании собственного полупроводника натуральный логарифм концентрации свободных носителей заряда увеличился на 16. До какой температуры нагрели полупроводник, если его начальная температура была равна 200 К, а уровень Ферми лежит на расстоянии 0,46 эВ от верхнего уровня валентной зоны? k = 1,38×10^–23 Дж/К.

12. Изготовлен образец некоторого радиоактивного элемента. Через промежуток времени Δt = 2 дня после начала распада сохранятся 10 % атомов этого элемента. Сколько еще дней следует подождать, чтобы сохранилось 0,01 % от первоначального числа радиоактивных атомов в таком образце?

Вариант №9

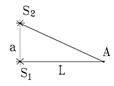
1. Два когерентных источника света S₁ и S₂ с длиной волны λ = 400 нм и точка наблюдения А расположены в вершинах прямоугольного треугольника. Расстояние между источниками S₁S₂ = a = 4 мм. На каком максимальном расстоянии L от точки А должен находиться ближайший к этой точке источник S₂, чтобы в точке А наблюдался интерференционный максимум? Учесть, что λ << a.

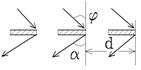
2. 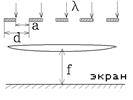Найти минимальную толщину пленки с показателем преломления n = 1,33, при которой свет с длиной волны λ₁ = 0,64 мкм испытывает максимальное отражение, а свет с длиной волны λ₂ = 0,4 мкм не отражается совсем. Угол падения света α = 30˚.

3. Монохроматический свет с длиной волны λ падает нормально на дифракционную решетку с периодом d = 8λ и с шириной каждой щели a = 2λ. За решеткой стоит линза, собирающая все лучи, выходящие из решетки, на экране, расположенном в фокальной плоскости линзы. Сколько полос (интерференционных максимумов) будет видно на экране?

4. 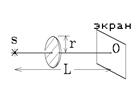Расстояние от точечного источника монохроматического света S до экрана равно L = 4 м. Если посредине между источником и экраном поставить плоское непрозрачное препятствие с вырезанным в нем круглым отверстием, то в центральной точке экрана наблюдается самая большая освещенность. На какое расстояние надо сдвинуть препятствие с вырезом в сторону источника света, чтобы освещенность в центральной точка стала самой малой.

5. Фотокатод, покрытый кальцием (работа выхода А = 4,42∙10^-19 Дж), освещается светом частотой ν = 2∙10¹⁵ Гц. Вылетевшие из катода электроны попадают в однородное магнитное поле перпендикулярно линиям индукции этого поля и движутся по окружности радиусом R = 5 мм. Чему равна индукция магнитного поля В?

6. Диаметр спирали в электрической лампочке равен 0,1 мм, длина спирали – 10 см. При включении лампочки в цепь напряжением 100 В через лампочку течет ток силой 0,1 А. Найти температуру лампочки. Считать, что по установлении равновесия все выделяющееся тепло теряется в результате лучеиспускания. Принять отношение энергетических светимостей спирали и абсолютно черного тела равным 0,31.

7. Фотон налетает на покоящуюся частицу и, испытывая комптоновское рассеяние, отклоняется на угол 60° от первоначального направления движения. Его энергия уменьшается при этом в три раза. Найти величину импульса фотона до рассеяния, если комптоновская длина волны частицы равна l_k = 6×10^–12 м; h = 6,6×10^–34 Дж×с.

8. Состояние частицы с массой m = 5×10^–30 кг описывается волновой функцией ψ = Ax^1/2exp(bx), где А = const, b = 4×10¹⁰ м^–1. При этом частица движется в одномерном потенциальном поле 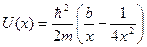. Полагая 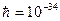Дж×с, найти полную энергию частицы в таком состоянии (в электрон-вольтах).

9. Найти длину волны фотона, испускаемого при переходе электрона между соседними уровнями, возникающими в результате зеемановского расщепления, когда атом водорода находится в магнитном поле с индукцией 5 Тл. Принять магнетон Бора равным m_Б =9,9×10^–24 А×м²; h = 6,6×10^–34 Дж×с; c = 3×10⁸ м/с.

10. Средние энергии электронов из зоны проводимости в двух разных металлах при температуре T_o= 0 К равны соответственно <E>₁= 3 эВ и <E>₂ = 4 эВ. Отношение концентрации носителей тока к концентрации свободных электронов из зоны проводимости в этих металлах одинаково. Чему равна температура Т₂ второго металла, если температура первого Т₁ = 300 К?

11. При повышении температуры концентрация основных носителей заряда в полупроводнике n-типа не превышает 10²⁶ м^–3. Кристалл полупроводника имеет объем 1 см³ и состоит из 8×10²² атомов. Какова концентрация атомов примеси (в %) в этом полупроводнике?

12. В начальный момент времени t_о = 0 образец радиоактивного материала содержит 10¹² радиоактивных атомов с периодом полураспада Т = 25 часов. Сколько атомов этого материала распадается за промежуток времени от t₁ = 100 с до t₂ = 200 с? Принять ln 2 = 0,693; ехр(х) ~ 1+х при х << 1.

Вариант №10

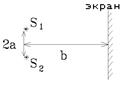
1. В интерференционной схеме расстояние между расположенными на вертикальной линии когерентными источниками S₁ и S₂ равно 2a = 2000 нм. Расстояние от вертикального экрана до источников равно b = 5 см. Источники испускают свет с длиной волны λ = 800 нм с одной начальной фазой. Найти ширину интерференционной полосы.

2. На поверхности стекла находится пленка воды. На нее падает свет с длиной волны λ = 0,68 мкм под углом α = 30˚ к нормали. Найти скорость, с которой уменьшается толщина пленки в результате испарения, если интенсивность отраженного света меняется так, что промежуток времени между последовательными максимумами отражения Δt = 15 минут.

3. Угловая дисперсия дифракционной решетки для длины волны λ = 668 нм в спектре первого порядка равна 2,02∙10⁵ рад/м. Найти период решетки.

4. Точечный источник монохроматического электромагнитного излучения находится на оси отверстия с радиусом r = 6 мм, вырезанного в бесконечном металлическом листе. Детектор D, находящийся на этой же оси за отверстием, фиксирует два последовательных минимума интенсивности излучения на расстояниях L₁ = 40 м и L₂ = 36 м от металлического листа. Найти длину волны излучения.

5. В вакууме находятся два покрытых кальцием электрода, к которым подключен конденсатор емкостью С. При длительном освещении катода светом длиной волны λ = 300 нм фототок, возникший вначале, прекращается, а на конденсаторе появляется заряд q = 11∙10^-9 Кл. Работа выхода электронов из кальция А = 4,42∙10^-19 Дж. Определить емкость конденсатора.

6. Какой поток энергии получает комната через открытую дверцу в которой поддерживается температура Т = 1000 К? Размер дверцы 10×15 см. Считать, что отверстие печи излучает как черное тело.

7. Найти длину волны света, вырывающего с поверхности металла электроны, полностью задерживающиеся обратным потенциалом U = 1 В. Фотоэффект у этого металла начинается при частоте падающего света ν_о = 10¹⁵ с^-1.

8. Частица с массой m = 5×10^–30 кг находится в одномерном потенциальном поле U(x) = 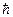²(2ах + b)²/2m и имеет волновую функцию ψ = Аехр(ах² + bх + с), где А, а, b, с - постоянные величины. Найти величину а (в м^–2), если полная энергия частицы равна Е = – 4 эВ; 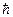= 10^–34 Дж×с.

9. Чему равна частота радиоизлучения водорода, находящегося в сильном магнитном поле с индукцией 6 Тл (переходы между соседними, расщепленными в результате действия магнитного поля уровнями)? Магнетон Бора m_Б = 9,24×10^–24 А×м²; h = 6,6×10^–34 Дж×с. Спиновыми эффектами пренебречь.

10. При охлаждении металла число носителей тока в нем изменилось в 2 раза. До какой температуры охладили металл, если его первоначальная температура 17°C?

11. Донорные уровни энергии полупроводника n- типа расположены на расстоянии 0,01 эВ от нижней границы зоны проводимости. Оценить отношение концентраций примесных носителей тока n₁/n₂ в таком полупроводнике при температурах Т₁ = 400 К и Т₂ = 500 К. Постоянная Больцмана k = 1,38×10^–23 Дж/К.

12. В начальный момент t_o = 0 концентрации атомов двух различных радиоактивных изотопов в образце одинаковы. В момент времени t₁ = t атомов первого изотопа будет в 5 раз больше, чем атомов второго. Найти отношение концентраций сохранившихся атомов первого изотопа к концентрации атомов второго изотопа в момент времени t₂= 4t.

Date: 2015-08-06; view: 2062; Нарушение авторских прав