Список задач к практическим занятиям

1. Элементарная оптика

· На краю бассейна стоит человек и наблюдает камень, лежащий на дне. Глубина бассейна h. На каком расстоянии от поверхности воды видно изображение камня, если луч зрения составляет с нормалью к поверхности воды угол j₀.

· Показать, что при преломлении в призме с малым преломляющим углом q луч отклоняется на угол 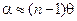независимо от угла падения, если последний также мал.

· Луч света проходит через призму с преломляющим углом q и показателем преломления n. Пусть a – угол отклонения луча. Показать, что при симметричном ходе луча через призму:

а) угол a минимален;

б) связь между углами a и q определяется формулой:

.

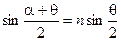· Найти пределы, в которых может меняться угол отклонения луча при прохождении стеклянной призмы с преломляющим углом q=60°.

· Трехгранная призма с преломляющим углом 60° дает угол наименьшего отклонения в воздухе 37°. Какой угол наименьшего отклонения даст эта призма в воде?

· Луч света, содержащий две монохроматические составляющие, проходит через трехгранную призму с преломляющим углом q=60°. Определить угол Da между обеими составляющими луча после призмы, если показатели преломления для них равны 1,515 и 1,520 и призма ориентирована на угол наименьшего отклонения.

2. Электромагнитные волны. Давление света

· Электрический пробой в воздухе наступает примерно при напряженности электрического поля 3 МВ/м. При какой плотности потока энергии плоских электромагнитных волн можно наблюдать искру в воздухе?

· Точечный источник мощностью 1 Вт излучает равномерно по всем направлениям фотоны с длиной волны 0,5 мкм. Какова плотность потока фотонов на расстоянии 1 км от источника?

· Найти амплитуды напряженностей электрического и магнитного полей волны, плотность потока энергии которой 1 Вт/м².

· Найти амплитуду напряженности магнитного поля волны, распространяющейся в воде (n=1,33), и плотность потока энергии волны, если амплитуда электрического поля 20 кВ/м.

· Найти среднюю напряженность электрического поля излучения Солнца на Земле, принимая для солнечной постоянной значение 2 кал/(см²×мин) и пренебрегая поглощением в атмосфере. Солнечной постоянной называется средний поток солнечной радиации, приходящейся на 1 см² земной поверхности, перпендикулярной к направлению излучения, в 1 мин (при отсутствии поглощения в атмосфере).

· Исходя из представления, что свет состоит из фотонов, каждый из которых обладает импульсом hn/с, определить давление P световой волны на плоское зеркало, предполагая, что коэффициент отражения зеркала равен r, а угол падения равен j. Определить также тангенциальную силу T, действующую на единицу поверхности зеркала со стороны падающего излучения.

· Решить предыдущую задачу в предположении, что поверхность, на которую падает световая волна, идеально матовая (удовлетворяет закону Ламберта).

· Чему равно световое давление при нормальном падении света на полностью отражающую поверхность при плотности потока энергии волн 1 Вт/м²?

· Найти световое давление солнечного излучения на квадратный метр земной поверхности, перпендикулярной к направлению излучения. Солнечная постоянная равна 2 кал/(см²×мин). Абсорбцией в земной атмосфере пренебречь. Рассмотреть три случая:

o земная поверхность – абсолютно черная;

o земная поверхность – абсолютно зеркальная;

o земная поверхность – абсолютно отражающая, но матовая (удовлетворяет закону Ламберта).

· Лазер на рубине излучает в импульсе длительностью t=0,5 мс энергию W=1 Дж в виде почти параллельного пучка с сечением s=1 см². Рабочая длина волны лазера l=0,6943 мкм. Определить следующие величины: 1) давление несфокусированного пучка света Р на площадку, перпендикулярную к пучку; 2) давление света Р на площадку, перпендикулярную к пучку, при максимально возможной концентрации светового пучка (при фокусировке в область с площадью поперечного сечения порядка l²); 3) напряженность электрического поля Е в области максимально возможной концентрации светового пучка. Считать излучение лазера во время импульса равномерным (усреднение).

3. Поляризация света

· Линейно поляризованный световой пучок падает на поляризатор, вращающийся вокруг оси пучка с угловой скоростью w = 21 рад/с. Найти световую энергию, проходящую через поляризатор за один оборот, если поток энергии в падающем пучке F0 = 4 мВт.

· При падении естественного света на некоторый неидеальный поляризатор проходит 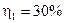светового потока, а через два таких поляризатора – 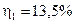. Найти угол j между плоскостями пропускания этих поляризаторов.

· На пути частично поляризованного света поместили поляризатор. При повороте поляризатора на угол 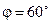из положения, соответствующего максимуму пропускания, интенсивность прошедшего света уменьшилась в раза. Найти степень поляризации падающего света.

· Две монохроматические волны, линейно поляризованные во взаимно перпендикулярных плоскостях, распространяются в одном направлении. В результате их наложения в общем случае получается свет, поляризованный по эллипсу. Как определить, зная разность фаз между складывающимися волнами, будет ли поляризации правой или левой?

· Какой характер поляризации имеет плоская электромагнитная волна, проекции вектора 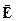которого на оси x и y, перпендикулярные к направлению ее распространения, определяются следующими уравнениями:

а) ;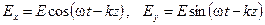

б) ;

в) .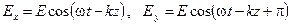

4. Дисперсия и поглощение света

· Электромагнитная волна с частотой w распространяется в разреженной плазме. Концентрация свободных электронов в плазме равна N. Пренебрегая взаимодействием волны с ионами плазмы, найти зависимость:

а) диэлектрической проницаемости плазмы от частоты;

б) фазовой скорости от длины волны l в плазме.

· Найти концентрацию свободных электронов ионосферы, если для радиоволн с частотой n = 100 МГц ее показатель преломления n = 0,90.

· Имея в виду, что для достаточно жестких рентгеновских лучей электроны вещества можно считать свободными, определить, насколько отличается от единицы показатель преломления графита для рентгеновских лучей с длиной волны в вакууме l = 50 пм.

· В ряде случаев диэлектрическая проницаемость вещества оказывается величиной комплексной или отрицательной и показатель преломления – соответственно комплексным (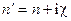) или чисто мнимым (). Написать для этих случаев уравнение плоской волны и выяснить физический смысл таких показателей преломления.

· При зондировании разреженной плазмы радиоволнами различных частот обнаружили, что радиоволны с 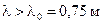испытывают полное внутреннее отражение. Найти концентрацию свободных электронов в этой плазме.

· В некоторой среде связь между групповой и фазовой скоростями электромагнитной волны имеет вид 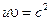, где с – скорость света в вакууме. Найти зависимость диэлектрической проницаемости этой среды от частоты волны e(w).

· Показатель преломления сероуглерода для света с длинами волн 509, 534 и 589 нм равен соответственно 1,647, 1,640 и 1,630. Вычислить фазовую и групповую скорости света вблизи l = 534 нм.

· Плоский световой импульс распространяется в среде, где фазовая скорость v линейно зависит от длины волны l по закону 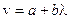, a и b – некоторые положительные постоянные. Показать, что в такой среде форма произвольного светового импульса будет восстанавливаться через промежуток времени .

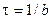· Вычислить групповую скорость u для различных законов дисперсии (v – фазовая скорость):

1) 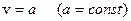– недиспергирующая среда, например, звуковые волны в воздухе;

2) 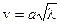– волны на поверхности воды, вызываемые силой тяжести;

3) 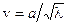– капиллярные волны;

4) 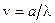– поперечные колебания стержня;

5) 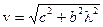– электромагнитные волны в ионосфере (с – скорость света в вакууме, l – длина волны в среде);

6) 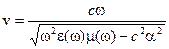– электромагнитные волны в прямолинейном волноводе, заполненном диспергирующей средой с диэлектрической проницаемостью 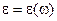и магнитной проницаемостью 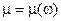(с – скорость света в вакууме, a – постоянная, зависящая от размеров и формы поперечного сечения волновода).

5. Отражение и преломление света на границе раздела сред

· Естественный свет падает под углом Брюстера на поверхность стекла. Определить с помощью формул Френеля:

а) коэффициент отражения;

б) степень поляризации преломленного света.

· Плоский пучок естественного света с интенсивностью I ₀ падает под углом Брюстера на поверхность воды. При этом 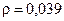светового потока отражается, Найти интенсивность преломленного пучка.

· Узкий пучок естественного света падает под углом Брюстера на поверхность толстой плоскопараллельной прозрачной пластины. При этом от верхней поверхности отражается 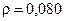светового потока. Найти степень поляризации пучков 1–4.

· Узкий пучок естественного света падает под углом Брюстера на стопу Столетова, состоящую из N толстых плоскопараллельных стеклянных пластин. Найти:

а) степень поляризации P прошедшего пучка;

б) чему равно P при N= 1, 2, 5, 10.

· Из стекла (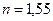) на границу раздела с воздухом под углом 60° падает световая волна. Найти критический угол и сдвиги фаз колебаний напряженности электрического поля 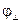и .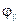

· При какой удельной электропроводимости затухание в среде (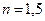) равно 1 дБ/км?

· Найти коэффициент пропускания при нормальном падении света из воздуха на стекло с показателем преломления .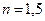

· Сколько процентов светового потока теряется на отражение в призматическом бинокле? Показатель преломления стекла призм и линз равен 1,5. Схема бинокля дана на рисунке.

· Проверить с помощью формул Френеля, что поток энергии падающей волны через границу раздела сред равен сумме потоков энергии преломленной и отраженной волн через ту же границу.

· Угол между плоскостью колебаний поляризованного света и плоскостью падения называется азимутом колебания. Найти азимут преломленной волны d и азимут отраженной волны r, если азимут падающей волны a, а угол падения j.

· При каком угле падения j разность фаз d между компонентой отраженной волны, поляризованной в плоскости падения, и компонентой, поляризованной перпендикулярно к ней, достигает максимума при полном внутреннем отражении, если падающая волна линейно поляризована? Чему равен этот максимум?

· Каким показателем преломления n должно обладать вещество, чтобы при помощи однократного полного внутреннего отражения на границе его с воздухом можно было превращать линейно поляризованный свет в поляризованный по кругу? Азимут колебаний падающего света равен 45°.

· Падающий свет поляризован линейно с азимутом колебаний, равным +45°. Можно ли путем однократного отражения превратить его в свет, поляризованный по правому кругу?

· Какой должен быть минимальный показатель преломления параллелепипеда Френеля, чтобы при азимуте колебаний падающего света в +45° выходящий свет был поляризован по правому кругу?

· Найти фазовый сдвиг между перпендикулярной и параллельной компонентами отраженной световой волны при полном внутреннем отражении.

6. Геометрическая оптика

· Линза представляет собой стеклянный шар радиуса R. Показатель преломления стекла n. Доказать, что главные плоскости этой линзы совпадают и проходят через центр шара. Найти фокусное расстояние линзы.

· Найти построением:

а) ход луча после отражения в вогнутом и выпуклом сферических зеркалах (см. рисунок), где F – фокус, OO’ – оптическая ось;

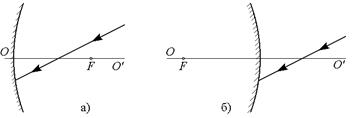
б) положение зеркала и его фокуса для случаев, показанных на рисунке, где P и P’ – сопряженные точки.

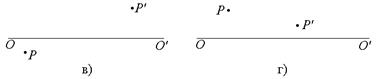
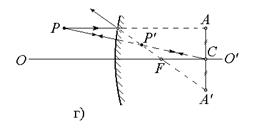
· Найти оптическую силу и фокусные расстояния:

а) тонкой стеклянной линзы в жидкости с показателем преломления , если ее оптическая сила в воздухе 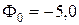дптр;

б) тонкой симметричной двояковыпуклой стеклянной линзы, с одной стороны которой находится воздух, а с другой – вода, если оптическая сила этой линзы в воздухе Ф₀ = +10 дптр.

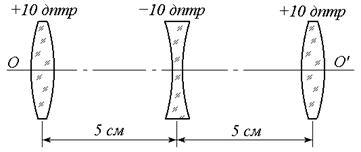
· На рисунке показана центрированная система, состоящая из трех тонких линз. Система находится в воздухе. Определить:

а) положение точки схождения параллельного пучка, падающего слева, после прохождения через систему;

б) расстояние от первой линзы до точки, находящейся на оси слева от системы, при котором эта точка и ее изображение будут расположены симметрично относительно системы.

· Найти фокусное расстояние f’ двояковыпуклой тонкой линзы, ограниченной сферическими поверхностями радиусами R ₁ = 25 мм и R ₂ = 40 мм; показатель преломления стекла линзы n = 1,5.

· Линза с фокусным расстоянием f = 10 см сделана из стекла с показателем преломления n = 1,5. Найти фокусное расстояние f’ линзы, помещенной в воду (n’ = 4/3).

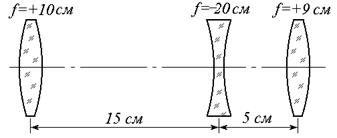
· На систему линз, изображенных на рисунке, падает слева параллельный пучок света. Найти положение точки схождения этого пучка после прохождения системы.

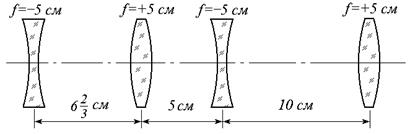
· Найти изображение точки, которая находится на расстоянии 10 см слева от крайней левой линзы системы, изображенной на рисунке.

· Фотографическим аппаратом, объектив которого имеет фокусное расстояние 12 см при растяжении 20 см, требуется сфотографировать предмет, находящийся на расстоянии 15 см от объектива. Какую линзу нужно добавить к объективу, чтобы изображение вышло резким при максимально возможном растяжении аппарата?

· Определить положения главных плоскостей, фокальных точек и фокусное расстояние системы двух тонких линз, изображенной на рисунке.

7. Интерференция света

· В интерферометре Майкельсона наблюдаются кольца равного наклона от ртутной лампы, испускающей свет с длиной волны l = 435,8 нм. При смещении подвижного зеркала интерферометра на 47,5 мм интерференционная картина размывается. Найти ширину линии.

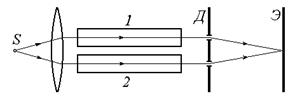
· На рисунке показана схема интерферометра для измерения показателей преломления прозрачных веществ. Здесь S – узкая щель, освещаемая монохроматическим светом с l = 589 нм, 1 и 2 – две одинаковые трубки с воздухом, длина каждой из которых l = 10 см, Д – диафрагма с двумя щелями. Когда воздух в трубке 1 заменили аммиаком, то интерференционная картина на экране Э сместилась вверх на N = 17 полос. Показатель преломления воздуха n = 1,000277. Определить показатель преломления аммиака.

· Для уменьшения потерь света из-за отражения от поверхности стекла последнюю покрывают тонким слоем вещества с показателем преломления , где n – показатель преломления стекла. В этом случае амплитуды световых колебаний, отраженных от обеих поверхностей такого слоя, будут одинаковыми. При какой толщине этого слоя отражательная способность стекла в направлении нормали будет равна нулю для света с длиной волны l?

· В двухлучевом интерферометре используется оранжевая линия ртути, состоящая из двух компонент с l₁=576,97 нм и l₂=579,03 нм. При каком наименьшем порядке интерференции четкость интерференционной картины будет наихудшей?

· В интерферометре Майкельсона использовалась желтая линия натрия, состоящая из двух компонент с длинами волн l₁=589,0 нм и l₂=589,6 нм. При поступательном перемещении одного из зеркал интерференционная картина периодически исчезала (почему?). Найти перемещение зеркала между двумя последовательными появлениями наиболее четкой картины.

· При освещении эталона Фабри-Перо расходящимся монохроматическим светом с длиной волны l в фокальной плоскости линзы возникает интерференционная картина – система концентрических колец. Толщина эталона равна d. Определить, как зависит от порядка интерференции: а) расположение колец; б) угловая ширина полос интерференции.

· Найти для эталона Фабри-Перо, толщина которого d = 2,5 см:

а) максимальный порядок интерференции света с длиной волны l=0,5 мкм;

б) дисперсионную область Dl, т.е. спектральный интервал длин волн, для которого еще нет перекрытия с другими порядками интерференции, если наблюдение ведется вблизи l=0,5 мкм.

· Найти длину волны l монохроматического излучения, если в опыте Юнга расстояние первого интерференционного максимума от центральной полосы x = 0,05 см, расстояние между щелями d = 0,5 см, расстояние от щелей до экрана наблюдения a = 5 м.

· Найти распределение интенсивности света на экране в установке с зеркалами Френеля при заданных: угле между зеркалами a, расстоянии от зеркал до экрана a, расстоянии от точечного источника света до ребра бизеркала r.

· Найти число полос интерференции N, получающихся с помощью бипризмы, если показатель преломления ее n, преломляющий угол a, длина волны источника l. Расстояние источника света от бипризмы равно a, а расстояние бипризмы от экрана равно b.

· Полосы интерференции получаются с помощью бипризмы Френеля с малым преломляющим углом и щелевого источника света, параллельного ребру бипризмы. Интерференционные полосы наблюдаются на экране, расположенном перпендикулярно к оси установки. Нулевая полоса получается в центре экрана – на оси (точнее, в плоскости симметрии) установки. Расстояние от источника до бипризмы равно a, от бипризмы до экрана b. В какую сторону и на какую величину x сместится нулевая интерференционная полоса, если щелевой источник света немного сместить в направлении, перпендикулярном к оси оптической системы, на величину h?

· От двух когерентных источников света S ₁ и S ₂ получена система интерференционных полос на экране AB, удаленном от источников на расстоянии a = 2 м. Во сколько раз изменится ширина интерференционных полос, если между источниками и экраном поместить собирающую линзу с фокусным расстоянием f = 25 см. Рассмотреть два случая: 1) расстояние линзы от источников равно 2 f = 50 см; 2) источники S ₁ и S ₂ находятся в фокальной плоскости линзы.

· В очень тонкой клиновидной пластинке в отраженном свете при нормальном падении наблюдаются интерференционные полосы. Расстояние между соседними темными полосами 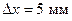. Зная, что длина световой волны равна l = 580 нм, а показатель преломления пластинки 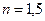, найти угол между гранями пластинки.

· Наблюдаются полосы равной толщины в воздушном клине между двумя плоскопараллельными стеклянными пластинками, образующими между собой очень малый угол. Клин освещается рассеянным светом. Наблюдение ведется невооруженным глазом с расстояния ясного зрения L = 25 см в направлении, перпендикулярном к поверхности клина, причем глаз может смещаться перпендикулярно к ребру клина. Оценить максимальное число интерференционных полос N, которое может видеть глаз в монохроматическом свете при таком способе наблюдения, если диаметр зрачка глаза d = 5 мм. Оценить степень монохроматичности света, необходимого для того, чтобы такое максимальное число полос могло наблюдаться.

· Полосы равной толщины, получающиеся в тонком стеклянном клине с показателем преломления 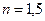при освещении рассеянным монохроматическим светом с длиной волны l = 500 нм, проектируются линзой на экран. Перед линзой помещена квадратная диафрагма со стороной d = 1 см и отстоящая от клина на расстоянии a = 50 см. Какой максимальный порядок интерференции N может при этом наблюдаться на экране? Главная оптическая ось проектирующей системы приблизительно перпендикулярна поверхности клина.

· При наблюдении колец Ньютона в отраженном свете (l_С = 450 нм) с помощью плоско-выпуклой линзы, положенной на плоскую пластинку, радиус третьего светлого кольца оказался равным 1,06 мм. После замены синего светофильтра на красный был измерен радиус пятого светлого кольца, оказавшийся равным 1,77. Найти радиус кривизны R линзы и длину волны l_К красного света.

8. Дифракция света

· Длины волн дуплета в излучении натрия равны l₁=589 нм и l₂=589,6 нм. Чему равно минимальное число щелей в дифракционной решетке, чтобы разрешить этот дуплет во втором порядке? в первом порядке?

· Поверхность Луны облучается пучком света, диаметр которого на выходе из лазера равен 0,5 см. Расходимость пучка чисто дифракционная, влиянием атмосферы пренебречь. Чему равен диаметр лазерного пучка при достижении поверхности Луны, если расстояние до Луны 386×10³ км, а длина волны лазерного излучения 632,8 нм?

· Вычислить радиус m -й зоны Френеля, если расстояние от источника до зонной пластинки равно a, а расстояние от пластинки до места наблюдения равно b. Длина волны l. 2) Найти радиус первой зоны, если a=b= 10 м, l=4500 Å.

· Плоская световая волна падает нормально на диафрагму с круглым отверстием, которое открывает первые N зон Френеля – для точки P на экране, отстоящем от диафрагмы на расстоянии b. Длина волны света равна l. Найти интенсивность света I ₀ перед диафрагмой, если известно распределение интенсивности света на экране I (r), где r ­ расстояние до точки P.

· Точечный источник света с длиной волны l=0,5 мкм расположен на расстоянии a= 100 см перед диафрагмой с круглым отверстием радиуса r = 1,0 мм. Найти расстояние b от диафрагмы до точки наблюдения, для которой число зон Френеля в отверстии составляет m =3.

· Между точечным источником света и экраном поместили диафрагму с круглым отверстием, радиус которого r можно менять. Расстояние от диафрагмы до источника и экрана равны a= 100 см и b= 125 см. Определить длину волны света, если максимум освещенности в центре дифракционной картины на экране наблюдается при r ₁=1,00 мм и следующий максимум при r ₂=1,29 мм.

· Плоская световая волна с l=640 нм и интенсивностью I ₀ падает нормально на круглое отверстие радиуса r =1,20 мм. Найти интенсивность в центре дифракционной картины на экране, отстоящем на расстоянии b= 1,50 м от отверстия.

· Плоская монохроматическая световая волна с интенсивностью I ₀ падает нормально на непрозрачный экран с круглым отверстием. Какова интенсивность света I за экраном в точке, для которой отверстие:

а) равно первой зоне Френеля;

б) внутренней половине первой зоны;

в) сделали равным первой зоне Френеля и затем закрыли его половину по диаметру?

· Монохроматическая плоская световая волна с интенсивностью I ₀ падает нормально на непрозрачный диск, закрывающий для точки наблюдения P первую зону Френеля. Какова стала интенсивность света I в точке P после того, как у диска удалили:

а) половину по диаметру;

б) половину внешней половины первой зоны Френеля по диаметру?

· Плоская световая волна с l=0,60 мкм и интенсивностью I ₀ падает нормально на большую стеклянную пластинку, профиль которой показан на рисунке. При какой высоте h уступа интенсивность света в точках, расположенных под ним, будет:

а) минимальна;

б) вдвое меньше I ₀ (потерями на отражения пренебречь).

· Плоская монохроматическая световая волна падает нормально на непрозрачную полуплоскость. На расстоянии b =100 см за ней находится экран. Найти с помощью спирали Корню:

а) отношение интенсивностей первого максимума и соседнего с ним минимума;

б) длину волны света, если расстояние между двумя первыми максимумами D x =0,63 мм.

· Плоская монохроматическая световая волна падает нормально на длинную прямоугольную щель, за которой на расстоянии b =60 см находится экран. Сначала ширину щели установили такой, что в середине дифракционной картины на экране наблюдался наиболее глубокий минимум. Раздвинув после этого щель на D h =0,70 мм, получили в центре картины следующий минимум. Найти длину волны света.

· Свет с длиной волны l падает нормально на длинную прямоугольную щель ширины b. Найти угловое распределение интенсивности света при фраунгоферовой дифракции, а также угловое положение минимумов.

· Монохроматический свет падает нормально на щель ширины b =11 мкм. За щелью находится тонкая линза с фокусным расстоянием f =150 мм, в фокальной плоскости которой расположен экран. Найти длину волны света, если расстояние между симметрично расположенными минимумами третьего порядка (на экране) равно x =50 мм.

· Монохроматический свет падает на отражательную дифракционную решетку с периодом d =1,0 мм под углом скольжения a₀=1,0°. Под углом скольжения a=3,0° образуется фраунгоферов максимум второго порядка. Найти длину волны света.

· Свет с длиной волны 535 нм падает нормально на дифракционную решетку. Найти ее период, если одному из фраунгоферовых максимумов соответствует угол дифракции 35° и наибольший порядок спектра равен пяти.

· Плоская световая волна длины l падает нормально на фазовую дифракционную решетку, профиль которой показан на рисунке. Решетка нанесена на стеклянной пластинке с показателем преломления n Найти глубину h штрихов, при которой интенсивность центрального фраунгоферова максимума равна нулю. Каков при этом угол дифракции, соответствующий первому максимуму?

· Свет, содержащий две спектральные линии с длинами волн 600,000 и 600,050 нм, падает нормально на дифракционную решетку ширины 10,0 мм. Под некоторым углом дифракции q эти линии оказались на пределе разрешения (по критерию Рэлея). Найти q.

· Свет падает нормально на дифракционную решетку ширины l =6,5 см, имеющую 200 штрихов на миллиметр. Исследуемый спектр содержит спектральную линию с l=670,8 нм, которая состоит из двух компонент, отличающихся на dl=0,015 нм. Найти:

а) в каком порядке спектра эти компоненты будут разрешены;

б) наименьшую разность длин волн, которую может разрешить эта решетка в области l»670 нм.

· Вычислить наименьшее расстояние между двумя точками на Луне, которое можно разрешить рефлектором с диаметром зеркала 5,0 м. Считать, что l=0,55 мкм.

· В фокальной плоскости объектива образуется дифракционное изображение удаленного точечного источника. Оценить, как изменится освещенность в центре этого изображения, если объектив заменить другим, с тем же фокусным расстоянием, но с диаметром вдвое большим.

· Определить минимальное увеличение зрительной трубы с диаметром объектива D =5,0 см, при котором разрешающая способность ее объектива будет полностью использована, если диаметр зрачка глаза d ₀=4,0 мм.

9. Оптика анизотропных сред

· Узкий пучок естественного света с длиной волны l=589 нм падает нормально на поверхность призмы Волластона, сделанной из исландского шпата, как показано на рисунке. Оптические оси обеих частей призмы взаимно перпендикулярны. Найти угол a между направлениями пучков за призмой, если угол q=30°.

· Требуется изготовить параллельную оптической оси кварцевую пластинку, толщина которой не превышала бы 0,5 мм. Найти максимальную толщину этой пластинки, при которой линейно поляризованный свет с l=589 нм после прохождения ее:

а) испытывает лишь поворот плоскости поляризации;

б) станет поляризованным по кругу.

· Белый естественный свет падает на систему из двух скрещенных поляризаторов, между которыми находится кварцевая пластинка, вырезанная параллельно оптической оси, толщиной 1,5 мм. Ось пластинки составляет угол 45° с плоскостями пропускания поляризаторов. Прошедший через эту систему свет разложили в спектр. Сколько темных полос будет наблюдаться в интервале длин волн 0,55–0,66 мкм? Разность показателей преломления необыкновенного и обыкновенного лучей в этом интервале длин волн считать равной 0,0090.

· Кристаллическая пластинка, вырезанная параллельно оптической оси, имеет толщину 0,25 мм и служит пластинкой в четверть волны для l=0,53 мкм. Для каких еще длин волн в области видимого спектра она будет также пластинкой в четверть волны? Считать, что для этих длин волн видимого спектра разность показателей преломления n_e-n_o =0,0090.

· Естественный монохроматический свет падает на систему из двух скрещенных поляризаторов, между которыми находится кварцевая пластинка, вырезанная перпендикулярно к оптической оси. Найти минимальную толщину пластинки, при которой эта система будет пропускать h=0,30 светового потока, если постоянная вращения кварца a=17 угл. град/мм.

· Свет проходит через систему из двух скрещенных поляризаторов, между которыми расположена кварцевая пластинка, вырезанная перпендикулярно к оптической оси. Определить минимальную толщину пластинки, при которой свет с длиной волны 436 нм будет полностью задерживаться этой системой, а свет с длиной волны 497 нм – пропускаться наполовину. Постоянная вращения кварца для этих длин волн равна соответственно 41,5 и 31,1 угл. град/мм.

· Ячейку Керра поместили между двумя скрещенными поляризаторами так, что направление электрического поля Е в конденсаторе образует угол 45° с плоскостями пропускания поляризаторов. Конденсатор имеет длину l =100 мм и заполнен нитробензолом. Через систему проходит свет с l=0,5 мкм. Имея в виду, что в данном случае постоянная Керра B = 2,2×10^-10 см/В², определить:

а) минимальную напряженность электрического поля Е в конденсаторе, при которой интенсивность света, прошедшего через эту систему, не будет зависеть от поворота заднего поляризатора;

б) число прерываний света в одну секунду, если на конденсатор подать синусоидальное напряжение с частотой n=10 МГц и амплитудным значением напряженности E_m =50 кВ/см. Постоянной Керра называется коэффициент B в формуле .

· Монохроматический плоскополяризованный свет с круговой частотой w проходит через вещество вдоль однородного магнитного поля с напряженностью Н. Найти разность показателей преломления для право- и левополяризованных по кругу компонент светового пучка, если постоянная Верде равна V.

· Трубка с бензолом длины l =26 см находится в продольном магнитном поле соленоида, расположенного между двумя поляризаторами. Угол между плоскостями пропускания поляризаторов равен 45°. Найти минимальную напряженность магнитного поля, при которой свет с длиной волны 589 нм будет проходить через эту систему только в одном направлении (оптический вентиль). Как будет вести себя этот оптический вентиль, если изменить направление данного магнитного поля на противоположное?

· Пучок естественного света интенсивности I ₀ падает на систему из двух скрещенных поляризаторов, между которыми находится трубка с некоторым оптически неактивным раствором в продольном магнитном поле напряженности H. Длина трубки l, линейный показатель поглощения раствора c и постоянная Верде V. Пренебрегая отражениями, найти интенсивность света, прошедшего через эту систему.

· Две поляризационные призмы с воздушной прослойкой изготовлены из исландского шпата. В одной призме оптическая ось перпендикулярна, в другой – параллельна плоскости падения (см. рис.). Опишите действие каждой призмы. Как будет поляризован проходящий свет? В каких пределах должен быть заключен угол a, чтобы из призмы выходил линейно поляризованный свет. Для исландского шпата n_o =1,658, n_e =1,486. Свет падает на грань призмы перпендикулярно.

· Какова должна быть наименьшая толщина d пластинки слюды, чтобы она могла служить в качестве пластинки в ¼ волны для света натрия, если для этого света показатели преломления волн, идущих перпендикулярно к пластинке, соответственно равны n ₁=1,5941, n ₂=1,5887?

· Найти наименьшую толщину d пластинки кварца, вырезанной параллельно оптической оси, чтобы падающий плоскополяризованный свет выходил поляризованным по кругу (n_e =1,5533, n_o =1,5442, l=5×10^{-5 см).}

· Два николя N ₁ и N ₂ повернуты один относительно другого на угол a; между ними помещен николь N ₃. На систему падает параллельный пучок неполяризованного света. Предполагая, что необыкновенный луч проходит через каждый николь без потерь, найти ориентацию николя N ₃ относительно николя N ₁, при которой интенсивность проходящего света максимальна. Определить интенсивность проходящего света в этих положениях, если интенсивность падающего света равна I ₀.

· На пластинку кварца, вырезанную параллельно оптической оси, нормально падает белый свет, поляризованный по кругу. За пластинкой поставлен поляроид, главное направление которого составляет угол 45° с осью пластинки. Прошедший свет попадает на щель спектрографа. Сколько темных полос k получится в спектре, если толщина кварцевой пластинки d =2 мм, n_e =1,55, n_o= 1,54. Падающий свет занимает интервал длин волн от 400 до 500 нм, в котором n_e–n_o= const.

Date: 2015-08-06; view: 3233; Нарушение авторских прав