
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Краткая теория. Из теории Максвелла следует, что световая волна является поперечной
|
|
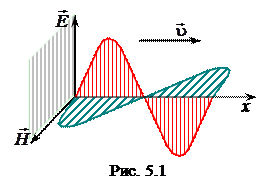 Из теории Максвелла следует, что световая волна является поперечной. Поперечность световых волн (как и любых других электромагнитных волн) выражается в том, что колебания векторов
Из теории Максвелла следует, что световая волна является поперечной. Поперечность световых волн (как и любых других электромагнитных волн) выражается в том, что колебания векторов 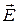 и
и 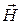 перпендикулярны направлению распространения волны (рис. 5.1). Плоская монохроматическая волна, распространяющаяся в вакууме вдоль оси x, описывается уравнениями:
перпендикулярны направлению распространения волны (рис. 5.1). Плоская монохроматическая волна, распространяющаяся в вакууме вдоль оси x, описывается уравнениями:
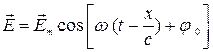 , ,
| (5.1) |
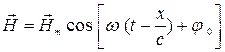 , ,
| (5.2) |
где 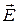 и
и 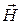 – текущее значение напряженности электрического и магнитного поля,
– текущее значение напряженности электрического и магнитного поля, 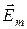 и
и 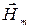 – амплитуды колебаний, w – частота колебаний,
– амплитуды колебаний, w – частота колебаний, 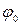 – начальная фаза колебаний.
– начальная фаза колебаний.
При взаимодействии света с веществом переменное электрической поле воздействует на отрицательно заряженные электроны атомов и молекул этого вещества, в то время как действие со стороны магнитного поля на заряженные частицы незначительно. Поэтому в процессах распространения света главную роль играет вектор 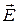 , и дальнейшем мы будем говорить только о нём.
, и дальнейшем мы будем говорить только о нём.
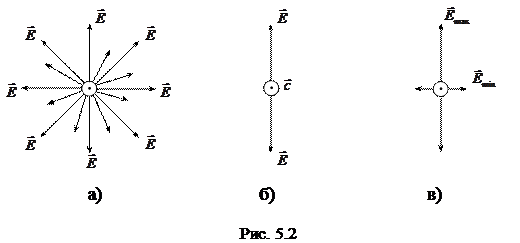
Большинство источников света состоит из огромного количества излучающих атомов, и поэтому в световом луче присутствует большое количество волн с различной пространственной ориентацией векторов 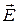 . Кроме того, эта ориентация беспорядочно меняется за чрезвычайно малые промежутки времени (рис. 5.2, а). Подобное излучение называется неполяризованным, или естественным светом. Свет, в котором направления колебаний вектора
. Кроме того, эта ориентация беспорядочно меняется за чрезвычайно малые промежутки времени (рис. 5.2, а). Подобное излучение называется неполяризованным, или естественным светом. Свет, в котором направления колебаний вектора 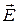 каким-либо образом упорядочены, называется поляризованным, а процесс получения поляризованного света – поляризацией. Если колебания вектора
каким-либо образом упорядочены, называется поляризованным, а процесс получения поляризованного света – поляризацией. Если колебания вектора 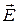 происходят в одной плоскости, то волна называется плоско-поляризованной или линейно-поляризованной (рис. 5.2, б). Частично поляризованным называется свет, в котором имеется преимущественное направление колебаний векторов
происходят в одной плоскости, то волна называется плоско-поляризованной или линейно-поляризованной (рис. 5.2, б). Частично поляризованным называется свет, в котором имеется преимущественное направление колебаний векторов 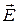 (рис. 5.2, в).
(рис. 5.2, в).
 |
Поляризация света наблюдается при прохождении света через анизотропные вещества. Основное свойство таких веществ заключается в том, что они могут пропускать световые волны лишь в строго определённой плоскости, которую называют плоскостью поляризации. Плоскость поляризации – это плоскость, проходящая через направление колебаний электрического вектора линейно поляризованной световой волны и направление распространения этой волны.
В настоящее время для получения и исследования поляризованного света применяют поляроиды. Они изготавливаются из очень мелких кристаллов турмалина или геропатита (сернокислого йод-хинина), нанесённых на прозрачную плёнку.
Рассмотрим следующий опыт. Возьмем два поляроида и источник света (рис. 5.3). Первый поляроид называется поляризатором, так как он поляризует свет. Его плоскостью поляризации является плоскость ППс. После прохождения через поляризатор вектор 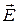 будет колебаться в этой плоскости. Вращая поляризатор вокруг направления светового пучка, мы не заметим никаких изменений в интенсивности прошедшего через него света. Подумайте почему? Анализ света на поляризацию делают с помощью второго поляроида, через который пропускают исследуемый свет. В этом случае второй поляроид называется анализатором, его плоскостью поляризации является плоскость ААс. Вращая анализатор, мы заметим, что интенсивность света будет максимальной, если плоскости ППс и ААс совпадают, и минимальной, если эти плоскости перпендикулярны. Если же эти плоскости составляют некоторый угол, интенсивность света будет принимать промежуточное значение.
будет колебаться в этой плоскости. Вращая поляризатор вокруг направления светового пучка, мы не заметим никаких изменений в интенсивности прошедшего через него света. Подумайте почему? Анализ света на поляризацию делают с помощью второго поляроида, через который пропускают исследуемый свет. В этом случае второй поляроид называется анализатором, его плоскостью поляризации является плоскость ААс. Вращая анализатор, мы заметим, что интенсивность света будет максимальной, если плоскости ППс и ААс совпадают, и минимальной, если эти плоскости перпендикулярны. Если же эти плоскости составляют некоторый угол, интенсивность света будет принимать промежуточное значение.
Найдем зависимость между интенсивностью света I и углом a. Обозначим амплитуду электрического вектора луча, прошедшего через поляризатор, буквой Е 0. Плоскость колебаний анализатора ААс повёрнута относительно плоскости колебаний поляризатора ППс на угол a (рис. 5.4). Разложим вектор 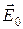 на составляющие: параллельную плоскости колебаний анализатора
на составляющие: параллельную плоскости колебаний анализатора 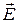 êê и перпендикулярную к ней
êê и перпендикулярную к ней 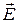 ^. Параллельная составляющая
^. Параллельная составляющая 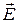 êê пройдёт через анализатор, а перпендикулярная
êê пройдёт через анализатор, а перпендикулярная 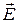 ^ – нет.
^ – нет.
 Из рис. 5.4 следует, что амплитуда световой волны за анализатором
Из рис. 5.4 следует, что амплитуда световой волны за анализатором
| Е êê = Е 0cosa. | (5.3) |
Интенсивность света равна средней энергии < W> световой волны, прошедшей сквозь единицу площади за единицу времени:
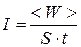 , ,
| (5.4) |
где S – площадь, по которой распределяется энергия; t – время.
Поскольку энергия света – это энергия электрического и магнитного полей, то её величина пропорциональна квадратам напряженностей этих полей:
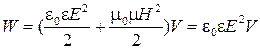 , ,
| (5.5) |
так как  .
.
Возводя равенство (5.3) в квадрат и умножая обе его части на e0e V/ 2, получим после деления на S и t следующее выражение для интенсивности света, прошедшего через анализатор:
| I = I 0 cos2a. | (5.6) |
Полученное равенство носит название закона Малюса: интенсивность света, прошедшего через анализатор, равна интенсивности света, прошедшего через поляризатор, умноженной на квадрат косинуса угла между плоскостями поляризации анализатора и поляризатора.
Заметим, что свет, прошедший через поляризатор, станет не только плоскополяризованным, но и уменьшит свою интенсивность в два раза. Если интенсивность естественного света считать одинаковой во всех направлениях, то интенсивность света за поляризатором будет
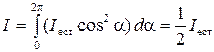 . .
| (5.7) |
Закон Малюса строго выполняется лишь для идеальных поляроидов. Чтобы установить, поляризовался свет полностью или частично, нужно найти степень поляризации Р, за меру которой принимают отношение
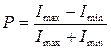 , ,
| (5.8) |
где I max и I min – наибольшая и наименьшая интенсивности света за анализатором, соответствующие напряжённостям Е max и Е min на рис. 5.2, в.
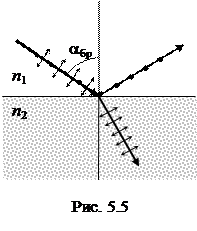 Явление поляризации можно также наблюдать при отражении или преломлении света на границе двух изотропных диэлектриков. При этом в отраженном луче будут преобладать колебания, перпендикулярные к плоскости падения (на рис. 5.5 они обозначены точками). Опытным путем было показано, что степень поляризации в отраженном луче зависит от величины угла падения, причем с возрастанием угла падения доля поляризованного света растет, и при определенном его значении отраженный свет оказывается полностью поляризованным. Брюстер установил, что величина этого угла полной поляризации зависит от относительного показателя преломления и определяется соотношением
Явление поляризации можно также наблюдать при отражении или преломлении света на границе двух изотропных диэлектриков. При этом в отраженном луче будут преобладать колебания, перпендикулярные к плоскости падения (на рис. 5.5 они обозначены точками). Опытным путем было показано, что степень поляризации в отраженном луче зависит от величины угла падения, причем с возрастанием угла падения доля поляризованного света растет, и при определенном его значении отраженный свет оказывается полностью поляризованным. Брюстер установил, что величина этого угла полной поляризации зависит от относительного показателя преломления и определяется соотношением
| tgaбр = n 2/ n 1. | (5.9) |
Соотношение носит название закона Брюстера, а угол aбр называют углом Брюстера. При дальнейшем увеличении угла падения степень поляризации света снова уменьшается. Таким образом, при угле падения, равном углу Брюстера, отраженный свет линейно поляризован в плоскости, перпендикулярной плоскости падения. Используя (5.9) и закон преломления, можно показать, что при падении под углом Брюстера отраженный и преломленный лучи составляют 90°. Проверьте это.
Простейшее физическое толкование закона Брюстера состоит в следующем. Электрическое поле падающей волны вызывает в диэлектрике колебания электронов. Направление этих колебаний совпадает с направлением электрического вектора преломленной волны. Эти колебания возбуждают на поверхности раздела отраженную волну, распространяющуюся от диэлектрика. Но линейно колеблющийся электрон не излучает в направлении своих колебаний. Таким образом, в отраженной волне колебания вектора 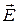 происходят только в плоскости, перпендикулярной плоскости падения.
происходят только в плоскости, перпендикулярной плоскости падения.
При падении света под углом Брюстера преломленный луч также поляризуется. В преломленном луче будут преобладать колебания, параллельные плоскости падения (на рис. 5.5 они обозначены стрелками). Поляризация преломленных лучей при этом угле падения будет максимальной, но далеко не полной. Если же подвергнуть преломленные лучи второму, третьему и т.д. преломлению, то степень поляризации возрастет. Поэтому для поляризации света можно использовать
8–10 пластинок (так называемая стопа Столетова). Прошедший через них свет окажется практически полностью поляризованным. Таким образом, эта стопа может служить поляризатором или анализатором. В нашей установке наборы из 2–12 пластин используются в качестве поляризатора.
Date: 2015-08-06; view: 805; Нарушение авторских прав