
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Фотоэффект и давление света
|
|
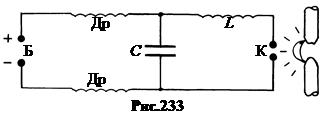 1. Открытие фотоэффекта. В 1887 г., работая с искровым колебательным контуром, Генрих Герц обнаружил, что искровой разряд между цинковыми электродами К облегчается, если освещать электроды светом от дугового фонаря (рис.233). Разряд в этом случае получается при меньшем напряжении питающей батареи Б.
1. Открытие фотоэффекта. В 1887 г., работая с искровым колебательным контуром, Генрих Герц обнаружил, что искровой разряд между цинковыми электродами К облегчается, если освещать электроды светом от дугового фонаря (рис.233). Разряд в этом случае получается при меньшем напряжении питающей батареи Б.
 Открытое явление стали называть фотоэффектом. В 1888 году Вильгельм Гальвакс установил, что под действием УФ света металлы теряют отрицательный электрический заряд.
Открытое явление стали называть фотоэффектом. В 1888 году Вильгельм Гальвакс установил, что под действием УФ света металлы теряют отрицательный электрический заряд.
Наиболее обстоятельно исследовал фотоэффект в 1888-1890 годах Александр Столетов. Главной частью установки Столетова был сетчатый конденсатор, передней обкладкой которого была латунная сетка С, а задней – цинковая пластина Zn (рис.234). Свет от дугового фонаря Д проходил сквозь сетку и падал на пластину. Наличие фотоэффекта регистрировалось гальванометром Г. В результате выполненных измерений Столетов установил:
а. Свет уносит с металлов отрицательный, но не уносит положительный заряд;
б. Чем короче длина волны света, тем эффективнее его разряжающее действие.
В 1898 г. Джозеф Томсон и Филипп Ленард измерили удельный заряд частиц, выбиваемых светом. Ими оказались электроны. Позднее выяснилось, что вырванный из атома вещества электрон не всегда покидает кристаллическую решётку. Поэтому стали различать внешний фотоэффект, когда электроны покидают вещество, и внутренний фотоэффект, когда электроны остаются в веществе. Внешний фотоэффект наблюдается обычно при освещении металлов, внутренний – в диэлектриках и полупроводниках.
2. Законы внешнего фотоэффекта. После открытия фотоэффекта возникли вопросы: от чего зависит кинетическая энергия фотоэлектронов, от интенсивности света или от частоты? От чего зависит количество выбитых электронов? Каково влияние материала освещаемого электрода? Детальные исследования Ленарда и других физиков, выполненные в вакууме, позволили установить следующее:
а. Электроны выбиваются светом, длина волны которого меньше некоторого предельного для данного вещества значения λ max. При λ > λ max электроны не выбиваются. Предельное значение λ max называют красной границей фотоэффекта для данного вещества.
б. Число N выбитых электронов пропорционально интенсивности I падающего света, 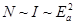 . Здесь E a – амплитуда напряжённости электрического поля световой волны.
. Здесь E a – амплитуда напряжённости электрического поля световой волны.
в. Кинетическая энергия выбитых электронов не зависит от интенсивности падающего света. Она пропорциональна его частоте ν. E кин = mυ 2 ç 2 ~ ν.
3. Трудности классической физики. Как и тепловое излучение, закономерности фотоэффекта не удаётся объяснить в рамках волновой модели света. Так, в волновой теории освещаемый электрон под действием ЭМ волны должен совершать вынужденные колебания, амплитуда которых пропорциональна амплитуде волны Е а. При достаточно большом значении E a кинетическая энергия электрона может превысить энергию связи, в результате электрон вылетит наружу. Так как 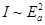 , то энергия фотоэлектронов должна быть тем больше, чем больше интенсивность света. В этом случае фотоэффект должен наблюдаться при освещении светом с любой длиной волны λ, лишь бы свет был достаточно интенсивным.
, то энергия фотоэлектронов должна быть тем больше, чем больше интенсивность света. В этом случае фотоэффект должен наблюдаться при освещении светом с любой длиной волны λ, лишь бы свет был достаточно интенсивным.
В рамках волновой модели необъяснима красная граница фотоэффекта и то, что энергия фотоэлектронов пропорциональна частоте света.
Количество выбитых электронов должно зависеть, казалось бы, лишь от того, какова концентрация раскачиваемых светом электронов на поверхности металла, то есть зависеть от вещества. В действительности число выбитых электронов пропорционально интенсивности света, а от свойств вещества зависит красная граница фотоэффекта.
4. Квантовая теория фотоэффекта. Эти трудности преодолел Эйнштейн в 1905 г. в рамках квантовой гипотезы Планка. Эйнштейн развил гипотезу Планка утверждением, что свет не только испускается квантами (Планк), но и существует и поглощается веществом так же квантами. Если Планк приписал свойство квантованности только физическому процессу излучения света атомом, то Эйнштейн сделал понятие квантованности более фундаментальным. Он определил его как постоянное свойство физического объекта – ЭМ излучения. Позднее выяснилось, что свойство квантованности присуще всей материи.
Поскольку при фотоэффекте квант электромагнитного излучения – фотон должен поглощаться полностью, то закон сохранения энергии для единичного акта выбивания электрона принимает вид:  . Формула Эйнштейна, 1905 (30.1)
. Формула Эйнштейна, 1905 (30.1)
Здесь hn – энергия поглощаемого фотона, mυ 2 ç 2 – кинетическая энергия выбиваемого электрона. Если электрон выбивается из конденсированной среды – твёрдого тела или жидкости, то величина А есть работа выхода электрона из этой среды. При выбивании электронов из единичных атомов в газах А есть энергия ионизации атомов.
Квантовая теория фотоэффекта объясняет все его закономерности.
а. Красная граница обусловлена тем, что фотоэффект происходит лишь тогда, когда энергия фотонов больше или равна работе выхода электронов.
hn ≥ A, Þ 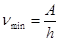 ,
, 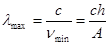 . (30.2)
. (30.2)
| Таблица 30.1 | |||
| Металл | l max, нм | Металл | λ max, нм |
| Цезий Cs | Цинк Zn | ||
| Калий K | Вольфрам W | ||
| Натрий Na | Серебро Ag | ||
| Литий Li | Платина Pt |
Красная граница фотоэффекта определяется свойствами вещества. У щелочных металлов она находится в видимой области спектра, у остальных – в ультрафиолетовой (табл.30.1).
б. Пропорциональность числа выбитых электронов интенсивности света. Если свет есть поток фотонов, то увеличение интенсивности света соответствует увеличению числа фотонов, I = nhn, где n – число фотонов, проходящих через единичную площадку в единицу времени. Чем больше интенсивность света, тем больше в пучке фотонов, тем больше выбитых электронов.
Правда, это справедливо лишь при условии, что число выбивающих фотонов меньше числа вакантных электронов в поверхности металла. Но при обычных, не больших интенсивностях света это условие выполняется.
в. Пропорциональность кинетической энергии фотоэлектронов частоте падающего света автоматически вытекает из формулы Эйнштейна.
5. Опытная проверка формулы Эйнштейна была сделана Милликеном в 1916 г. При этом выяснилось, что красная граница сильно зависит от наличия в металле примесей. Растворённые в металлах газы облегчают выход электронов, смещая красную границу в область более длинных волн. Поэтому точные исследования фотоэффекта возможны только в вакууме.
В 1928 г. Пётр Лукирский и Сергей Прилежаев продолжили изучение фотоэффекта на улучшенной установке. Вместо открытого конденсатора Милликена они использовали замкнутый сферический конденсатор, позволявший собрать все электроны.
Все опыты подтвердили формулу Эйнштейна.
6. Многофотонный фотоэффект. Из квантовой структуры света вытекает принципиальная возможность существования наряду с однофотонным фотоэффектом (1 фотон → 1 электрон) многофотонного фотоэффекта (n фотонов → 1 электрон). То есть электрон может вырываться из металла за счёт энергии нескольких одновременно поглощенных фотонов.
В этом случае должно происходить смещение красной границы фотоэффекта в область длинных волн. При одновременном поглощении n одинаковых фотонов с энергиями hn формула Эйнштейна принимает вид: 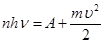 ,
, 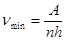 .
. 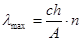 . (30.3)
. (30.3)
Предельная длина волны увеличивается в n раз.
Многофотонный фотоэффект удалось наблюдать лишь в 60-е годы 20 в. с помощью интенсивных лазерных пучков. При этом n достигало 5.
7. Давление света в электромагнитной теории. Независимо от того, выбивает электрон падающий на вещество свет или нет, свет должен создавать на освещаемую поверхность давление. Идея светового давления была высказана ещё Кеплером в 17 в. для объяснения кометных хвостов. В корпускулярной модели Ньютона давление света вытекало с очевидностью как результат соударения световых корпускул с освещаемой поверхностью. Каждая корпускула, ударяясь о поверхность, должна сообщать ей импульс. Однако опытом факт светового давления не подтверждался. Нельзя было даже теоретически оценить величину предполагаемого давления.
 С появлением эфирной волновой модели света вопрос о давлении света потерял свою актуальность. Он мог рассматриваться лишь как способ подтверждения корпускулярной (есть давление) или волновой (нет давления) модели света.
С появлением эфирной волновой модели света вопрос о давлении света потерял свою актуальность. Он мог рассматриваться лишь как способ подтверждения корпускулярной (есть давление) или волновой (нет давления) модели света.
Проблема светового давления снова возродилась после 1873г., когда Максвелл построил электродинамику. Из анализа колебаний под действием ЭМ поля световой волны оптического электрона в атоме получается, что ЭМ волна, падающая на поверхность тела, должна оказывать на неё давление, равное p = W 0(1 + ρ), (30.4)
где W 0 – плотность энергии волны, ρ – коэффициент отражения по интенсивности.
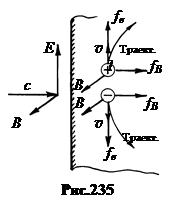
Качественно механизм возникновения светового давления можно уяснить из рис.235. Сила давления направлена вдоль светового луча и не зависит от знака электрических зарядов, движущихся в веществе.
Под действием силы 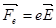 , действующего со стороны электрического поля волны на электрические заряды, разноимённые заряды движутся в противоположных направлениях. Но магнитная сила Лоренца
, действующего со стороны электрического поля волны на электрические заряды, разноимённые заряды движутся в противоположных направлениях. Но магнитная сила Лоренца 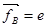 [
[ 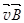 ], действующая на заряды со стороны магнитного поля волны
], действующая на заряды со стороны магнитного поля волны 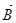 , направлена в сторону распространения луча. В результате заряды движутся по кривым траекториям вглубь вещества. Сталкиваясь с узлами кристаллической решётки, они передают ей импульс. Поэтому решётка испытывает давление света.
, направлена в сторону распространения луча. В результате заряды движутся по кривым траекториям вглубь вещества. Сталкиваясь с узлами кристаллической решётки, они передают ей импульс. Поэтому решётка испытывает давление света.
 8. Опыты Лебедева. Величина давления света очень мала. По вычислениям Максвелла солнечные лучи на Земле создают давление около 4·10–6 Па. Поэтому экспериментальное измерение давления и по сей день остаётся сложной задачей. Впервые её успешно решил в 1899-900 годах Пётр Лебедев. В результате серии блестящих экспериментов он не только подтвердил факт давления света, но и измерил его.
8. Опыты Лебедева. Величина давления света очень мала. По вычислениям Максвелла солнечные лучи на Земле создают давление около 4·10–6 Па. Поэтому экспериментальное измерение давления и по сей день остаётся сложной задачей. Впервые её успешно решил в 1899-900 годах Пётр Лебедев. В результате серии блестящих экспериментов он не только подтвердил факт давления света, но и измерил его.
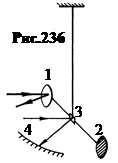
В основу установки были положены крутильные весы (рис.236). Свет направлялся на одно из крылышек 1 или 2 лёгкой вертушки, а её поворот регистрировался по шкале 4 с помощью зайчика, который отбрасывался зеркальцем 3. Главная трудность опытов состояла в устранении конвективных потоков газа и радиометрического эффекта.
а. Конвективные потоки закручивают подвес при несколько наклонном положении крылышка. Их влияние ослаблялось созданием вакуума и тем, что свет направлялся на крылышко поочерёдно с разных сторон. В одном случае сила конвекции добавлялась к силе светового давления, в другом – вычиталась из него.
б. Радиометрический эффект возникает вследствие разности температур освещённой и неосвещённой сторон крылышка. От более тёплой стороны молекулы воздуха, которые там всё – равно есть, отражаются с большей скоростью, и потому их отдача больше.
С целью устранения радиометрического эффекта крылышки делались тонкими (0,01¸0,1 мм), благодаря чему температура их сторон отличалась незначительно.
Параметры установки: диаметр крылышек 5 мм, их толщина – от 0,01 до 0,1 мм, материал – платина, алюминий, никель, слюда. В итоге измерений Лебедев показал, что с относительной погрешностью опыта до 20% формула давления Максвелла подтверждается.
9. Давление света в квантовой теории. Если представить энергию фотона hν по формуле Эйнштейна hν = mc 2, где m – масса фотона, то импульс фотона есть mc = hνçc. При взаимодействии фотона с поверхностью она получает от него импульс 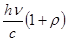 . (30.5)
. (30.5)
Для единичного фотона может быть только 2 случая: коэффициент отражения ρ = 0, неупругое взаимодействие, и ρ = 1, абсолютно упругое взаимодействие. При ρ = 0 стенка поглощает фотон и получает импульс hνçc. При ρ = 1 стенка отражает фотон и получает удвоенный импульс 2 hνçc. Все промежуточные значения 0 < ρ < 1 реализуются в статистике. То есть ρ равно доле отражённых фотонов.
Пусть N – число движущихся фотонов в единице объёма излучения. За время dt на площадку S попадает N ·(cdt)· S фотонов. Из них доля ρ отразится, а 1 – ρ поглотится.
Поглощённые и отраженные фотоны передадут стенке соответственно импульсы
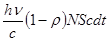 , и
, и 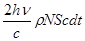 . (30.6, 30.7)
. (30.6, 30.7)
Суммарный импульс за время dt 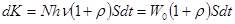 . (30.8)
. (30.8)
Отсюда находится давление света на стенку. 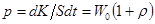 . (30.9)
. (30.9)
Формула совпадает с выражением (30.4).
9. Давление света существенно в двух противоположных по масштабу областях явлений – астрономических и атомарных. В космосе давление света наряду с давлением газа обеспечивает стабильность звёзд, противодействуя силам гравитационного сжатия. Оно существенно также для динамики межзвёздного газа.
К атомарным проявлениям давления света относится световая отдача, которую испытывает возбуждённый атом при испускании фотона или ядро при испускании g - кванта.
Date: 2015-08-06; view: 2004; Нарушение авторских прав