Теория относительности

1. Постулаты теории относительности. В 1905 г. Эйнштейн сформулировал два постулата, выделенные им как бесспорные следствия из всего накопленного опыта.

а. Все явления природы в инерциальных системах отсчёта протекают тождественно;

б. Скорость света в пустоте постоянна и не зависит от скорости движения источника.

Первый постулат называют специальным принципом относительности. По сравнению с принципом относительности Галилея он гораздо сильнее, поскольку устанавливает тождественность протекания в инерциальных системах не только механических, но всех возможных в природе физических процессов.

Эйнштейн показал, что для установления метрики пространства и времени в данной системе отсчёта кроме правил измерения длин и времени в данной точке пространства нужно дать ещё определение одновременности в разных точках. Как средство для её определения Эйнштейн берёт световой сигнал. Часы в точке А, по определению, синхронны с часами в точке В, если световой сигнал, выпущенный из А в момент времени t ₁(А) и вернувшийся после отражения в точку А после отражения в В в момент t ₂(A), отразился в точке В в момент t (B) = [ t ₁(A) + t ₂(A)] ç 2. Отсюда следует, что события могут быть одновременными в разных точках не вообще, а в определённой системе отсчёта с установленной метрикой пространства - времени.

2. Преобразования Лоренца. Эйнштейн показал, что преобразования, введённые Лоренцем в его электродинамике и рассматривавшиеся им как формально – вычислительный приём, имеют на само деле универсальное значение и являются реальными преобразованиями пространственных и временных отсчётов при переходе от одной системы отсчёта к другой. Они вытекают из основных постулатов теории относительности.

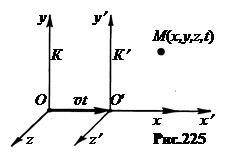
Пусть в инерциальной системе отсчёта К есть точка М с координатами x, y, z. Время в этой точке в системе К есть t.

Относительно системы К прямолинейно и равномерно вдоль осей ОХ и О¢Х¢ движется система К¢ со скоростью v (рис.225).

Формулы перехода от пространственно – временных координат в системе К к координатам в системе К¢ и обратно (преобразования Лоренца) имеют вид:

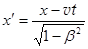Из К в К ´: , y ´ = y, z ´ = z, 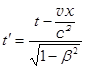. (28.1-а)

Из К´ в К: 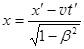, y = y ´, z = z ´, 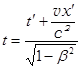. (28.1-б)

Здесь β =v/с. В теории Эйнштейна оба времени t и t¢ рассматриваются как объективные физические реальности, присущие определённым системам отсчёта. Пространственные и временные промежутки теряют абсолютность, которая присуща им в ньютоновом пространстве – времени.

3. Изменение временных интервалов. Пусть в системе К в определённой точке М с координатами x, y, z последовательно в моменты времени t ₁ и t ₂ происходят две вспышки. Промежуток времени между ними D t = t ₂ – t ₁. Вопрос: какой интервал времени D t¢ пройдёт между вспышками в системе К ’? Из преобразований Лоренца (28.18-а) имеем:

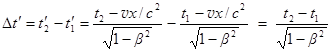. Отсюда 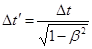. (28.2)

В любой системе К¢, движущейся относительно К с некоторой скоростью v, время Δ t¢ > Δ t (релятивистский корень в знаменателе меньше единицы). Следовательно, продолжительность физического явления минимальна в собственной системе отсчёта.

Если физический объект, в котором протекает процесс, движется относительно наблюдателя с некоторой скоростью v, то продолжительность процесса по часам наблюдателя в 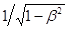раз больше продолжительности процесса в собственной системе отсчёта объекта. Например, время жизни нестабильных элементарных частиц в лабораторной системе отсчёта тем больше, чем с большей скоростью они движутся относительно лаборатории.

4. Сокращение размеров движущихся тел. Пусть в системе К' вдоль оси О'Х' покоится стержень длиной l' = x' ₂ – x' ₁, где x' ₁ и x' ₂ – координаты концов стержня, измеренные в системе К'. Вопрос: какова длина l и координаты концов этого стержня в системе К, измеренные в момент времени t? Из преобразований Лоренца (28.1а)

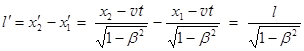. Отсюда: . (28.3)

В системе отсчёта, относительно которой стержень движется, длина его меньше по сравнению с той системой, где он покоится. Максимальную длину стержень имеет в собственной системе отсчёта.

5. Преобразование скоростей в теории относительности. Пусть относительно системы К' тело движется со скоростью u' = d x'ç d t'.

Вопрос: с какой скоростью движется это тело в системе К?

Очевидно, u = d xç d t = (d xç d t') ç (d tç d t'). Вычислим производные из преобразований Лоренца (28.1-б). , .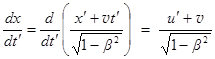

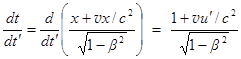Подставляем и получим 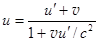, , 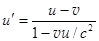(28.3)

Рассмотрим частные случаи.

а. Пусть в системе К ´ распространяется световой сигнал со скоростью u ´ = c. Скорость этого сигнала в системе К есть .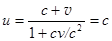

Скорость света во всех ИСО одинакова и равна с.

б. Пусть система К ´ движется со скоростью v = с, и в ней в направлении движения испускается свет со скоростью u ´ = c. Скорость светового импульса в системе К есть

.

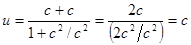Скорость света во всех ИСО одинакова и не зависит от скорости движения ИСО. Преобразования скоростей удовлетворяют второму постулату Эйнштейна.

6. Толкование теорией относительности опыта Физо. Если свет распространяется в оптической среде с показателем преломления n, и эта среда покоится в системе отсчёта К ’, то скорость света в К ’ есть u ´ = cçn.

В опытах Физо К ' - это система отсчёта, связанная с водой. Поэтому u ´ = c/n – это скорость света относительно воды.

Скорость света в системе К, относительно которой К ´ (вода) движется со скоростью v, есть 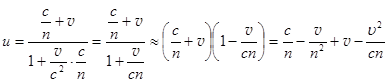. (28.4)

Последнее слагаемое много меньше предыдущих. Действительно, при n = 1,33, v = 7 м/с, получаем из (28.4): u = 2,25×10⁸ – 3,94 + 7 – 1,2×10^–7. Если последним слагаемым пренебречь, то формула принимает вид: 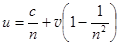. (28.5)

Именно такую зависимость показали опыты по схеме Физо.

7. Толкование теорией относительности отсутствие эфирного ветра в опытах Майкельсона. Как следовало из рассуждений Майкельсона, время t ₂ распространения светового импульса в плече, ориентированном вдоль скорости орбитального движения Земли (формула 27.8), больше времени t ₁ распространения света в плече поперёк скорости (формула 27.7).

Но если учесть релятивистское сокращение толщины слоя эфира в продольном плече, то путь светового импульса будет не 2 L, а 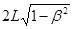. Тогда время t ₂ распространения света в продольном луче определяется не формулой (27.8), а формулой:

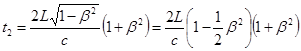. (28.6)

Используя t ₁ из формулы (27.7), получаем разность времён

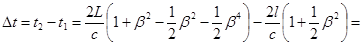
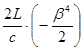. (28.7)

Количество N сместившихся при повороте полос (формула 27.10) принимает вид:

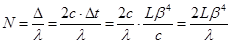. (28.8)

Орбитальная скорость Земли v = 3×10⁸ м / с, l = 589×10^–9 м, L = 11 м. Отсюда N = 2∙11 (3∙10⁴ ç 3∙10⁸)⁴ ç 589∙10^–9 = 3·10^–9. Смещение интерференционной полосы на одну миллиардную её ширины вряд ли когда-либо удастся измерить.

8. Эффект Допплера. В 1842 г. Кристиан Допплер теоретически обосновал зависимость частоты колебаний, воспринимаемых наблюдателем, от скорости и направления движения наблюдателя относительно источника колебаний или источника относительно наблюдателя.

Применительно к звуковым волнам, при относительном движении источника и приёмника звука вдоль соединяющей их прямой частота ν регистрируемого приёмником звука связана с частотой n ₀ источника соотношением:

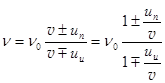. Акустическая формула Допплера, 1842 (28.9)

Здесь v – скорость звука в среде, u _и, u _п – скорость движения относительно среды источника и приёмника. Верхний знак в формуле соответствует сближению источника с приёмником, нижний – их взаимному удалению.

В оптике ситуация отличается. С упразднением абсолютного эфира исчезла та система отсчёта, относительно которой можно было измерять скорости источника и приёмника. Поэтому из трёх скоростей в акустической формуле v, u _и, u _п в оптической формуле Допплера остаются лишь две. Это скорость света с и скорость сближения (или удаления) источника и приёмника. А сама формула принимает вид:

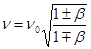. Оптическая формула продольного эффекта Допплера (28.10)

Здесь β = vçс. Верхний знак соответствует сближению, нижний – удалению.

Из теории относительности следует, что кроме продольного эффекта в оптике должен наблюдаться поперечный эффект. Если наблюдатель неподвижен, а вокруг него движется по окружности источник, излучающий волну с частотой n ₀, то воспринимаемая наблюдателем частота определяется формулой:

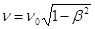. Оптическая формула поперечного эффекта Допплера (28.11)

Если продольный эффект Допплера определяется, в основном, тем, что изменяется число волн, укладывающихся на пути распространения между источником и приёмником, то поперечный эффект обусловлен разным ходом времени в системах отсчёта источника и наблюдателя. Поперечный эффект является эффектом второго порядка малости, поэтому наблюдать его труднее, чем продольный.

9. Опыты Белопольского. Первым экспериментально исследовал в лаборатории продольный эффект Допплера Аристах Белопольский в 1900 г. Для усиления эффекта Белопольский увеличил скорость движения источника за счёт многократного отражения от движущихся зеркал.

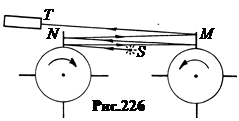Схема установки показана на рис.226. Зеркалами являлись радиальные лопасти двух колёс, вращающихся в противоположных направлениях. Между зеркалами помещался источник света S. Расстояние от источника света S по ходу движения луча до трубы спектрографа составляет x + 2 nx + a, где x = SN = SM, n – число отражений, а – расстояние от колеса N до трубы спектрографа T.

При сближении или удалении зеркал с линейной скоростью v расстояние от источника S до спектрографа Т изменяется со скоростью

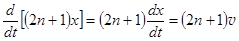. (28.12)

Максимальная скорость сближения, достигнутая Белопольским, составляла 2 nv = 670 м/с. Результаты опытов с точностью до 5% соответствовали формуле (28.10).

10. Поперечный эффект был подтверждён экспериментально лишь в 1938 г. в опытах с каналовыми лучами. Измерялась частота излучения атомов водорода, двигавшихся со скоростью около 2000 км/с. Смещение спектральных линий в спектрографе было около 0,00011 нм.

Заметим, что в отличие от продольного эффекта изменение частоты в поперечном эффекте происходит всегда в длинноволновую область спектра. Это чисто релятивистский эффект.

11. Применение эффекта Допплера наиболее плодотворно в астрофизике для определения скоростей движения светил вдоль луча (лучевые скорости), для изучения тесных двойных звёзд, для определения скоростей вращения Солнца и планет.

По допплеровскому уширению спектральных линий методами спектроскопии определяются тепловые скорости движения атомов и ионов в светящихся газах небесных тел, а по их значениям - температуры этих тел.

12. Релятивистская механика. Релятивистскими называются физические явления, протекающие в движущихся системах отсчёта, скорость движения υ которых соизмерима со скоростью света с в вакууме. Требование инвариантности энергии и импульса тел по отношению к преобразованиям Лоренца приводит к изменению выражений этих величин. Приведём без обсуждения несколько формул.

а. Релятивистская масса 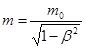, (28.13)

где m ₀ – масса покоя (т.е. масса тел в ИСО, связанной с самим телом);

б. Энергия покоя E ₀ = m ₀ c ²; (28.14)

в. Релятивистская энергия Е = mc ²; (28.15)

г. Релятивистская кинетическая энергия

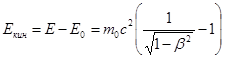; (28.16)

д. Релятивистский импульс 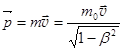. (28.17)

Все эти выражения при малых скоростях, когда vçс → 0, переходят в формулы классической механики.

Date: 2015-08-06; view: 561; Нарушение авторских прав