Завдання №3

Знайти стаціонарні точки динамічної системи

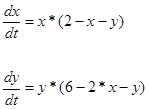(2.3.0)

та дослідити їх стійкість в лінійному наближенні.

Рішення:

1. Положення рівноваги вихідної динамічної системи (стаціонарні точки динамічної системи) визначається наступними умовами:

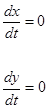
звідкіля маємо систему рівнянь рівноваги

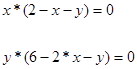(2.3.2)

Рішення системи рівнянь рівноваги (2.3.2)

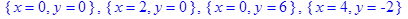(2.3.3)

2. Для дослідження стійкості кожного з отриманих рішень, складаємо системи першого наближення в околицях точок рівноваги за допомогою розкладення в ряд Тейлора. Формула Тейлора для функції двох змінних x, y у першому наближенні (тільки рівень 1 похідних) для функції 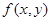в околицях точки x₀, y₀ має наступний вигляд [7]:

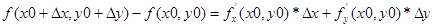(2.3.4)

Побудову систем рівнянь першого наближення системи (2.3.2)

6. Використовуючи отримані результати (2.3.5), (2.3.6), дослідження стійкості рішення для 4‑х пар коренів проводимо в наступній послідовності

6.1. 1 пара коренів – x=0, y=0

Cистема характеристичних рівнянь 1‑го наближення ряду Тейлора відносно точки (x=0, y=0) має вигляд:

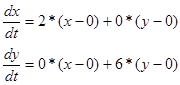
Для знаходження умов стійкості будуємо характеристичну матрицю:

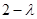
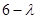
Звідки характеристичне рівняння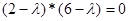

Корені рішення цього рівняння 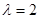та 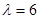є дійсні та мають однакові знаки, що відповідає стійкості рішення рівноваги [5] в точці (x=0, y=0).

Пара коренів – x=2, y=0

Cистема характеристичних рівнянь 1‑го наближення ряду Тейлора відносно точки (x=2, y=0) має вигляд:

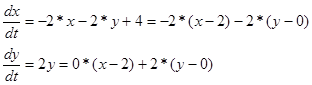
Виконуючи заміну змінних в системі () на

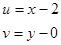
отримуємо модифіковану систему рівнянь:

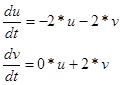
Для знаходження умов стійкості будуємо характеристичну матрицю:

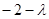
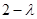
Звідки характеристичне рівняння

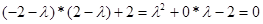
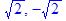
Корені рішення цього рівняння та 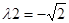є дійсні та мають різні знаки, що відповідає нестійкості рішення рівноваги [5] в точці (x=2, y=0).

3 пара коренів – x=4, y=-2

Cистема характеристичних рівнянь 1‑го наближення ряду Тейлора відносно точки (x=0, y=6) має вигляд:

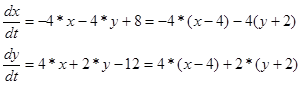
Виконуючи заміну змінних в системі () на

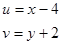
отримуємо модифіковану систему рівнянь:

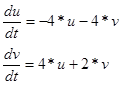
Для знаходження умов стійкості будуємо характеристичну матрицю:

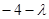
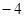
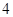
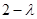
Звідки характеристичне рівняння

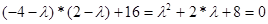
Вирішуємо рівняння () в пакеті MAPLE7

> solve (L*L+2*L+8);

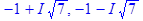
Корені рішення цього рівняння 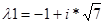та 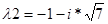є комплексні та мають однакові негативні знаки при дійсній частині, що відповідає стійкості рішення рівноваги [5] в точці (x=4, y=-2).

Пара коренів – x=0, y=6

Cистема характеристичних рівнянь 1‑го наближення ряду Тейлора відносно точки (x=4, y=-2) має вигляд:

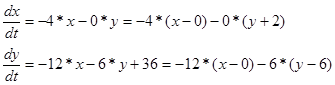
Виконуючи заміну змінних в системі () на

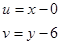отримуємо модифіковану систему рівнянь: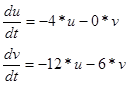

Для знаходження умов стійкості будуємо характеристичну матрицю:

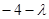
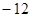
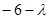
Звідки характеристичне рівняння

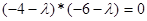
Корені рішення цього рівняння 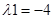та 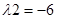є дійсними та мають знак (–) при дійсній частині, що відповідає асимптотичній стійкості рішення рівноваги [5] в точці (x=4, y=-2).