Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Завдання №2. Попит D та пропозиція S як функції змінної в часі ціни p=F(t) та її похідних задаються виразами
|
|
Попит D та пропозиція S як функції змінної в часі ціни p=F(t) та її похідних задаються виразами
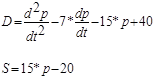(2.2.0)
Знайти стаціонарну ціну рівноваги попиту та пропозиції pD=S(t) – при умові D=S – вирівнювання попиту та пропозиції, як функцію часу, та з’ясувати чи вона є стійкою (оцінити рівень динаміки похідної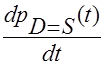 
).
Рішення:
1. Якщо попит D та пропозиція S є функціями ціни p(t) та її першої та другої похідних 
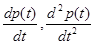, то їх рівняння в загальному вигляді можна представити наступним чином [1]:
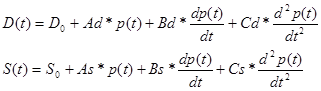(2.2.1)
2. В умовах пошуку точок рівноваги попиту та пропозиції:
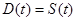(2.2.2)
рівняння (2.2.1), віднімаючи перше від другого, перетворюємо у наступне рівняння
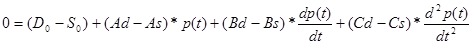(2.2.3)
яке має наступні початкові умови:
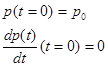(2.2.4)
Загальний розв’язок рівнянь (2.2.1) – (2.2.4) має вигляд [1]:
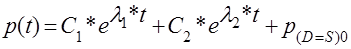(2.2.5)
де С1 та С2 – довільні сталі;
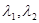– корені характеристичного рівняння:
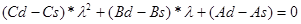(2.2.6)
Після вирішення рівняння (2.2.6), отримані 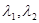– корені характеристичного рівняння в рівнянні (2.2.5) характеризують стаціонарність рівноважної ціни p(t) наступним чином:
1) Якщо обидва корені 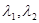– є дійсними від’ємними або комплексними з від’ємною дійсною частиною, то рівняння (2.2.5) перетворюється до вигляду:
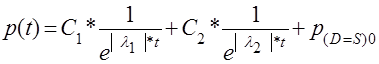(2.2.7)
та з наростанням t рівноважна ціна p(t) буде прямувати до ціни рівноваги попиту D та S – PD=S, оскільки 1 та другий член рівняння (2.2.7) будуть наближатися до нуля.
2) Якщо обидва корені 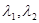– є дійсними позитивними, або один з них має позитивний знак, або комплексними з позитивною дійсною частиною, то згідно рівнянь (2.2.5), (2.2.7) з наростанням t рівноважна ціна p(t) буде віддалятися від до ціни рівноваги попиту D та S – PD=S, оскільки або перший, або другий член рівняння (2.2.5) будуть наближатися до 
.
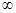3. В точці рівноваги попиту та пропозиції D=S, рівняння (2.2.0) перетворюються в наступне диференційне рівняння другого порядку похідних:
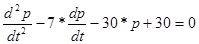(2.2.8)
Для пошуку точок стаціонарної ціни рівноваги pD=S враховуємо умови дорівнювання нулю першої та другої похідної в цих точках:
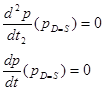(2.2.9)
тоді рівняння (2.2.8) перетворюється до вигляду, який дозволяє розрахувати значення стаціонарної ціни рівноваги попиту та прозиції:
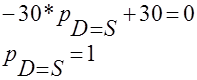(2.2.10)
Для рівняння (2.2.8) характеристичне рівняння має наступний вигляд:
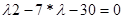(2.2.11)
а корені його рішення,
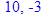
Оскільки корені характеристичного рівняння (2.2.11)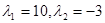 
дійсні та мають різні знаки – рішення рівняння (2.2.10) є нестійким.
Date: 2015-07-27; view: 313; Нарушение авторских прав