
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лабораторная работа № 8
|
|
по дисциплине
«ТЕХНИЧЕСКАЯ МЕХАНИКА»
для специальностей:
150203 «Сварочное производство»
190604 «Техническое обслуживание и ремонт автотранспорта»
190701 «Организация перевозок и управление на транспорте»
ЦЕЛЬ РАБОТЫ
Теоретическое и опытное определение осадки цилиндрической винтовой пружины и вычисление напряжений в витках.
ОБОРУДОВАНИЕ
1. Пружина сжатия винтовая цилиндрическая
2. Приспособление для сжатия пружин
3. Штангенциркуль
4. Линейка
ХАРАКТЕРИСТИКА ПРУЖИНЫ
Тип: пружина сжатия винтовая цилиндрическая.
Средний диаметр: D = мм
Поперечное сечение: круг диаметром d = мм
Число витков: n =
ПОЯСНЕНИЯ К РАБОТЕ
В различных машинах, механизмах, приборах пружины применяют для создания постоянных сил (тормоза, фрикционные передачи), в качестве элементов, смягчающих толчки и удары (амортизаторы, рессоры), для возврата движущихся деталей в исходное положение (клапанные пружины двигателей), для измерения величины силы (в динамометрах), в качестве устройств, аккумулирующих энергию (боевые пружины огнестрельного оружия), а также в элементах регистрирующих и записывающих приборов.
По форме винтовые пружины делятся на цилиндрические, конические и фасонные. Наиболее широко в технике применяются цилиндрические винтовые пружины, воспринимающие осевую нагрузку и работающие на растяжение (рис. 1а) или на сжатие (рис. 2а). Пружины растяжения навивают без просвета между витками, пружины сжатия – с просветом.
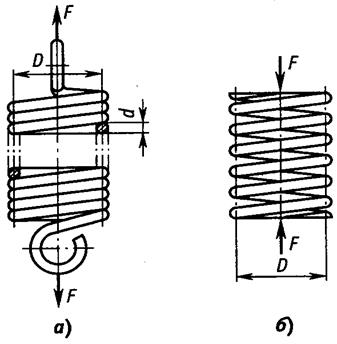
Рис. 1. Цилиндрические винтовые пружины:
а) – растяжения; б) – сжатия.
Пружины изготавливают из высококачественной стали марок 65Г, 65С, 60С2, имеющих высокие значения допускаемых касательных напряжений:
[t] = 200…1000 МПа
Для большинства пружин угол a наклона витков небольшой (a 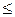 15º), поэтому для их расчета используется приближенная теория.
15º), поэтому для их расчета используется приближенная теория.
Расчет пружин растяжения и сжатия на прочность и жесткость одинаков, но для пружин сжатия при H: D 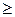 2,6 (H – высота пружины в свободном состоянии, D – ее средний диаметр) возникает опасность потери устойчивости (выпучивания). Такие высокие пружины монтируют в гильзах или на оправках, препятствующих выпучиванию пружин.
2,6 (H – высота пружины в свободном состоянии, D – ее средний диаметр) возникает опасность потери устойчивости (выпучивания). Такие высокие пружины монтируют в гильзах или на оправках, препятствующих выпучиванию пружин.
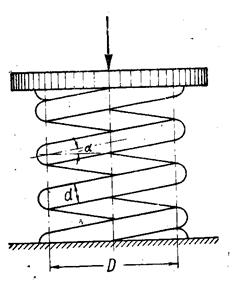
Рассмотрим пружину, нагруженную сжимающей силой F (рис. 2). Рассечем виток пружины (рис. 2а) плоскостью, проходящей через ее ось. Считая это сечение для витка поперечным, т.е. принимая a = 0 и рассматривая пружину как бы состоящую из колец, рассмотрим равновесие отсеченной части (рис. 2б).
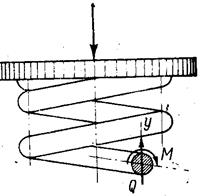 F F
F F
а) б)
Рис. 2
В сечении пружины возникают два внутренних силовых фактора:
поперечная сила
Q = F
и крутящий момент М = FD/2.
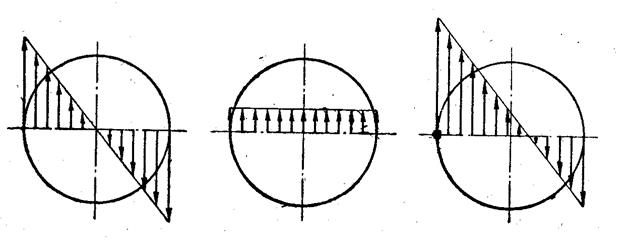
Касательные напряжения, связанные с наличием крутящего момента М, определяются так же, как при кручении бруса круглого поперечного сечения. Эпюра этих напряжений для точек диаметра витка показана на рис. 3а.
Касательные напряжения, связанные с наличием поперечной силы Q, распределены по сечению равномерно. Эпюра этих напряжений дана на рис. 3б.
Суммируя касательные напряжения, получаем результирующую эпюру, показанную на рис. 3в.
Опасной является точка А, ближайшая к оси пружины. Касательные напряжения в этой точке:
tА = tmax = maxtM + tQ (1)
maxtM
 tA
tA
tQ
О
О A О
а) б) в)
Рис. 3. Эпюры касательных напряжений в сечении витка пружины:
а) – от крутящего момента М = FD/2; б) – от поперечной силы Q = F;
в) – суммарная эпюра касательных напряжений.
Учитывая, что
maxtM = 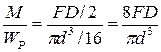
и tQ = 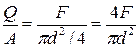 ,
,
получаем: tА = tmax = 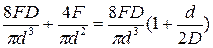 (2)
(2)
Отношение среднего диаметра пружины (D) к диаметру проволоки (d) называется индексом пружины и обозначается сп.
сп = D/d
Тогда tmax = 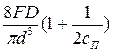 (3)
(3)
Обычно сп = 5…12. При указанных значениях сп второе слагаемое в скобках составляет не более 0,1 от первого. Если пренебречь вторым слагаемым, т.е. учитывать только напряжения кручения, получится приближенная формула:
tmax 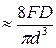 (4)
(4)
Формула (4) дает величину напряжений, меньшую действительной, т.к. в ней не учтено влияние поперечной силы и кривизна витков пружины. Исследования, выполненные методами теории упругости, позволяют уточнить значение tmax путем введения в формулу (4) поправочного коэффициента k, зависящего от индекса пружины и угла подъема витков. Его значение можно принимать по следующим данным:
| Индекс сп | ||||||
| Коэффициент k | 1,37 | 1,29 | 1,24 | 1,17 | 1,14 | 1,11 |
Несколько менее точное, но вполне приемлемое для практических расчетов значение k получается по формуле
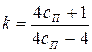
При более точных расчетах учитывают кривизну витков. Тогда значение поправочного коэффициента определяют по формуле
k ≈ 1 + 1,45/сп (5)
С учетом указанного коэффициента условие прочности пружины примет вид
tmax 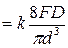 £ [t] (6)
£ [t] (6)
Для определения изменения высоты пружины под нагрузкой (у пружин сжатия эта величина называется осадкой и обозначается l) воспользуемся соотношениями. Работа внешней статически приложенной силы F определяется по теореме Клапейрона
W = 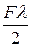 (7)
(7)
Эта работа равна энергии деформации пружины
 , (8)
, (8)
где G – модуль сдвига, JР – полярный момент инерции поперечного сечения витка.
В выражении (7) под длиной пружины ℓ понимается полная длина проволоки пружины ℓ ≈ πDn, где n – число рабочих витков пружины. Для пружин растяжения во внимание не принимается отогнутая часть витков. Для пружин сжатия из полного числа витков исключается примерно 3/4 витка с каждого торца, поскольку эти витки при навивке поджимаются к соседним и свободно деформироваться не могут. Таким образом предполагается, что 1,5 витка в работе не участвуют.
Приравнивая правые части выражений (6) и (7), получим:
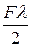 =
= 
Учитывая, что М = FD/2 и 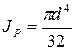 , имеем:
, имеем:
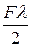 =
= 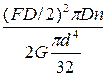 ,
,
откуда осадка пружины
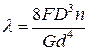 (9)
(9)
ЗАДАНИЕ
При подготовке к лабораторной работе студент должен:
– знать виды пружин и области их применения;
– знать внутренние силовые факторы, возникающие в поперечных сечениях витков пружины при приближенном расчете;
– знать основные параметры цилиндрических винтовых пружин;
– знать формулу для определения коэффициента k, учитывающего кривизну витков и напряжения среза;
– уметь строить эпюры касательных напряжений в сечениях витков;
– уметь определять напряжения в наиболее опасной точке витка;
– уметь определять осадку пружины;
– ответить на контрольные вопросы;
– правильно оформить отчет по лабораторной работе.
РАБОТА В ЛАБОРАТОРИИ
1. Установить пружину в приспособление для сжатия пружин.
2. Дать нагрузку F = H
3. Измерить величину осадки пружины l
4. Найти индекс пружины сп
5. Определить значение поправочного коэффициента k по формуле (5)
6. Рассчитать величину осадки lр пружины по формуле (9) и сравнить полученную величину с найденной экспериментально.
7. Вычислить значение наибольших касательных напряжений в витках пружины по формуле (6) и сравнить их с допускаемыми [t] = 300 МПа
8. Сделать выводы.
РЕЗУЛЬТАТЫ РАБОТЫ
Расчетные формулы
1. Индекс пружины cп = 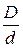 =
=
2. Поправочный коэффициент, учитывающий индекс пружины и кривизну витков k = 1 + 1,45/ cп = 1 + 1,45/ =
3. Расчетное значение осадки пружины
lP = 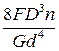 =
=
4. Значение наибольших касательных напряжений в точке А приужины
tA = 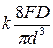 =
=
ТАБЛИЦА РЕЗУЛЬТАТОВ
| D, мм | d, мм | n | F, Н | l, мм | cп | k | lP, мм | tA, МПа |
В Ы В О Д Ы
1. Величины осадки пружины, определенные опытным и расчетным путем, оказались примерно одинаковыми. Значит, формула (9) верна.
2. Значения максимальных касательных напряжений в точках, находящихся ближе к центру, не превысили допускаемых. Значит, условие прочности пружины не нарушено.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какая деталь называется пружиной?
2. Назовите типы пружин и области их применения.
3. Из какого металла изготавливают пружины?
4. Чем отличаются пружины сжатия от пружин растяжения?
5. Какое число витков у пружин растяжения и сжатия исключается при расчете и почему?
6. Что такое индекс цилиндрической винтовой пружины и каково его значение?
7. На какой вид деформации работают витки пружины?
8. В чем заключается приближенный расчет пружин?
9. По каким формулам вычисляется поправочный коэффициент k, учитывающий индекс пружины сп, влияние поперечной силы Q и угол α наклона витков?
10. Что такое осадка l пружины и по какой формуле она вычисляется?
Л И Т Е Р А Т У Р А
1. Агамиров Л.В. Сопротивление материалов. Краткий курс. М.: ООО «Издательство Астрель»: ООО «Издательство АСТ», 2003.– 256 с.: ил.
2. Анурьев В.И. Справочник конструктора-машиностроителя, том 1. М.: «Машиностроение», 1979. – 728 с.: ил.
3. Бородин Н.А. Сопротивление материалов: Пособие для студентов ссузов. М.: Дрофа, 2001. – 288 с.: ил.
4. Ивченко В.А. Техническая механика: Учебное пособие. – М.: ИНФРА-М, 2003. – 157 с.
5. Ицкович Г.М. Сопротивление материалов. М.; «Высшая школа», 1970. – 488 с.: ил.
6. Олофинская В.П. Техническая механика: Курс лекций с вариантами практических и тестовых заданий: Учебное пособие. – М.: ФОРУМ: ИНФРА-М, 2003. – 349 с., ил.
7. Эрдеди А.А., Эрдеди Н.А. Теоретическая механика. Сопротивление материалов: М.: Высш. шк., 2002. – 318 с.: ил.
Date: 2015-07-27; view: 2198; Нарушение авторских прав