Ограничения многочленной интерполяции

Многочленная интерполяционная функция очень чувствительна к выбору узлов интерполяции.

Рассмотрим интерполяционную формулу Лагранжа

,

где

.

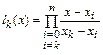Оценим норму функции 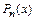, которую определим, как

.

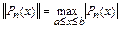С этой целью выполним очевидные преобразования:

.

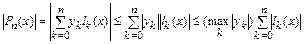Введем функцию Лебега:

.

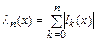Поскольку 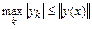, получаем оценку:

.

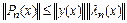Величина нормы функции 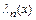зависит от распределения узлов интерполяции. Рассмотрим два случая.

Случай 1. Узлы интерполяции 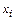на отрезке 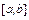распределены равномерно. В этом случае 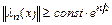(доказательство опускаем). При увеличении n многочлен 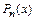может полностью оказаться непригодным для аппроксимации 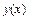, т. к. 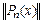неограниченно возрастает.

Рассмотрим такой пример. Будем интерполировать функцию

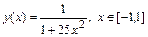
полиномом n -го порядка, выбирая узлы интерполяции равномерно распределенными. Введем норму ошибки интерполяции:

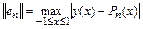
и исследуем ее зависимость от порядка интерполирующего полинома. Для этого обратимся к численным результатам (см. табл.8.1).

Таблица 8.1

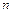
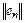
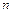
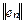
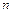
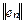
	0.96		0.25		1.07
	0.71		0.30		2.10
	0.43		0.56		4.21

Видно, что с увеличением 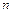погрешность интерполяции уменьшается вплоть до 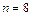. Дальнейшее увеличение порядка полинома приводит к возрастанию .

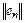Случай 2. Узлы интерполяции являются нулями полинома Чебышева. Их нетрудно получить, если на отрезке 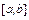построить полуокружность, разделить ее на 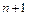равные части и спроектировать на отрезок середину каждой из них (рис. 8.1). В этом случае 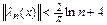(доказательство опускаем). Обратимся к рассмотренному выше примеру (см. табл.8.2) Погрешность интерполяции теперь при возрастании порядка полинома монотонно падает.

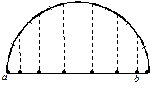
Рис. 8.1. Расположение нулей полинома Чебышева

Таблица 8.2

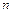
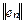
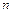
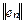
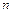
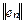
	0.93		0.39		0.12
	0.75		0.27		0.08
	0.56		0.18		0.06

Многочленная интерполяция в точках Чебышева позволяет увеличивать точность приближения функции посредством увеличения порядка полинома. Однако привлекать узлы Чебышева не всегда удается. (Например, в узле Чебышева функция имеет особенность.) Чтобы избежать зависимости точности аппроксимации от локальных свойств функции, переходят к кусочно-полиномиальной аппроксимации.

Date: 2015-07-27; view: 503; Нарушение авторских прав